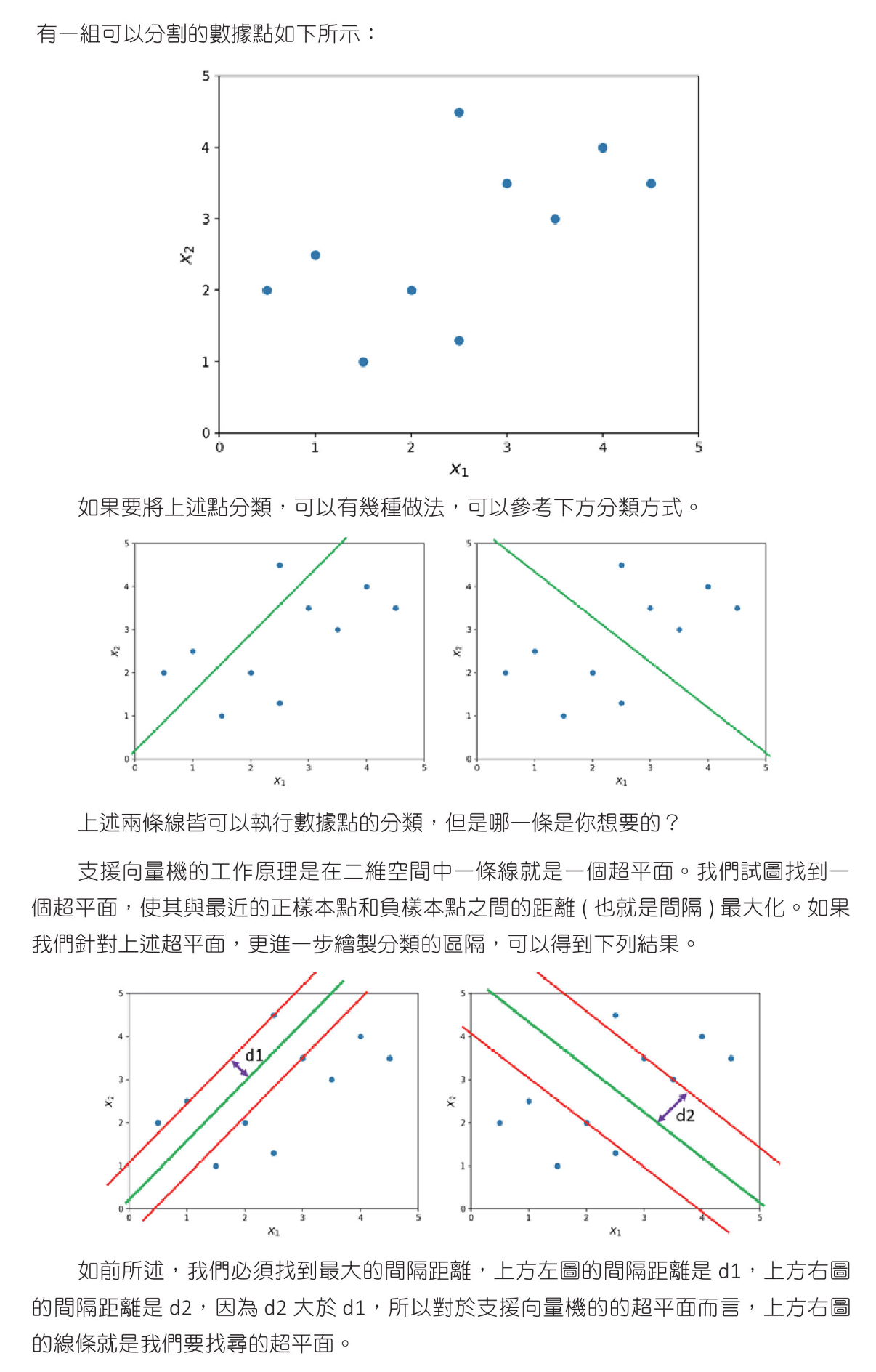
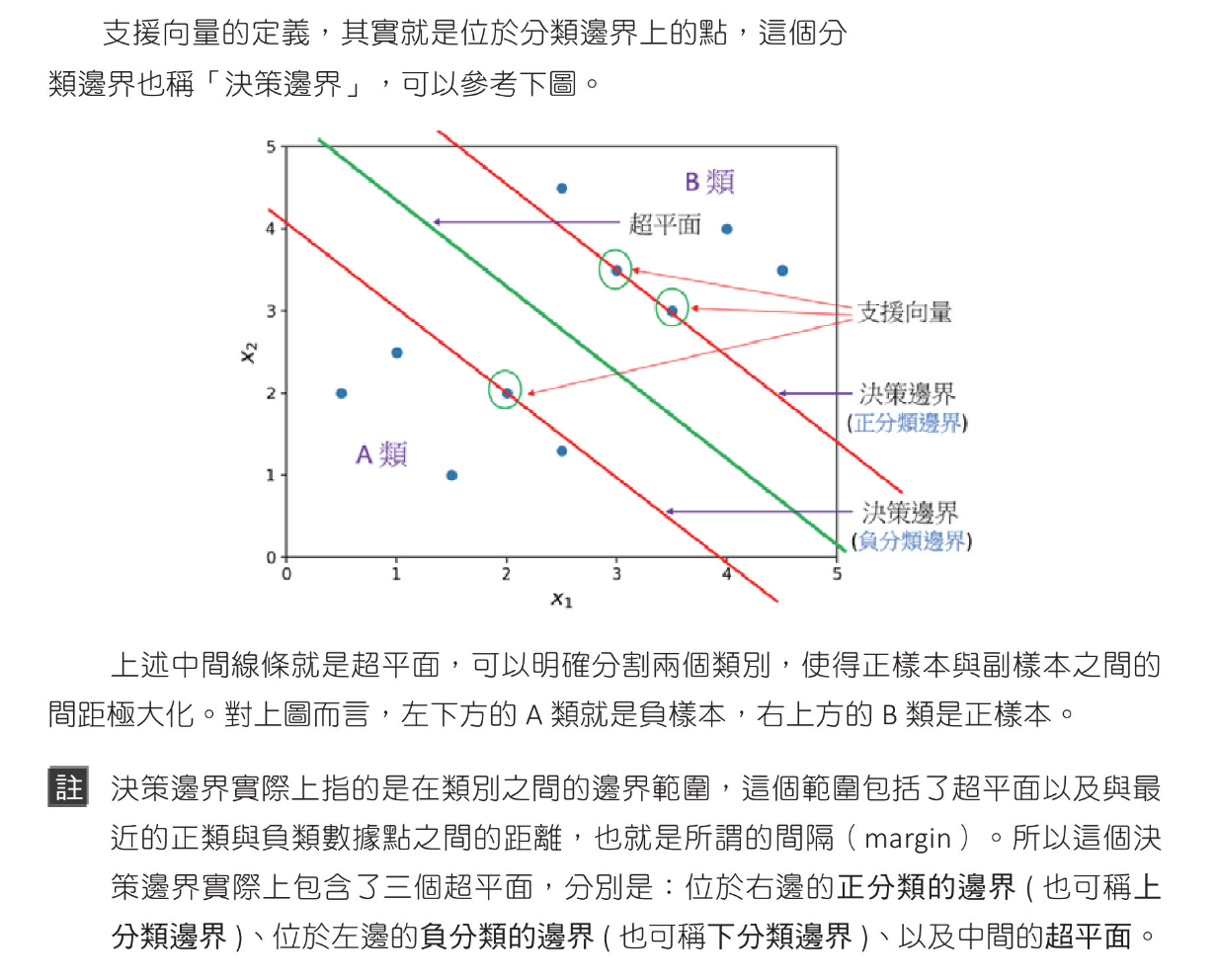
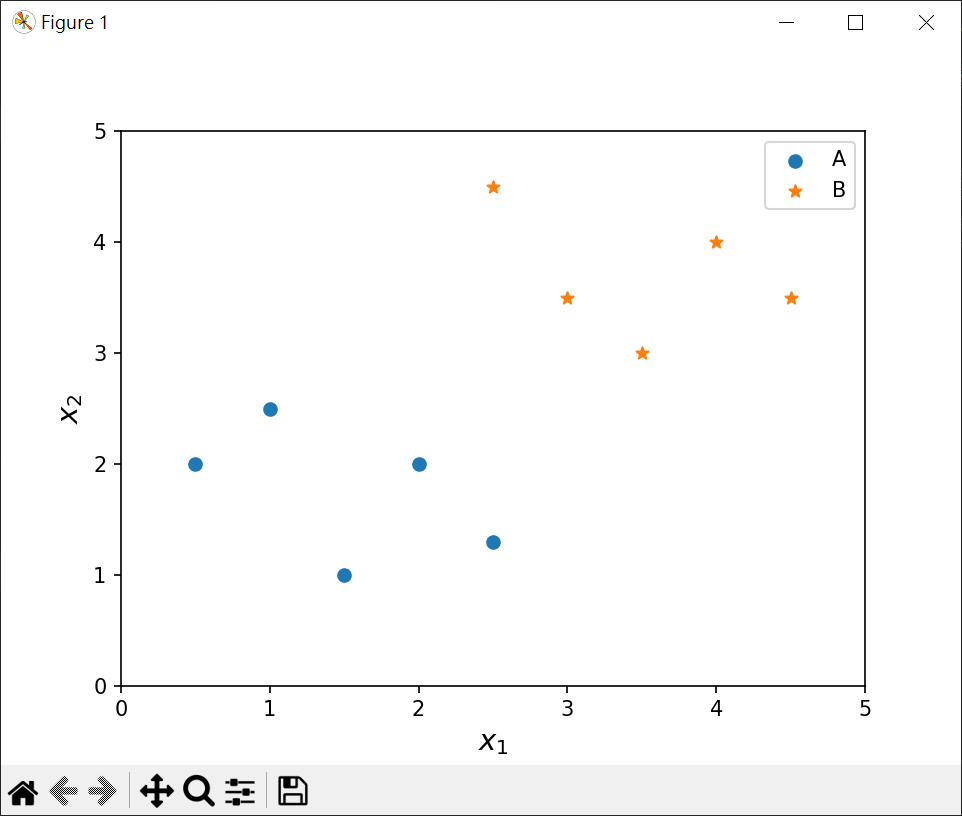
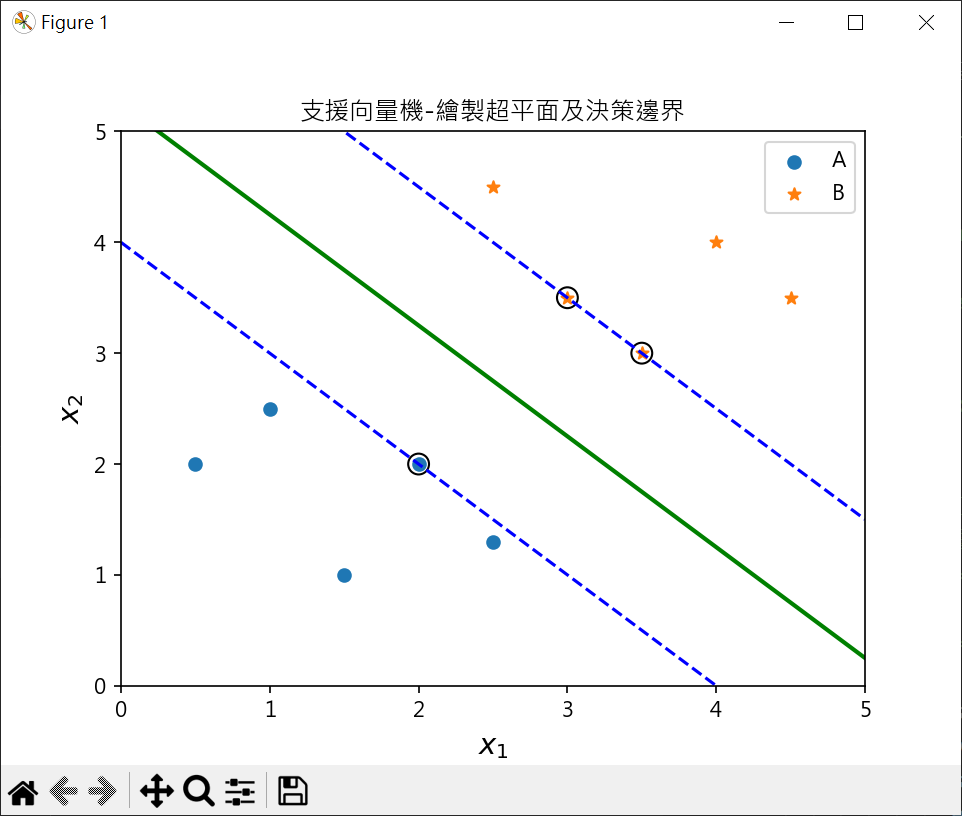
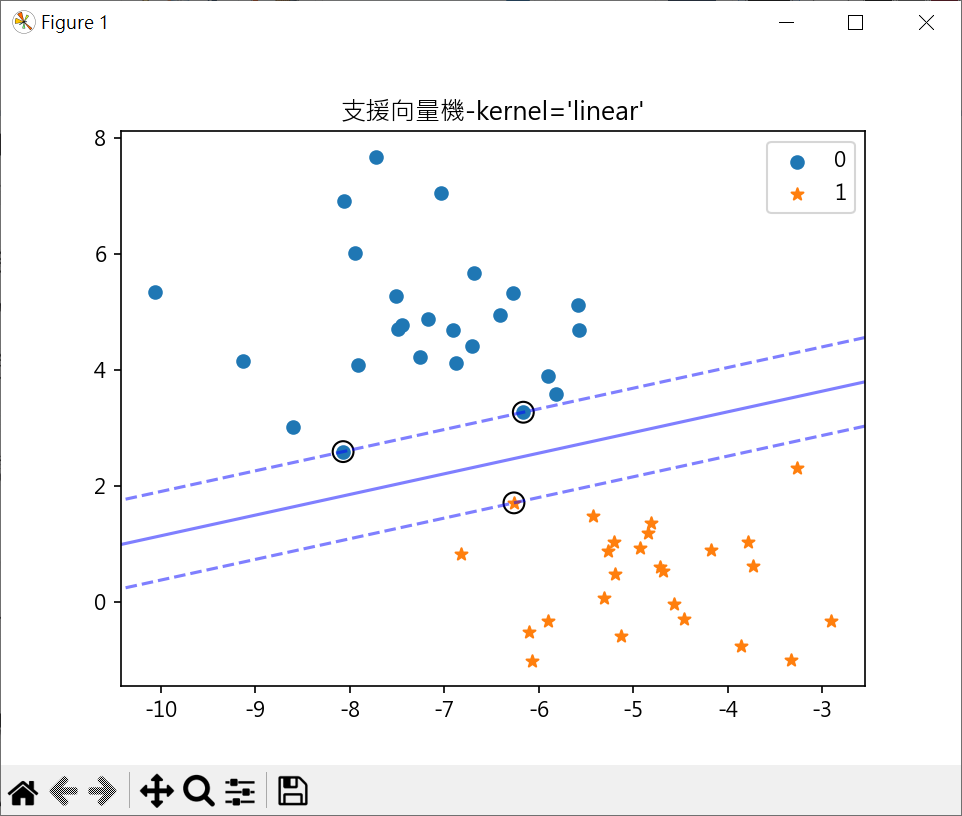
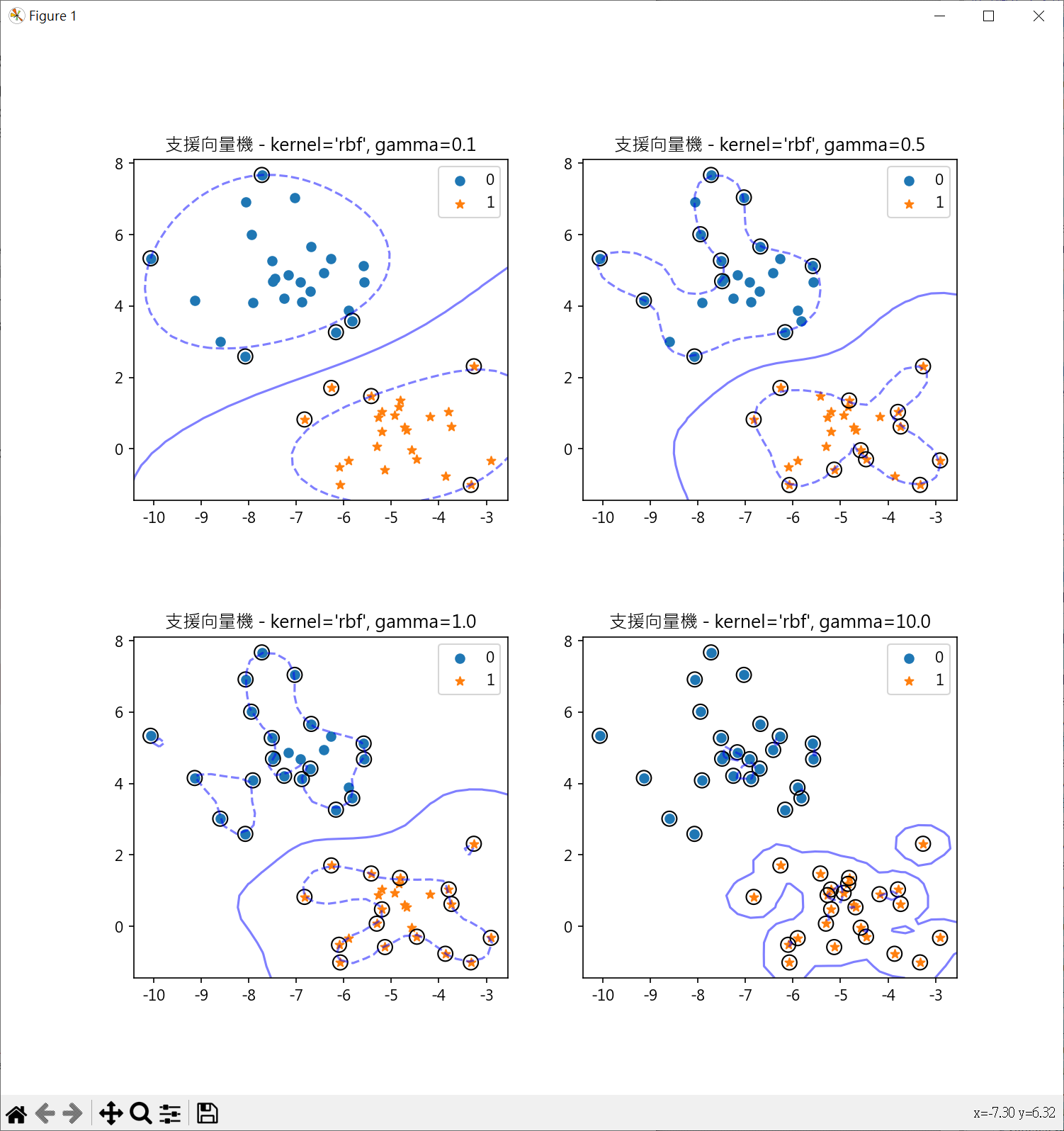
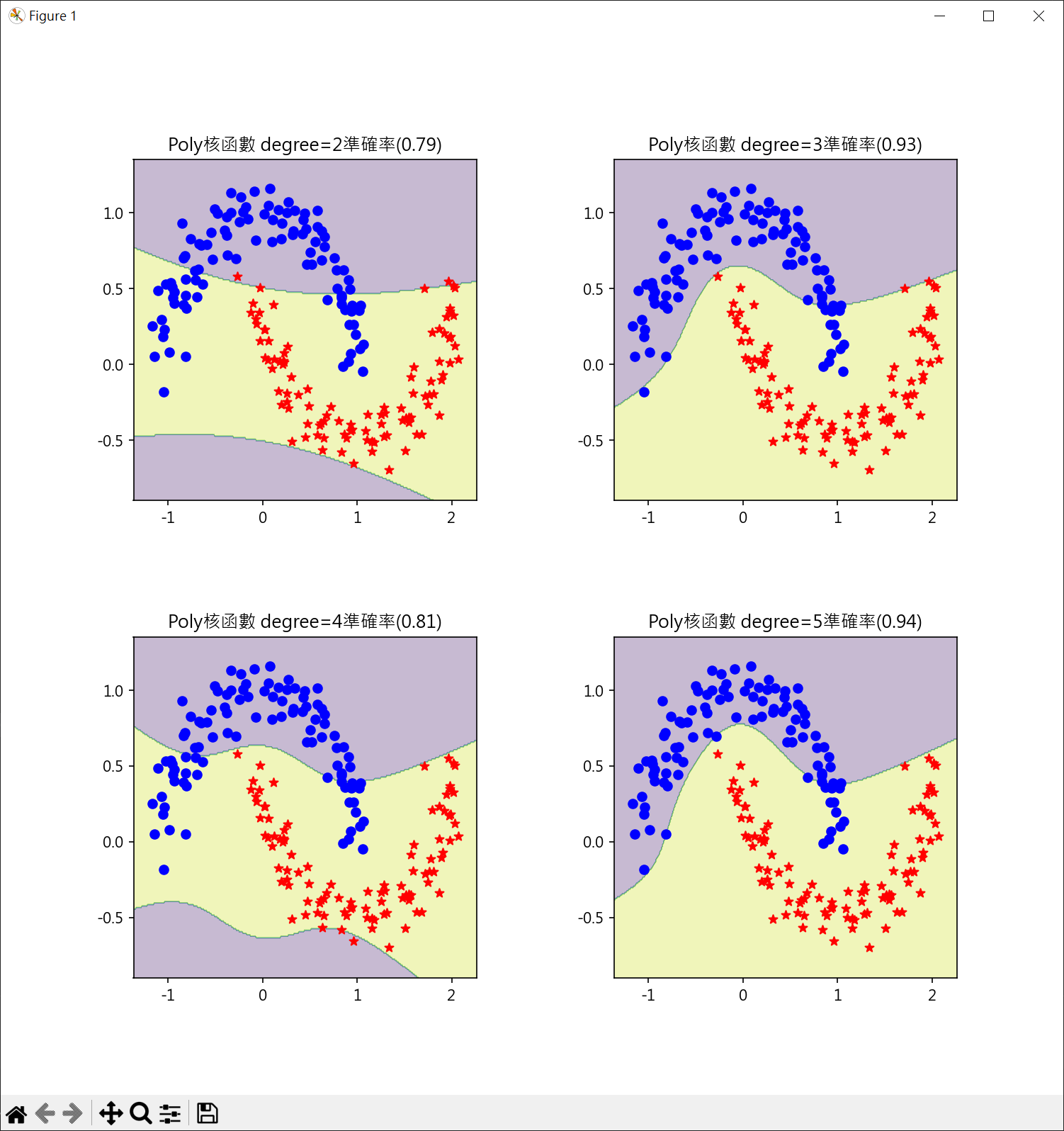
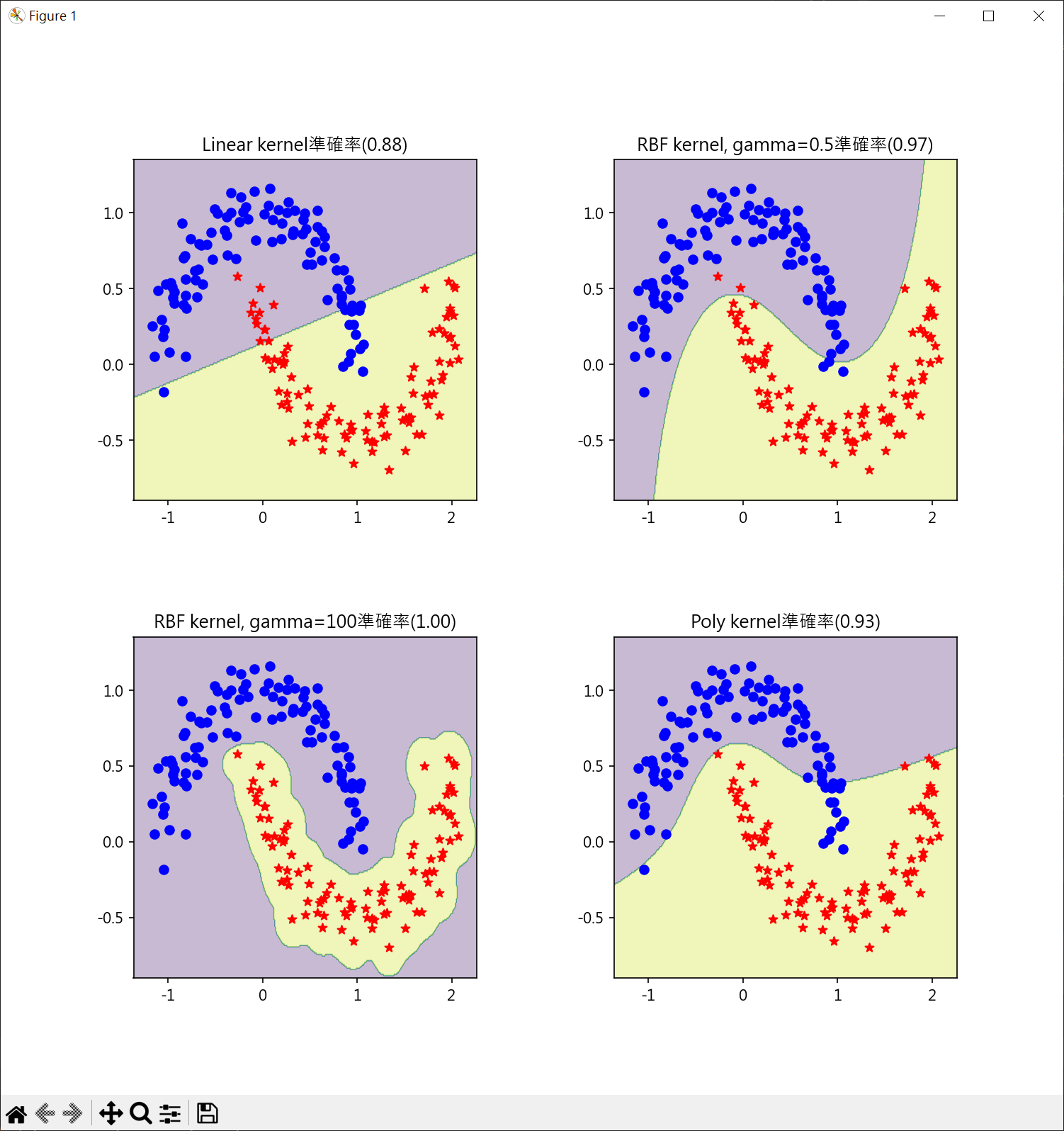
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
|
import numpy as np
from sklearn import svm
import matplotlib.pyplot as plt
from joblib import dump
plt.rcParams["font.family"] = ["Microsoft JhengHei"]
X = np.array([[1, 2.5], [0.5, 2], [2, 2], [1.5, 1], [2.5, 1.3],
[3, 3.5], [4.5, 3.5], [4, 4], [2.5, 4.5], [3.5, 3] ])
y = np.array(['A','A','A','A','A','B','B','B','B','B',])
svc = svm.SVC(kernel='linear')
svc.fit(X, y)
for i, marker in zip(['A', 'B'], ['o', '*']):
plt.scatter(X[y==i, 0], X[y==i, 1], marker=marker, label=i )
ax = plt.gca()
xx = np.linspace(0, 5)
yy = np.linspace(0, 5)
XX, YY = np.meshgrid(xx, yy)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = svc.decision_function(xy).reshape(XX.shape)
ax.contour(XX, YY, Z, colors='b', levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])
plt.scatter(svc.support_vectors_[:,0], svc.support_vectors_[:,1],
s=100, facecolors='none', edgecolors='k')
plt.title('支援向量機-繪製超平面及決策邊界')
plt.xlabel(r'$x_{1}$', fontsize=14)
plt.ylabel(r'$x_{2}$', fontsize=14)
plt.legend()
plt.show()
|