scikit-learn

發表於 更新於 分類於 Disqus：
文章字數： 27k 所需閱讀時間 ≈ 25 分鐘

基本

  • scikit-learn 是一個開源的 python 機器學習庫,提供一系列監督及非監督學習算法
  • 提供大量用於分類,迴歸,群集,降維,模型選擇和預處理工具
  • 廣泛運用於數據挖掘和數據分析

install

1
pip install scikit-learn

評估模型

均方誤差(Mean Square Error, MSE)

MSE是觀察值與預測值之間差值平方的平均值,MSE越小,表示模型的預測能力越好,公式如下
$ MSE = \frac{1}{n} \sum_{i-1}^{n}(y_i-\hat{y})$
$ y_i是觀察值 \hat{y}是預測值 n是樣本數量 $

1
2
3
from sklearn.metrics import mean_squared_error
	...
MSE = mean_squared_error(y_true, y_pred)
均方根誤差(Root Mean Square Error, RMSE)

這是MSE的平方根,與MSE相比,RMSE對較大的誤差有更強的懲罰效果
RMSE = np.sqrt(MSE)

平均絕對誤差(Mean Absolute Error, MAE)

這是預測值與實際值之間的絕對差平均值,這個指標能夠更好的反映預測誤差的實際大小

1
2
3
from sklearn.metrics import mean_absolute_error
	...
MAE = mean_absolute_error(y_true, y_pred)
R平方判定係數(Coefficient of Determination RMSE)

R平方判定係數或簡稱判定係數,是一個迴歸模型性能評估指標,用於衡量模型資料變異程度.值介於0~1,越接近1表示模型對資料的擬合程度越好.

$ Adjusted R^2 = 1 - \frac{(1-R^2)*(n-1)}{(n-k-1)} $
$ n表示樣品數量,k表示特徵數量,R^2表示判定係數 $

判定係數公式如下:
$$ R^2(y,\hat{y}) = 1 - \frac{\sum_{i=1}^{n}(y_i - \hat{y}_i)^2} { \sum _{i=1}^{n}(y_i - \overline{y})^2 } $$

$ n 是數據量, \hat{y}_i 是迴歸函數的預估值,\overline{y} 是所有y的平均值 $

1
2
3
from sklearn.metrics import r2_score
	...
R2_score = r2_score(y_true, y_pred)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from sklearn.metrics import r2_score, mean_squared_error
import numpy as np

x = [ 1, 2, 3, 4, 5, 6, 7, 8, 9,10,11,
     12,13,14,15,16,17,19,21,22,23,24]
y = [100, 88, 75, 60, 50, 55, 55, 56, 58, 58, 61,
      63, 68, 71, 71, 75, 76, 88, 93, 97, 97, 100]

coef = np.polyfit(x, y, 3)
model = np.poly1d(coef)
print(f"MSE:{mean_squared_error(y, model(x)):.3f}")
print(f"R2_Score:{r2_score(y, model(x)):.3f}")
# MSE:14.803
# R2_Score:0.944

機器學習數據集

可使用以下數據集作為機器學習使用

scikit-learn 內建數據集

scikit-learn 提供一些數據集

  • 鳶尾花 Iris
  • 手寫數字 Digits
  • 葡萄酒 Wine
  • 威斯康辛州乳癌 Breast Cancer Wisconsin
  • 波士頓房價 Boston House Prices
Kaggle 數據集
  • Kaggle 是一個數據科學平台
  • 數據涵蓋許多不同主題,包含但不限於金融,醫療,影像識別,自然語言處理,音訊分析
  • Kaggle 有活躍的社區,你可以參加由Kaggle或其他機構主辦的數據科學競賽,並可以查看其他使用者對數據集的分析和模型
  • 對每個數據集,可以找到相關的核心筆記本(kernels),討論和新聞,這些可幫助使用者理解和使用數據集
    為了使用 Kaggle 數據集,需註冊一個帳號,你可以直接下載或使用API下載
UCI 數據集
  • UCI 數據集由加州大學爾灣分校(University of California, Irvine)機器學習儲存庫提供
  • 涵蓋醫學,金融,生物學和社會科學等
  • 這些數據涉及的領域包含機器學習,統計學,模式識別,數據挖掘等
  • 可用於機器學習任務,如分類,迴歸,聚類等
    UC Irvine Machine Learning Repository
函數生成數據集(scikit-learn 函數生成數據)

也可以使用 scikit-learn 內建的函數生成下列類型的數據集:

  • 線性分佈數據集
  • 集群分佈數據集
  • 循環分佈數據集

scikit-learn 生成數據實作

線性分佈數據
1
2
3
from sklearn.datasets import make_regression
	...
X, y = make_regression(n_samples, n_features, noise, random_state)
  • n_samples : options,生成樣品數量, default 100
  • n_features : options,生成特徵數量, default 100
  • noise : option,加入高斯噪聲的標準差, default 0
  • random_state : option,隨機生成器的種子,加入此參數確保每次生成數據一致, default None(每次生成數據不同)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
# 產生數據
from sklearn.datasets import make_regression

X, y = make_regression(n_features=1, noise=0, random_state=0)
print("X 的資料格式:")
print(type(X), len(X))
print(f"陣列維度:{X.ndim}")
print(f"陣列外型:{X.shape}")
print(f"陣列大小:{X.size}")
print(f"前5個X的樣本:")
print(X[:5])
print("="*70)

print("y 的資料格式:")
print(type(y), len(y))
print(f"陣列維度:{y.ndim}")
print(f"陣列外型:{y.shape}")
print(f"陣列大小:{y.size}")
print(f"前5個y的樣本:")
print(y[:5])

# X 的資料格式:
# <class 'numpy.ndarray'> 100
# 陣列維度:2
# 陣列外型:(100, 1)
# 陣列大小:100
# 前5個X的樣本:
# X 為 2維 陣列
# [[ 0.12691209]
#  [ 0.44386323]
#  [ 0.76103773]
#  [ 0.95008842]
#  [-0.40317695]]
# ======================================================================
# y 的資料格式:
# <class 'numpy.ndarray'> 100
# 陣列維度:1
# 陣列外型:(100,)
# 陣列大小:100
# 前5個y的樣本:
# y 為 2維 陣列
# [  5.37923312  18.81336721  32.25696819  40.26997723 -17.08885844]
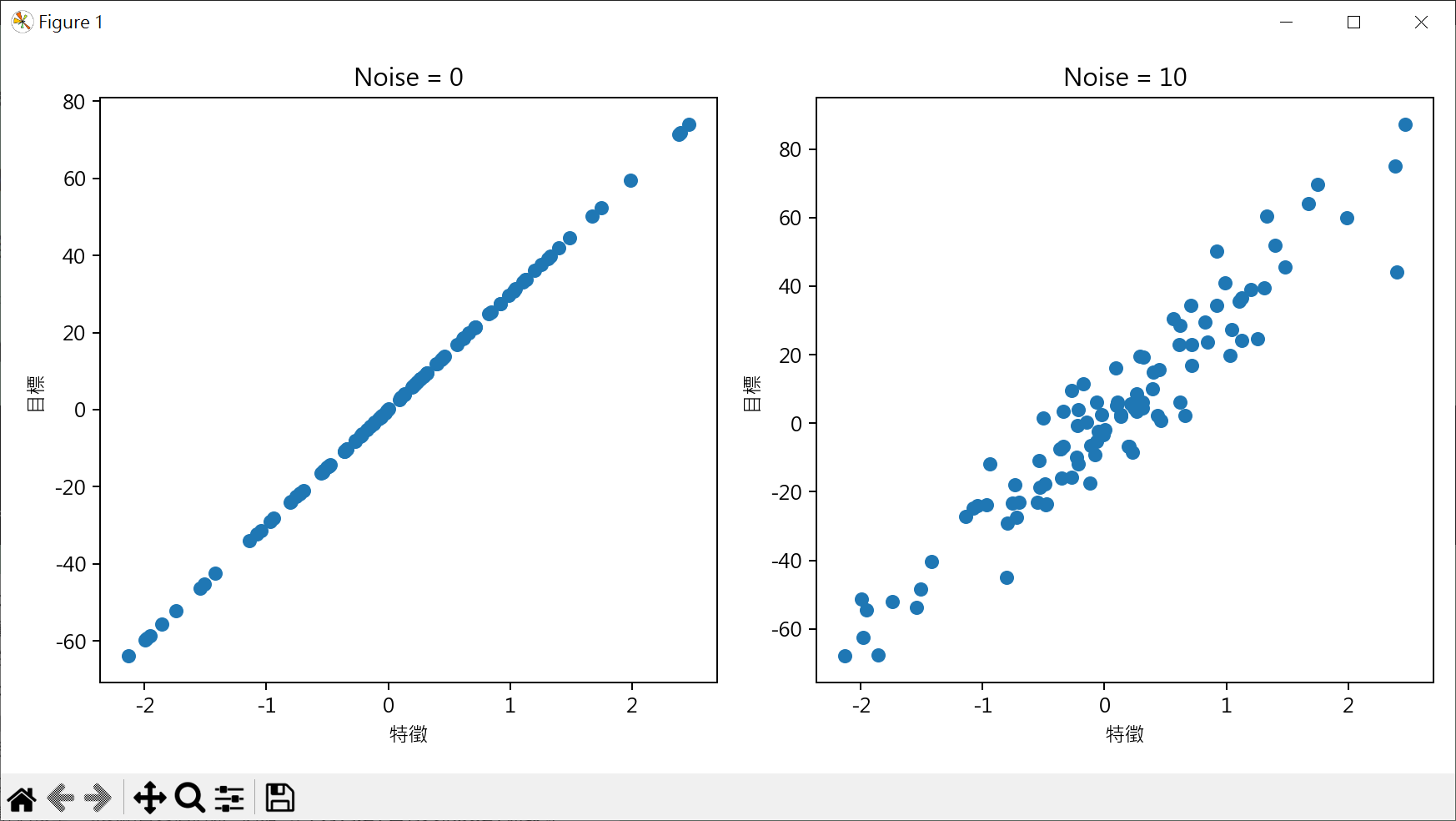
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 對照兩組數據
# 繪製多子圖
from sklearn.datasets import make_regression
import matplotlib.pyplot as plt

# windows 使用 微軟正黑體
plt.rcParams["font.family"] = ["Microsoft JhengHei"]
# 顯示負號
plt.rcParams["axes.unicode_minus"] = False

# 生成數據
X1, y1 = make_regression(n_features=1, noise=0, random_state=10)
X2, y2 = make_regression(n_features=1, noise=10, random_state=10)

# 建立兩個子圖畫布
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10,5))
# 繪第1個子圖
axs[0].scatter(X1, y1)
axs[0].set_title("Noise = 0")
# 繪第2個子圖
axs[1].scatter(X2, y2)
axs[1].set_title("Noise = 10")
# 設定標籤
for ax in axs:
    ax.set_xlabel("特徵")
    ax.set_ylabel("目標")

# 自動調整子圖間距
plt.tight_layout()
plt.show()
群集分佈數據
1
2
3
from sklearn.datasets import make_blobs
	...
X,y = make_blobs(n_samples, n_features, centers, random_state)
  • n_samples : options,生成樣品數量, default 100
  • n_features : options,每個樣品特徵數, default 2
  • centers : option,整數或是一組[n_cneters, n_feature]的陣列,表示生成數據中心數量或固定中心位置, default 3
  • random_state : option,隨機生成器的種子,加入此參數確保每次生成數據一致, default None(每次生成數據不同)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
from sklearn.datasets import make_blobs

X,y = make_blobs(n_samples=500, n_features=2, centers=5, random_state=1)
print(f"輸出 X 的資料格式:")
print(type(X))
print(f"X 前 5 個樣本")
print(X[:5])
print("="*70)

print(f"X[:,0] 前 5 個樣本")
xx = X[:,0]
print(xx[:5])
print("="*70)

print(f"X[:,1] 前 5 個樣本")
xx = X[:,1]
print(xx[:5])
print("="*70)

print(f"y 前 5 個樣本")
print(y[:5])
# 輸出 X 的資料格式:
# <class 'numpy.ndarray'>
# X 前 5 個樣本
#  n_features=2 所以每個樣本有 2 個特徵
# [[-2.33022219  4.78405366]
#  [-2.27930436  1.79758281]
#  [-7.22570502 -3.79313579]
#  [-7.66603898 -7.59715459]
#  [-7.83173733 -3.70122759]]
# ======================================================================
# X[:,0] 前 5 個樣本
# [-2.33022219 -2.27930436 -7.22570502 -7.66603898 -7.83173733]
# ======================================================================
# X[:,1] 前 5 個樣本
# [ 4.78405366  1.79758281 -3.79313579 -7.59715459 -3.70122759]
# ======================================================================
# y 前 5 個樣本
# [0 4 3 2 3]
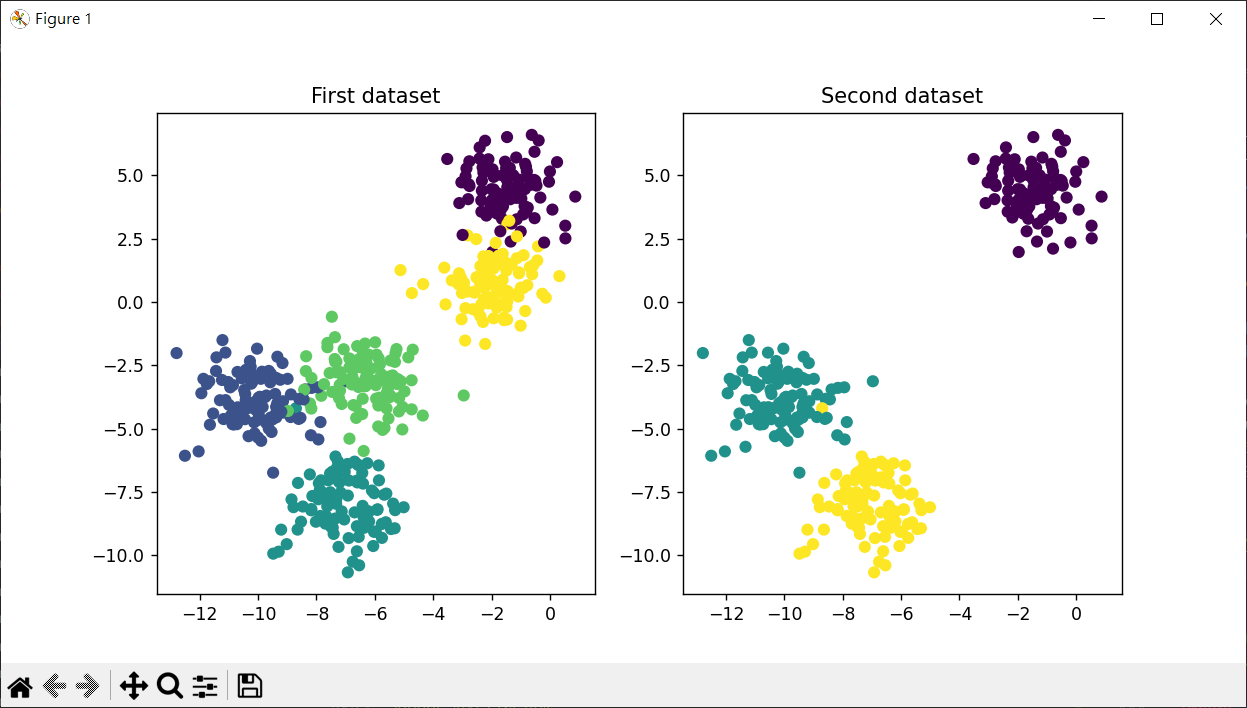
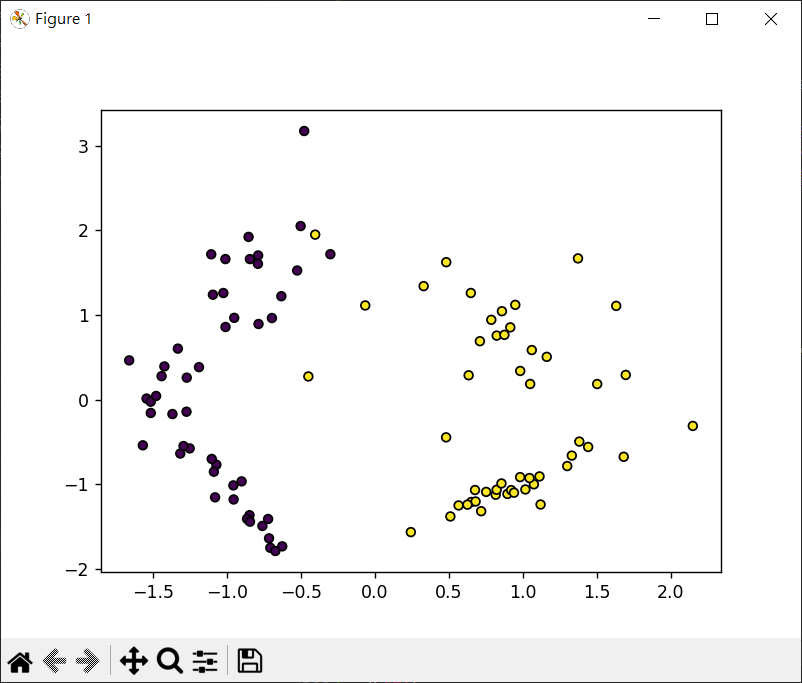
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from sklearn.datasets import make_blobs
import matplotlib.pylab as plt

X1 ,y1 = make_blobs(n_samples=500, n_features=2, centers=5, random_state=1)
X2 ,y2 = make_blobs(n_samples=300, n_features=2, centers=3, random_state=1)

# 建立兩個子圖畫布
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10,5))
# 繪第1個子圖
axs[0].scatter(X1[:,0], X1[:,1], c=y1)
axs[0].set_title("First dataset")
# 繪第2個子圖
axs[1].scatter(X2[:,0], X2[:,1], c=y2)
axs[1].set_title("Second dataset")

plt.show()
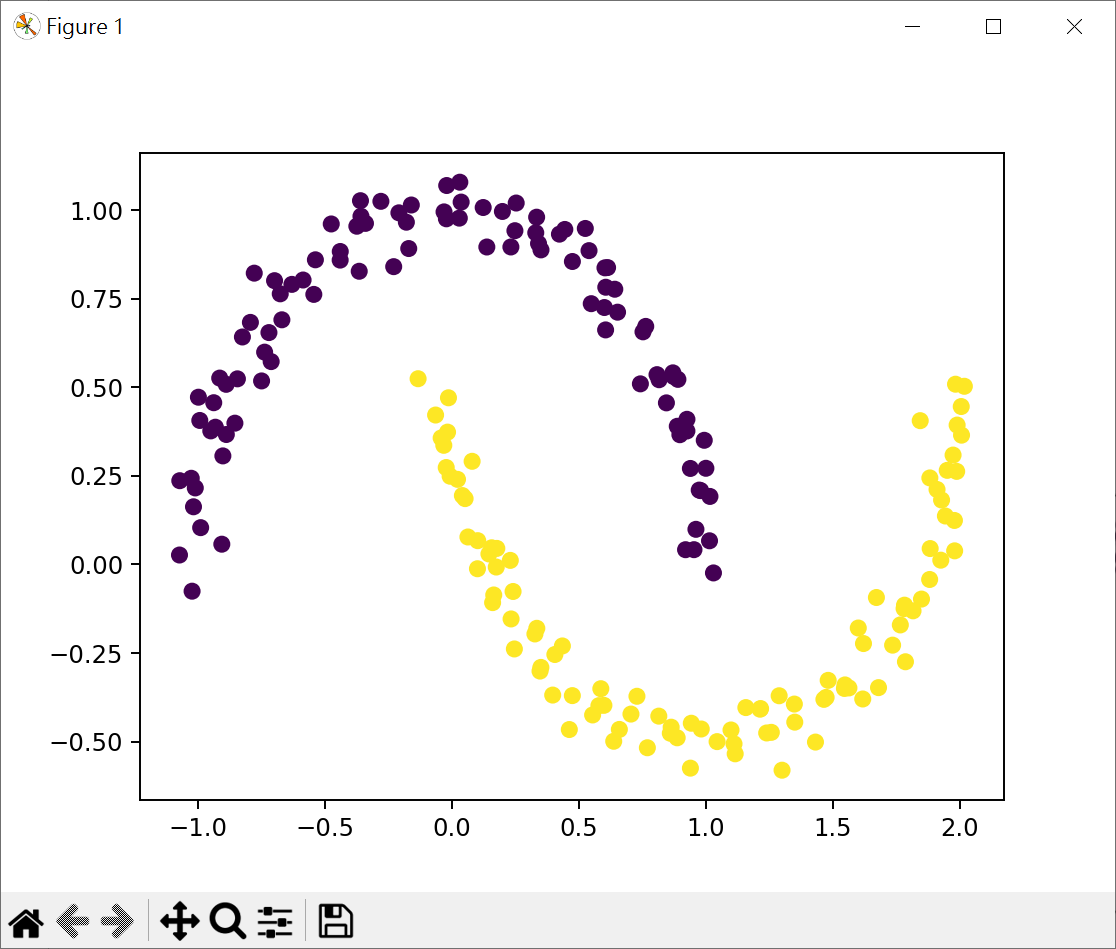
交錯半月群集數據

玩具數據集通常指那些簡單,小型的人造數據集
make_moons 就是一個玩具數據集的例子,數據集的兩個類別會在二維空間中形成兩個交錯的半圓形

1
2
3
from sklearn.datasets import make_moons
	...
X, y = make_moons(n_samples, noise, random_state)
  • n_samples : options,生成樣品數量, default 100
  • noise : option,加入高斯噪聲的標準差, default None
  • random_state : option,隨機生成器的種子,加入此參數確保每次生成數據一致, default None(每次生成數據不同)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from sklearn.datasets import make_moons
import matplotlib.pyplot as plt

X, y = make_moons(n_samples=200, noise=0.05, random_state=0)

print(f"X[:5] = {X[:5]}")
print(f"y={y}")

plt.scatter(X[:,0], X[:,1], c=y)
plt.show()

# X[:5] = [[ 0.81680544  0.5216447 ]
#  [ 1.61859642 -0.37982927]
#  [-0.02126953  0.27372826]
#  [-1.02181041 -0.07543984]
#  [ 1.76654633 -0.17069874]]
# y=[0 1 1 0 1 1 0 1 0 1 0 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 1 1 1 0 0 0 1 1 0 1 1
#  0 0 1 1 0 0 1 1 0 0 0 1 1 0 1 1 0 1 0 0 1 0 0 1 0 1 0 1 0 0 1 0 0 1 0 1 1
#  1 0 1 0 0 1 1 0 1 1 1 0 0 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 0 0 0 1 0 0 1 0 0
#  0 0 0 0 1 0 1 1 0 0 0 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 1 0 1 1 0 0 0 0 1 1
#  0 1 1 1 0 0 1 0 1 1 0 0 1 1 0 1 1 1 0 1 1 1 0 0 0 0 1 1 1 0 0 0 1 0 1 1 1
#  0 0 1 0 0 0 0 0 0 1 0 1 1 0 1]
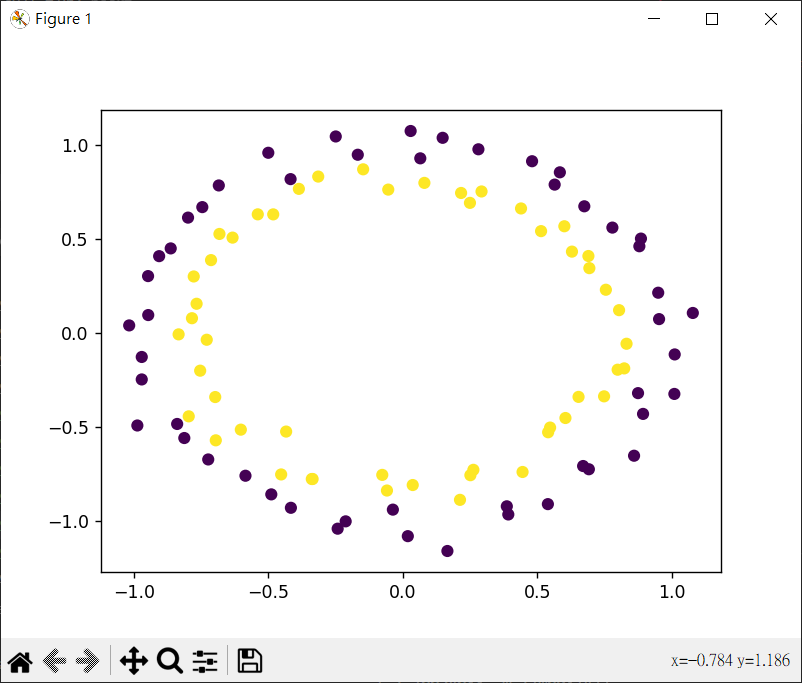
環形結構分佈的群集數據

make_circles() 可以用來生成兩個環狀結構的數據集,一個圓內部的點和一個圓外部的點

1
2
3
from sklearn.datasets import make_circles
	...
X, y = make_circles(n_samples, noise, random_state)
  • n_samples : options,生成樣品數量, default 100
  • noise : option,加入高斯噪聲的標準差, default None
  • random_state : option,隨機生成器的種子,加入此參數確保每次生成數據一致, default None(每次生成數據不同)
1
2
3
4
5
6
7
from sklearn.datasets import make_circles
import matplotlib.pyplot as plt

X, y = make_circles(n_samples=100, noise=0.05, random_state=0)

plt.scatter(X[:,0],  X[:,1], c=y)
plt.show()
n-class 分類數據集
1
2
3
from sklearn.datasets import make_classification
	...
X, y = make_classification(n_samples=100, n_features=20, n_informative=2, n_redundant=2, n_repeated=0, n_classes=2,  n_clusters_per_class=2, weights=None, hypercube=True, shift=0.0, scale=1.0, shuffle=True, random_state=None)
  • n_samples : options,生成樣品數量, default 100
  • n_features : options,生成特徵數量, default 20
  • n_informative : 信息特徵數, default 2
  • n_redundant : 冗餘特徵數, default 1
  • n_repeated : 重複特徵數, default 0
  • n_classes : 數據集中類別數, default 2
  • n_clusters_per_class : 每個類別的簇數, default 2
  • weights : 每個類別樣品所佔的比例, default None
  • hypercube : 如為 True 將簇放置在超立方體的頂點上, 如為 False 將簇放置在隨機多維標準常規中, default True
  • shift : 特徵的均值, default 0.0
  • scale : 特徵的標準差, default 1.0
  • random_state : option,隨機生成器的種子,加入此參數確保每次生成數據一致, default None(每次生成數據不同)
1
2
3
4
5
6
7
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt

X, y = make_classification(n_samples=100, n_features=2, n_informative=2, n_redundant=0, n_repeated=0, n_classes=2, random_state=1)

plt.scatter(X[:,0], X[:,1], marker='o', c=y, s=25, edgecolors='k' )
plt.show()

scikit-learn 數據預處理

scikit-learn 數據預處理 有以下幾點

  • 數據清洗:消除數據中的噪聲,例如遺漏值,異常值或不一致的數據等
  • 數據轉換:將數據轉換成適合模型學習的格式.如某些算法只能處理數值數據,所以我們需要將類別數據進行編碼
  • 數據標準化/正規化:消除數據尺度的差異,讓所有的特徵都在尺度範圍內(數據標準化也稱為數據縮放)
  • 特徵選擇/提取:有時我們要減少數據的維度以減少運算,或者將原始特徵轉換成更好表示數據的新特徵
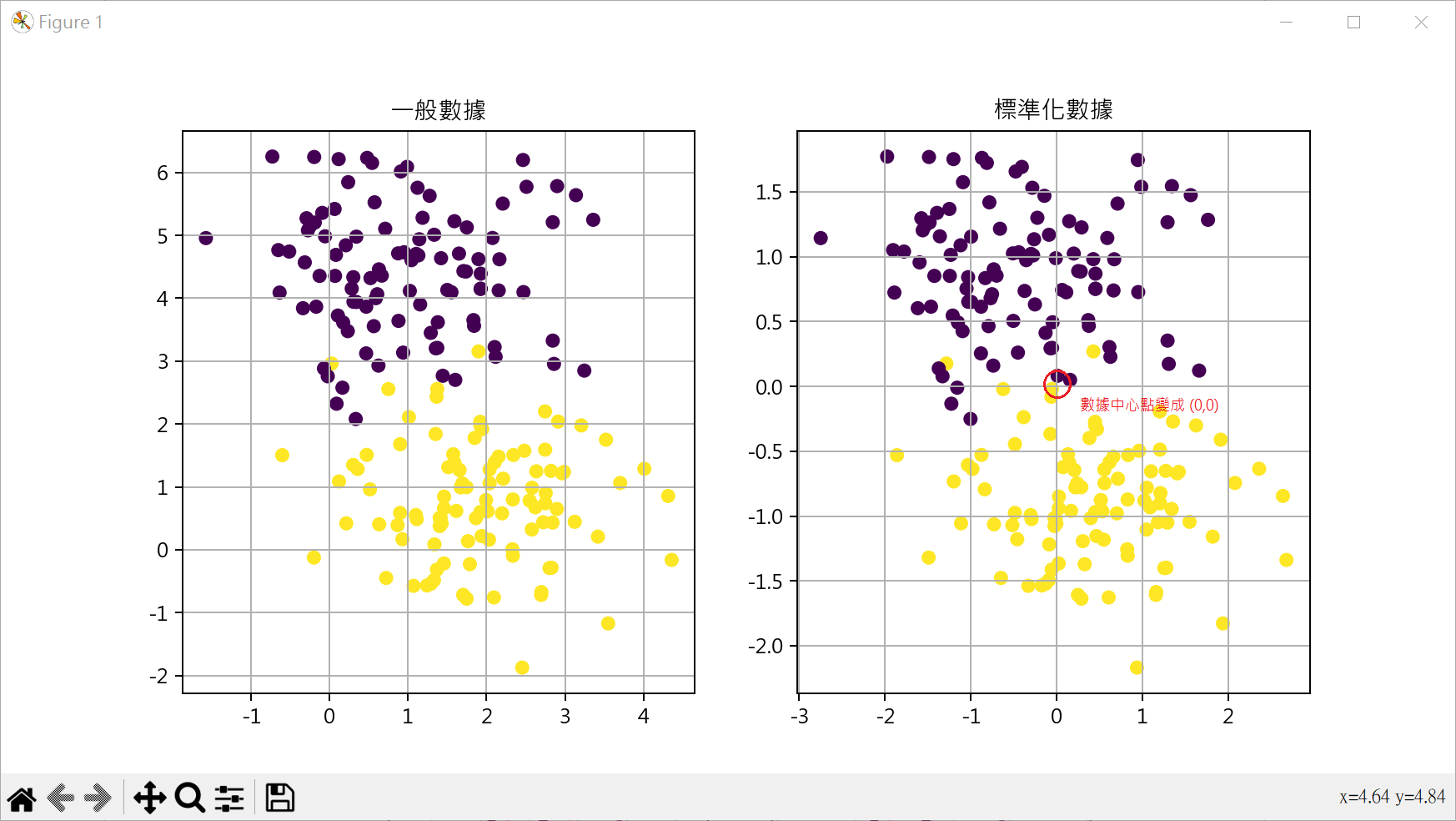
標準化數據 StandardScaler

有時使用 make_blobs()產生的數據,特徵資料的差異會很大,可使用StandardScaler()將資料標準化為平均數是0,變異數是1

1
2
3
from sklearn.preprocessing import StandardScaler
  ...
StandardScaler().fit_transform(data)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 數據中心點變成 (0,0)
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

# windows 使用 微軟正黑體
plt.rcParams["font.family"] = ["Microsoft JhengHei"]
# 顯示負號
plt.rcParams["axes.unicode_minus"] = False

X, y = make_blobs(n_samples=200, n_features=2, centers=2, random_state=0)

X_sta = StandardScaler().fit_transform(X)

# 建立兩個子圖畫布
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10,5))

axs[0].scatter(X[:,0], X[:,1], c=y)
axs[0].set_title("一般數據")
axs[0].grid()

axs[1].scatter(X_sta[:,0], X_sta[:,1], c=y)
axs[1].set_title("標準化數據")
axs[1].grid()

plt.show()
設定數據區間 MinMaxScaler

MinMaxScaler() 主要將資料縮放的最小值和最大值之間,通常是0到1,也可以是其他任意範圍

1
2
3
from sklearn.preprocessing import MinMaxScaler
  ...
MinMaxScaler().fit_transform(data)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 縮放0和1之間數據
from sklearn.datasets import make_blobs
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt

# windows 使用 微軟正黑體
plt.rcParams["font.family"] = ["Microsoft JhengHei"]
# 顯示負號
plt.rcParams["axes.unicode_minus"] = False

X, y = make_blobs(n_samples=200, n_features=2, centers=2, random_state=0)

X_sta = MinMaxScaler().fit_transform(X)

# 建立兩個子圖畫布
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10,5))

axs[0].scatter(X[:,0], X[:,1], c=y)
axs[0].set_title("一般數據")
axs[0].grid()

axs[1].scatter(X_sta[:,0], X_sta[:,1], c=y)
axs[1].set_title("縮放0和1之間數據")
axs[1].grid()

plt.show()
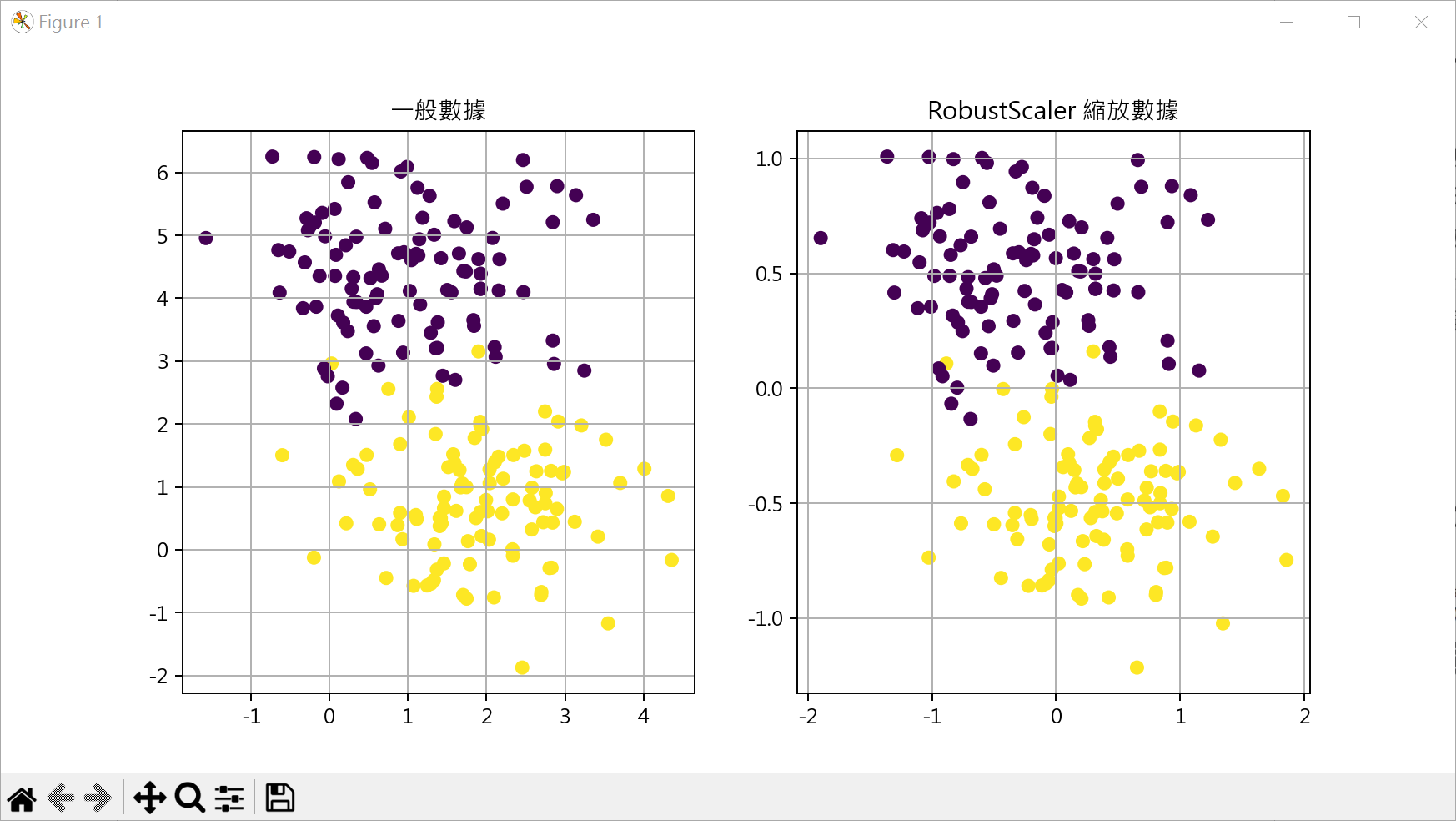
特殊數據縮放 RobusterScaler

RobusterScaler()是一種特殊數據縮放器,特別適合處理含有異常的數據
對於包含異常值的數據,一般縮放方法,可能會受到異常值的影響
RobusterScaler()工作原理是數值減去中位數摒除以四分位距(IQR)IQR是第3四分位距(75%)和第1四分位距(20%)之間的差

1
2
3
from sklearn.preprocessing import MinMaRobusterScalerxScaler
  ...
RobusterScaler().fit_transform(data)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# RobustScaler 縮放數據
from sklearn.datasets import make_blobs
from sklearn.preprocessing import RobustScaler
import matplotlib.pyplot as plt

# windows 使用 微軟正黑體
plt.rcParams["font.family"] = ["Microsoft JhengHei"]
# 顯示負號
plt.rcParams["axes.unicode_minus"] = False

X, y = make_blobs(n_samples=200, n_features=2, centers=2, random_state=0)

X_sta = RobustScaler().fit_transform(X)

# 建立兩個子圖畫布
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(10,5))

axs[0].scatter(X[:,0], X[:,1], c=y)
axs[0].set_title("一般數據")
axs[0].grid()

axs[1].scatter(X_sta[:,0], X_sta[:,1], c=y)
axs[1].set_title("RobustScaler 縮放數據")
axs[1].grid()

plt.show()

機器學習 scikit-learn 入門

使用 scikit-learn LinearRegression 建立線性回歸模型
1
2
3
4
5
6
from sklearn.linear_model import LinearRegression

# 建立線性回歸模型
model = LinearRegression()
# 數據擬合模型 model.fit(X=height, y=weight) 做數據擬合, X必需為二維陣列
model.fit(X, y)
  • model.predict(height) : 預測新數據
  • model.score(X_test, Y_test) : 獲得(X_test, Y_test)數據的R平方值
  • model.intercept_ : 模型方程式的截距
  • model.coef_ : 模型方程式的迴歸係數
  • X 必需為二維陣列,可使用 reshape(-1,1) 將一維轉為二維陣列
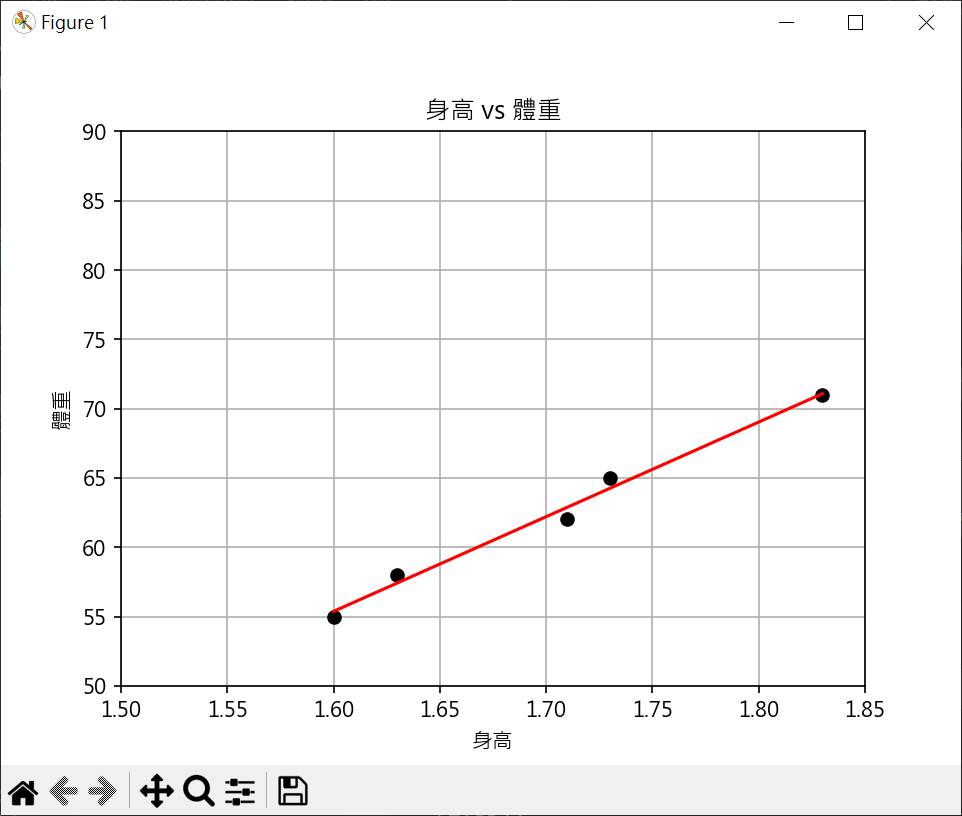
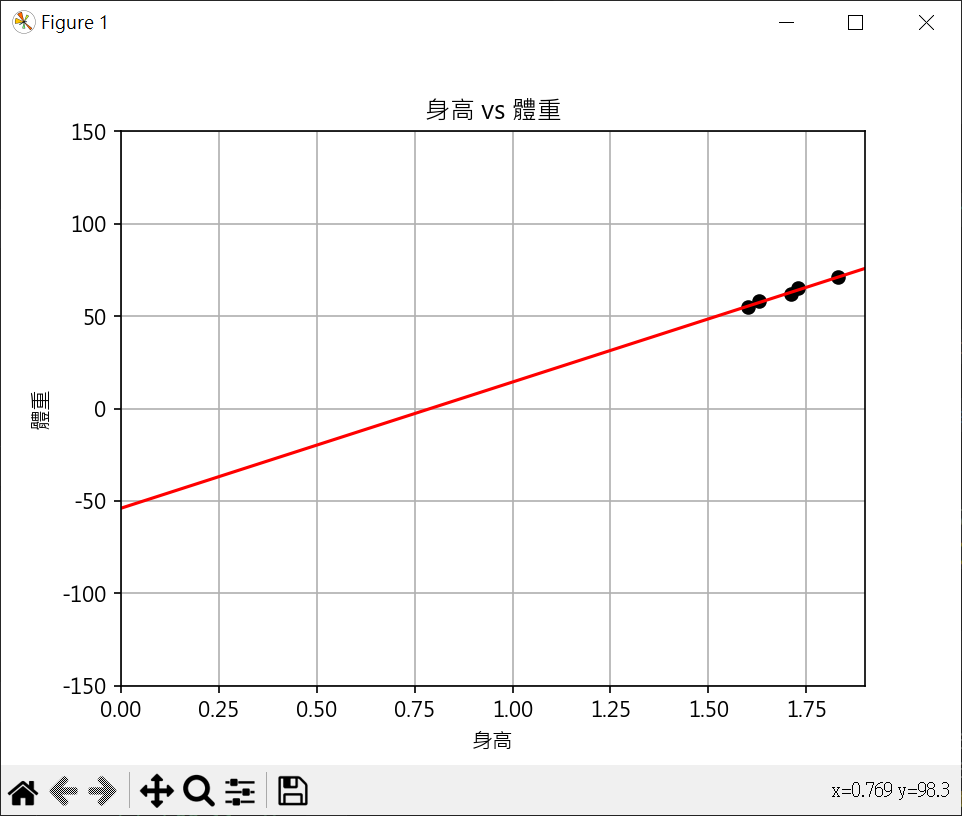
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# 使用 scikit-learn LinearRegression 建立線性回歸模型
# 繪製身高與體重資料圖表
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
import numpy as np

# windows 使用 微軟正黑體
plt.rcParams["font.family"] = ["Microsoft JhengHei"]

# reshape(-1,1) 將一維陣列轉為二維陣列
height = np.array([1.6, 1.63, 1.71, 1.73, 1.83]).reshape(-1,1)
weight = np.array([55, 58, 62, 65, 71])

plt.plot(height, weight, "ko")
plt.axis([1.5, 1.85, 50, 90])
plt.title("身高 vs 體重")
plt.xlabel("身高")
plt.ylabel("體重")

print(f"height={height}")

print(f"height[:,0]={height[:,0]}")
# 建立線性迴歸模型係數
coef = np.polyfit(height[:,0], weight, 1)
# 建立線性迴線函數
reg = np.poly1d(coef)
print(f"reg(height[:,0]) = {reg(height[:,0])}")

# 建立線性回歸模型
model = LinearRegression()
# 數據擬合模型 model.fit(X=height, y=weight) 做數據擬合, X必需為二維陣列
model.fit(X=height, y=weight)
# y_pred = model.predict(X),執行數據預測 X必需為二維陣列
y_pred = model.predict(height)
plt.plot(height, y_pred, c='r')
print(f"y_pred={y_pred}")

# np.polyfit() 與 LinearRegression() 結果是一樣
# height=[[1.6 ]
#  [1.63]
#  [1.71]
#  [1.73]
#  [1.83]]
# height[:,0]=[1.6  1.63 1.71 1.73 1.83]
# reg(height[:,0]) = [55.37073171 57.4195122  62.88292683 64.24878049 71.07804878]
# y_pred=[55.37073171 57.4195122  62.88292683 64.24878049 71.07804878]

plt.grid()
plt.show()
資料預測
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 資料預測
from sklearn.linear_model import LinearRegression
import numpy as np

# reshape(-1,1) 將一維陣列轉為二維陣列
height = np.array([1.6, 1.63, 1.71, 1.73, 1.83]).reshape(-1,1)
weight = np.array([55, 58, 62, 65, 71])

# 建立線性回歸模型
model = LinearRegression()
# model.fit(X=height, y=weight) 做數據擬合, X必需為二維陣列
model.fit(X=height, y=weight)
# y_pred = model.predict(X),執行數據預測 X必需為二維陣列
# y_pred = model.predict(height)
h = int(input("輸入身高(cm):"))
h /= 100
weight_pred = model.predict([[h]])
print(weight_pred)
print(f"預測體重: {weight_pred[0]:.2f} 公斤")
# 輸入身高(cm):175
# [65.61463415]
# 預測體重: 65.61 公斤
模型的儲存與載入
pickle
1
2
3
4
import pickle

pickle.dump(model, save_file)		# save file
model = pickle.load(load_file)	# load file
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 模型儲存 - python's pickle
import pickle
from sklearn.linear_model import LinearRegression
import numpy as np

# reshape(-1,1) 將一維陣列轉為二維陣列
height = np.array([1.6, 1.63, 1.71, 1.73, 1.83]).reshape(-1,1)
weight = np.array([55, 58, 62, 65, 71])

# 建立線性回歸模型
model = LinearRegression()
# model.fit(X=height, y=weight) 做數據擬合, X必需為二維陣列
model.fit(X=height, y=weight)

# 模型儲存
with open("model_ch22_9.pkl", "wb") as f:
    pickle.dump(model, f)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 載入模型 - python's pickle
import pickle

# 載入模型
with open('model_ch22_9.pkl', "rb") as f:
    model = pickle.load(f)

h = int(input("輸入身高(cm):"))
h /= 100
weight_pred = model.predict([[h]])
print(weight_pred)
print(f"預測體重: {weight_pred[0]:.2f} 公斤")
# 輸入身高(cm):175
# [65.61463415]
# 預測體重: 65.61 公斤
joblib (scikit-learn 建議,可有較好的效率)
1
2
3
4
5
from joblib import dump
from joblib import load

dump(model, "model_name.joblib")		# save file
model = load("model_name.joblib")		# load file
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 模型儲存 - joblib(scikit-learn建議)
from joblib import dump
from sklearn.linear_model import LinearRegression
import numpy as np

# reshape(-1,1) 將一維陣列轉為二維陣列
height = np.array([1.6, 1.63, 1.71, 1.73, 1.83]).reshape(-1,1)
weight = np.array([55, 58, 62, 65, 71])

# 建立線性回歸模型
model = LinearRegression()
# model.fit(X=height, y=weight) 做數據擬合, X必需為二維陣列
model.fit(X=height, y=weight)

# 模型儲存
dump(model, "model_ch22_11.joblib")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 載入模型 - joblib(scikit-learn建議)
from joblib import load

# 載入模型
model = load("model_ch22_11.joblib")

h = int(input("輸入身高(cm):"))
h /= 100
weight_pred = model.predict([[h]])
print(weight_pred)
print(f"預測體重: {weight_pred[0]:.2f} 公斤")
# 輸入身高(cm):175
# [65.61463415]
# 預測體重: 65.61 公斤
計算線性迴歸線的斜率和截距
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
# 使用 scikit-learn LinearRegression 建立線性回歸模型
# 繪製身高與體中資料圖表
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
import numpy as np

# windows 使用 微軟正黑體
plt.rcParams["font.family"] = ["Microsoft JhengHei"]
# 顯示負號
plt.rcParams["axes.unicode_minus"] = False

# reshape(-1,1) 將一維陣列轉為二維陣列
height = np.array([1.6, 1.63, 1.71, 1.73, 1.83]).reshape(-1,1)
weight = np.array([55, 58, 62, 65, 71])

plt.plot(height, weight, "ko")
plt.axis([0, 1.9, -150, 150])
plt.title("身高 vs 體重")
plt.xlabel("身高")
plt.ylabel("體重")

# 建立線性回歸模型
model = LinearRegression()
# model.fit(X=height, y=weight) 做數據擬合, X必需為二維陣列
model.fit(X=height, y=weight)

x_line = np.array([0, 1.9]).reshape(-1,1)
# y_pred = model.predict(X),執行數據預測 X必需為二維陣列
y_pred = model.predict(x_line)
plt.plot(x_line, y_pred, c='r')

# 截距與斜率
print(f"y截距 : {model.intercept_:.2f}")
print(f"斜率  : {model.coef_[0]:.2f}")

plt.grid()
plt.show()

# y截距 : -53.90
# 斜率  : 68.29
# 所以方程式為 : weight = 68.29*height - 53.9
R平方係數判定檢驗模型的性能

$ R^2(y,\hat{y}) = 1 - \frac{\sum_{i=1}^{n}(y_i - \hat{y}_i)^2} { \sum _{i=1}^{n}(y_i - \overline{y})^2 } = 1 - \frac{RSS}{TSS}$

  • RSS : Residual Sum of Squares,又稱為殘差平方和(或誤差平方和),表示模型無法解釋的變異性,RSS應盡可能小
  • TSS : Total of Squares,又稱為總平方和,衡量目標變數的變異性,表示目標變數的總變異性,TSS是模型預測值和實際值差異的上限
  • R 平方係數應盡可能接近 1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
from sklearn.linear_model import LinearRegression
import numpy as np
from sklearn.metrics import r2_score

# reshape(-1,1) 將一維陣列轉為二維陣列
height = np.array([1.6, 1.63, 1.71, 1.73, 1.83]).reshape(-1,1)
weight = np.array([55, 58, 62, 65, 71])

# 建立線性回歸模型
model = LinearRegression()
# model.fit(X=height, y=weight) 做數據擬合, X必需為二維陣列
model.fit(X=height, y=weight)

# 手工計算 RSS
# np.ravel 將原陣列降為一維,若修改會影響原值
# np.flatten 將原陣列降為一維,若修改不會影響原值
RSS = np.sum((weight - np.ravel(model.predict(height))) ** 2)
print(f"RSS : {RSS:.2f}")

# 手工計算 TSS
mean_weight = np.mean(weight)
TSS = np.sum((weight - mean_weight) ** 2)
print(f"TSS : {TSS:.2f}")

# 手工計算 R平方係數
R_quare = 1 - (RSS/TSS)
print(f"手工計算 R平方係數 : {R_quare:.2f}")

# 函數計算 R平方係數
# LinearRegression 內含 R平方係數函數,不可使用 sklearn.metrics - r2_score
R_score = model.score(height, weight)
print(f"函數計算 R平方係數 : {R_score:.2f}")
# RSS : 1.82
# TSS : 154.80
# 手工計算 R平方係數 : 0.99
# 函數計算 R平方係數 : 0.99

分類演算法 - 機器學習模型的性能評估

計算精確度 accuracy_score()

計算分類器的準確度

1
2
3
from sklearn.metrics import accuracy_score
	...
accuracy_score(y_true, y_pred, normalize=True, sample_weight=None)
  • y_true : 真實目標值陣列
  • y_pred : 模型預測值
  • normalize : True(default)返回正確比例, Flase返回正確分類總數
  • sample_weight : option,可提供各個權重
1
2
3
4
5
6
7
8
# 精確度
from sklearn.metrics import accuracy_score

y_true = [1, 1, 2, 2, 3, 3]
y_pred = [1, 1, 2, 2, 3, 2]

print(f"Accuacy Score : {accuracy_score(y_true, y_pred)}")
# Accuacy Score : 0.8333333333333334
召回率 recall_score()

計算正標籤正確比例

1
2
3
from sklearn.metrics import recall_score
 ...
recall_score(y_true, y_pred, sample_weight=None)
  • y_true : 真實目標值陣列
  • y_pred : 模型預測值
  • sample_weight : option,可提供各個權重
1
2
3
4
5
6
7
8
# 召回率:計算正類別標籤正確比例
from sklearn.metrics import recall_score

y_true = [1, 1, 0, 0, 1, 1]
y_pred = [1, 0, 0, 0, 1, 1]
print(f"Recall Score : {recall_score(y_true, y_pred)}")
# 正類別標籤(1)有4個,正確預測3個
# Recall Score : 0.75
F1 分數 f1_score()

F1 分數是精確率（Precision）和召回率（Recall）的調和平均數,對於不平衡的數據集,F1分數是一個較好的指標
不平衡數據集（Imbalanced Dataset）指的是在數據集中，不同類別的樣本數量分布不均勻

1
2
3
from sklearn.metrics import f1_score
	...
f1_score(t_true, t_pred, sample_weight=None)

公式如下 :
$F1= 2 × \frac{Precision×Recall
}{Precision+Recall} $
精確率（Precision） 是指在模型預測為正類的所有樣本中，實際為正類的比例。
召回率（Recall） 是指在實際為正類的所有樣本中，被模型正確預測為正類的比例。

計算步驟 :

  • 真正類（True Positives，TP）：正確預測為正類的數量。
  • 偽正類（False Positives，FP）：錯誤預測為正類的數量。
  • 偽負類（False Negatives，FN）：錯誤預測為負類的數量。
  • 真負類（True Negatives，TN）：正確預測為負類的數量。

精確率（Precision） = TP / (TP + FP)
召回率（Recall） = TP / (TP + FN)
Precision = TP / (TP + FP) = 3/(3 + 0) = 1
Recall = TP / (TP + FN) = 3/(3 + 1) = 0.75
F1 = 2 * (PrecisionRecall)/(Precision+Recall) = 2 * (10.75)/(1+0.75) = 0.8571428571

1
2
3
4
5
6
7
# F1 分數:精確率(precision)和召回率(recall)的平均數
from sklearn.metrics import f1_score

t_true = [1, 1, 0, 0, 1, 1]
t_pred = [1, 0, 0, 0, 1, 1]
print(f"F1 Score : {f1_score(t_true, t_pred)}")
# F1 Score : 0.8571428571428571
分類報告 classification_report()

分類報告提供多個類別的性能指標

  • 精確度(Precision):
  • 召回率(Recall):
  • F1分數(F1 Score)
  • 準確度(Accuracy)
  • 算術平均(Macro average):對每個類別進行算術平均
  • 加權平均(Weighted average):對每個類別進行加權平均
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from sklearn.metrics import classification_report

y_true = [1, 1, 0, 1, 0, 0, 1]
y_pred = [1, 0, 1, 1, 1, 0, 1]
report = classification_report(y_true, y_pred)
print("分類報告 :")
print(report)
# 分類報告 :
#               precision    recall  f1-score   support
#            0       0.50      0.33      0.40         3 0 的 F1 Score
#            1       0.60      0.75      0.67         4 1 的 F1 Score
#     accuracy                           0.57         7 準確度
#    macro avg       0.55      0.54      0.53         7 算術平均
# weighted avg       0.56      0.57      0.55         7 加權平均
#										 0.55 = (0.50 + 0.56)/2
#										 0.56 = (0.50 * 3 + 0.60 * 4)/7
混淆矩陣 confusion_maxtrix()

列(row)表實際類別,行(column)表預測類別

1
2
from sklearn.metrics import confusion_matrix
confusion_matrix(y_true, y_pred, sample_weight=None)
1
2
3
4
5
6
7
8
9
10
from sklearn.metrics import confusion_matrix

y_true = [1, 1, 0, 1, 0, 0, 1]
y_pred = [1, 0, 1, 1, 1, 0, 1]
cm = confusion_matrix(y_true, y_pred)
print("混淆矩陣 :")
print(cm)
# 混淆矩陣 :			猜0		 猜1
# [[1 2]			0		1			2
#  [1 3]]			1		1			3
ROC_AUC 分數

roc_auc_score() 用於衡量二元分類器性能的函數
ROC(Receiver Operating Characteristic)接收操作者特性
AUC(Area Under the Curve)ROC曲線下面的面積
roc_auc_score()計算接收者操作特性曲線下面的面積分數的方法

1
2
3
from sklearn.metrics import roc_auc_score
	...
roc_auc_score(y_true, y_scores)
  • y_true : 真實標籤,通常以0和1的形式出現,某些情況下可能是-1和1
  • y_pred : 分類器預測為正類(1)的機率
  • 返回0和1間的分數,越接近1,模型性能越好.越接近0,模型性能越差.若為0.5,相當於隨機猜測.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import matplotlib.pyplot as plt
from sklearn.metrics import roc_auc_score, roc_curve

y_true = [0, 0, 1, 1]
y_scores = [0.1, 0.4, 0.35, 0.8]
auc_score = roc_auc_score(y_true, y_scores)
print(f"ROC AUC 分數 : {auc_score}")
# ROC AUC 分數 : 0.75

# 計算FPR和TPR
fpr, tpr, thresholds = roc_curve(y_true, y_scores)
print(f"fpr={fpr}")
print(f"tpr={tpr}")
print(f"thresholds={thresholds}")
# fpr=[0.  0.  0.5 0.5 1. ]
# tpr=[0.  0.5 0.5 1.  1. ]
# thresholds=[ inf 0.8  0.4  0.35 0.1 ]

# 繪製ROC曲線
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label=f'ROC curve (area = {auc_score:.2f})')
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')

# 標示出梯形的面積區域
for i in range(1, len(fpr)):
    plt.fill_betweenx([0, tpr[i]], fpr[i-1], fpr[i], color='orange', alpha=0.3)

plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic (ROC)')
plt.legend(loc='lower right')
plt.show()

面積計算 = 0.5 * 0.5 + 0.5 * 1 = 0.75

機器學習必須學會的非數值資料轉換

One-hot 編碼

One-hot編碼是一種將類別行變數轉為數執行變數的方法.
pandas get_dummies() 可將類別變數轉為 one-hot 編碼
pd.get_dummies(df, columns=None, prefix=None ,prefix_sep=’_’, drop_first=False)

  • df : 要進行編碼的 DataFrame
  • columns : 要進行編碼的欄位名稱,None 表對所有欄位
  • prefix : 對虛擬變數添加的前綴(default None)
  • prefix_sep : 連接原始欄位名稱和類別名稱的分隔符
  • drop_first : 是否刪除第一個類別的虛擬變數
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import pandas as pd

data = {"color": ["red", "blue", "green", "blue"] }
df = pd.DataFrame(data)
print(df)
#    color
# 0    red
# 1   blue
# 2  green
# 3   blue

# 使用 pandas's get_dummies() 進行 one-hot 編碼
encoded_df = pd.get_dummies(df, columns=['color'])
print(encoded_df)
#    color_blue  color_green  color_red
# 0       False        False       True
# 1        True        False      False
# 2       False         True      False
# 3        True        False      False
特徵名稱由中文改為英文

pd.rename 用於重命名 DataFrame 或 Series 中的標籤（column或index）
pd.rename(mapper=None, index=None, columns=None,
axis=None, inplace=False)

  • mapper : 字典或函數，用於指定新舊標籤之間的映射關係
  • index : 與 mapper 類似，用於指定索引重命名的映射
  • columns : 與 mapper 類似，用於指定列重命名的映射
  • axis : 指定沿哪個軸進行重命名，0 或 ‘index’ 表示重命名索引，1 或 ‘columns’ 表示重命名列。
  • inplace : 默認為 False。如果設置為 True，則會在原 DataFrame 上進行修改，而不返回新對象
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import pandas as pd

df = pd.read_csv("個人資料.csv")
# column 對齊資料
pd.set_option('display.unicode.ambiguous_as_wide', True)
# 若含有中英文資料可以對齊
pd.set_option('display.unicode.east_asian_width', True)

print(df)
print(df.columns)
columns = {
    "編號":"ID",
    "學歷":"Education"
}

df.rename(columns=columns, inplace=True)
print(df.head())
#    編號         學歷
# 0   101         高中
# 1   102         大學
# 2   103         碩士
# 3   104         博士
# 4   105  high_school
# Index(['編號', '學歷'], dtype='object')
#     ID    Education
# 0  101         高中
# 1  102         大學
# 2  103         碩士
# 3  104         博士
# 4  105  high_school
資料對應 map() 方法

pd.map() 可轉換資料為數值資料,字典key是原始資料,直是替換結果

1
2
edu = {'高中':1, '大學':2, '碩士':3, '博士':4, 'high_school':99  }
df['Education'] = df['Education'].map(edu)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# map number to string

import pandas as pd

iris =  pd.Series([0, 1, 2])
print(f"執行 map() 前\n{iris}")
iris = iris.map({0:'setosa', 1:'versicolor', 2:'virginica'})
print(f"執行 map() 後\n{iris}")

# 執行 map() 前
# 0    0
# 1    1
# 2    2
# dtype: int64
# 執行 map() 後
# 0        setosa
# 1    versicolor
# 2     virginica
# dtype: object
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import pandas as pd

df = pd.read_csv("個人資料.csv")
# column 對齊資料
pd.set_option('display.unicode.ambiguous_as_wide', True)
# 若含有中英文資料可以對齊
pd.set_option('display.unicode.east_asian_width', True)

columns = {
    "編號":"ID",
    "學歷":"Education"
}
df.rename(columns=columns, inplace=True)

edu = {'高中':1, '大學':2, '碩士':3, '博士':4, 'high_school':99  }
df['Education'] = df['Education'].map(edu)

print(df.head())
#     ID  Education
# 0  101          1
# 1  102          2
# 2  103          3
# 3  104          4
# 4  105         99
標籤轉換 LabelEncoder()

LabelEncoder() 可將標籤轉換為0 ~ n_classs-1值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from sklearn.preprocessing import LabelEncoder

fruits = ['apple', 'apple', 'chery', 'apple', 'chery', 'orange']
# 創建 LabelEncoder 物件
label = LabelEncoder()

# fit_transform 轉為數值
fruits_encoded = label.fit_transform(fruits)
print(fruits_encoded)

# inverse_transform 轉回原來文字
print(label.inverse_transform(fruits_encoded))
# [0 0 1 0 1 2]
# ['apple' 'apple' 'chery' 'apple' 'chery' 'orange']
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from sklearn.preprocessing import LabelEncoder
from sklearn.tree import DecisionTreeRegressor
import numpy as np

#定義特徵
features =[['晴','熱','弱'],
           ['晴','熱','強'],
           ['陰','熱','弱'],
           ['雨','涼','弱'],
           ['雨','冷','弱'],
           ['雨','冷','強'],
           ['陰','冷','強']]

# 將特徵轉為數字編碼
features_encoded = []
for i in range(len(features[0])):
    # 創建 LabelEncoder 物件
    le = LabelEncoder()
    # fit_transform 轉為數值
    feature_encoded = le.fit_transform([row[i] for row in features])
    features_encoded.append(feature_encoded)
# 3*7 陣列,轉成 7*3 陣列
features_encoded = np.array(features_encoded).T
print(f"特徵標籤編碼\n{features_encoded}")
# 特徵標籤編碼
# [[0 2 0]
#  [0 2 1]
#  [1 2 0]
#  [2 1 0]
#  [2 0 0]
#  [2 0 1]
#  [1 0 1]]

機器學習演算法

  • 監督學習法
    • 線性迴歸
    • 邏輯迴歸
    • KNN 演算法
    • 支持向量機(SVM)
    • 決策樹
    • 隨機森林
  • 無監督學習法
    • 分群(或稱聚類)分析(如:K-means)
    • 降維(如:主成份分析(PCA))

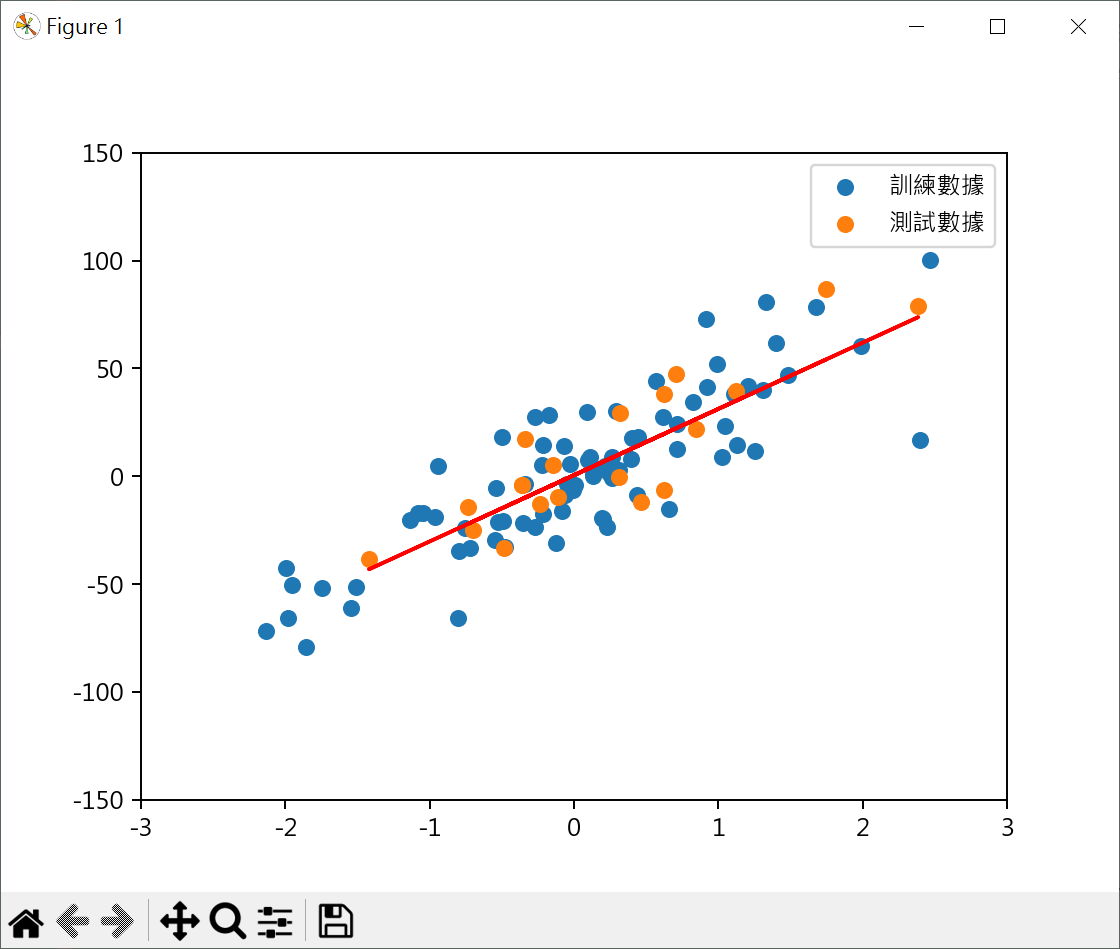
使用隨機數據學習性迴歸

使用隨機數據測試迴歸模型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score
import matplotlib.pyplot as plt

# windows 使用 微軟正黑體
plt.rcParams["font.family"] = ["Microsoft JhengHei"]
# 顯示負號
plt.rcParams["axes.unicode_minus"] = False

# 生成數據
X, y = make_regression(n_features=1, noise=20, random_state=10)

# 分割測試數據與測試數據
X_train, X_test, y_train, y_test = \
    train_test_split(X, y, test_size=0.2, random_state=10)

# 建立線性回歸模型
model = LinearRegression()
# 數據擬合模型 model.fit(X=height, y=weight) 做數據擬合, X必需為二維陣列
model.fit(X=X_train, y=y_train)

# 繪資料圖
plt.scatter(X_train, y_train, label="訓練數據")
plt.scatter(X_test, y_test, label="測試數據")

# 繪迴歸線
y_pred = model.predict(X_test)
plt.plot(X_test, y_pred, color='red')

# 計算 R 平方數
print(f"R2_Score:{r2_score(y_test, y_pred):.2f}")

plt.legend()
plt.axis([-3, 3, -150, 150])
plt.show()
# R2_Score:0.76
score() 和 r2_score() 的差異

scikit-learn 中 score() 和 r2_score() 都可以計算R平方判定係數,但場景有一些差異

  • score(X, y) :

    1
    2
    3
    from sklearn.linear_model import LinearRegression
    model = LinearRegression().fit(X_train, y_train)
    r2 = model.score(x_test, y_test)

  • r2_score(y_true, y_pred) :

    1
    2
    3
    from sklearn.metrics import r2_score
    y_pred = model.predict(X_test)
    r2 = r2_score(y_test, y_pred)

如果你想快速地在個模型上計算R平方判定係數,score(X, y)較方便,如你需要更多的靈活性,如比對不同模型的預測效果,或你已有預測結果,r2_score(y_true, y_pred)可能更適合

其他

儲存公式

# 邏輯迴歸模型語法基礎

數據

創建聚類算法的測試數據集
# 繪製散點圖
生成合成線性回歸數據集
# 線性回歸數據集-繪製散點圖

邏輯迴歸

基本計算
# 邏輯迴歸模型語法基礎
特徵縮放 - 對邏輯迴歸很重要,因各特徵數值大小有差異
# 用最相關2個特徵,設計邏輯迴歸模型

決策樹

基本例子
# 天氣數據實例
繪製決策樹
# 繪製決策樹