matplotlib.pyplot 3D

發表於 更新於 分類於 Disqus：
文章字數： 3k 所需閱讀時間 ≈ 3 分鐘

some special

3D 表面圖 - plot_surface()

1
2
3
4
# 繪製超平面
grid = np.linspace(-1.5, 1.5)
xx, yy = np.meshgrid(grid, grid)
ax.plot_surface(xx, yy, x3(xx, yy), color='gray', alpha=0.5)

Example

二元函數3D圖(Z=X+Y)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# Z = X + Y
import matplotlib.pyplot as plt
import numpy as np

# windows 使用 微軟正黑體
plt.rcParams["font.family"] = ["Microsoft JhengHei"]
# 顯示負號
plt.rcParams["axes.unicode_minus"] = False

# 畫單張圖
# fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
# or
fig = plt.figure()
ax = fig.add_subplot(projection='3d')

# 多單張圖
# fig = plt.figure(figsize= (10, 8))
# ax1 = fig.add_subplot(121, projection='3d')
# ax1 = fig.add_subplot(122, projection='3d')

# 建立資料
x = np.arange(start=-4, stop=5)
y = np.arange(start=-4, stop=5)
X, Y = np.meshgrid(x, y)
# 建立子圖
Z = X + Y

# 繪製 3D 圖
ax.scatter(X, Y, Z, color='b')  # 散佈圖
ax.plot_wireframe(X, Y, Z, color='g') # 繪製 3D 框線

# set title
ax.set_title('繪圖3D網格圖', fontsize=16, color='b')
# set label
ax.set_xlabel('X軸', color='g')
ax.set_ylabel('Y軸', color='g')
ax.set_zlabel('Z軸', color='g')

plt.show()

等高圖

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# 等高圖
# f(x,y) = sin(..)
import matplotlib.pyplot as plt
import numpy as np

# windows 使用 微軟正黑體
plt.rcParams["font.family"] = ["Microsoft JhengHei"]
# 顯示負號
plt.rcParams["axes.unicode_minus"] = False

x = np.linspace(-5, 5, 30)
y = np.linspace(-5, 5, 30)
X, Y = np.meshgrid(x, y)
Z = np.sin(np.sqrt(X**2 + Y**2))

fig = plt.figure(figsize= (10, 6))
ax1 = fig.add_subplot(221, projection='3d')
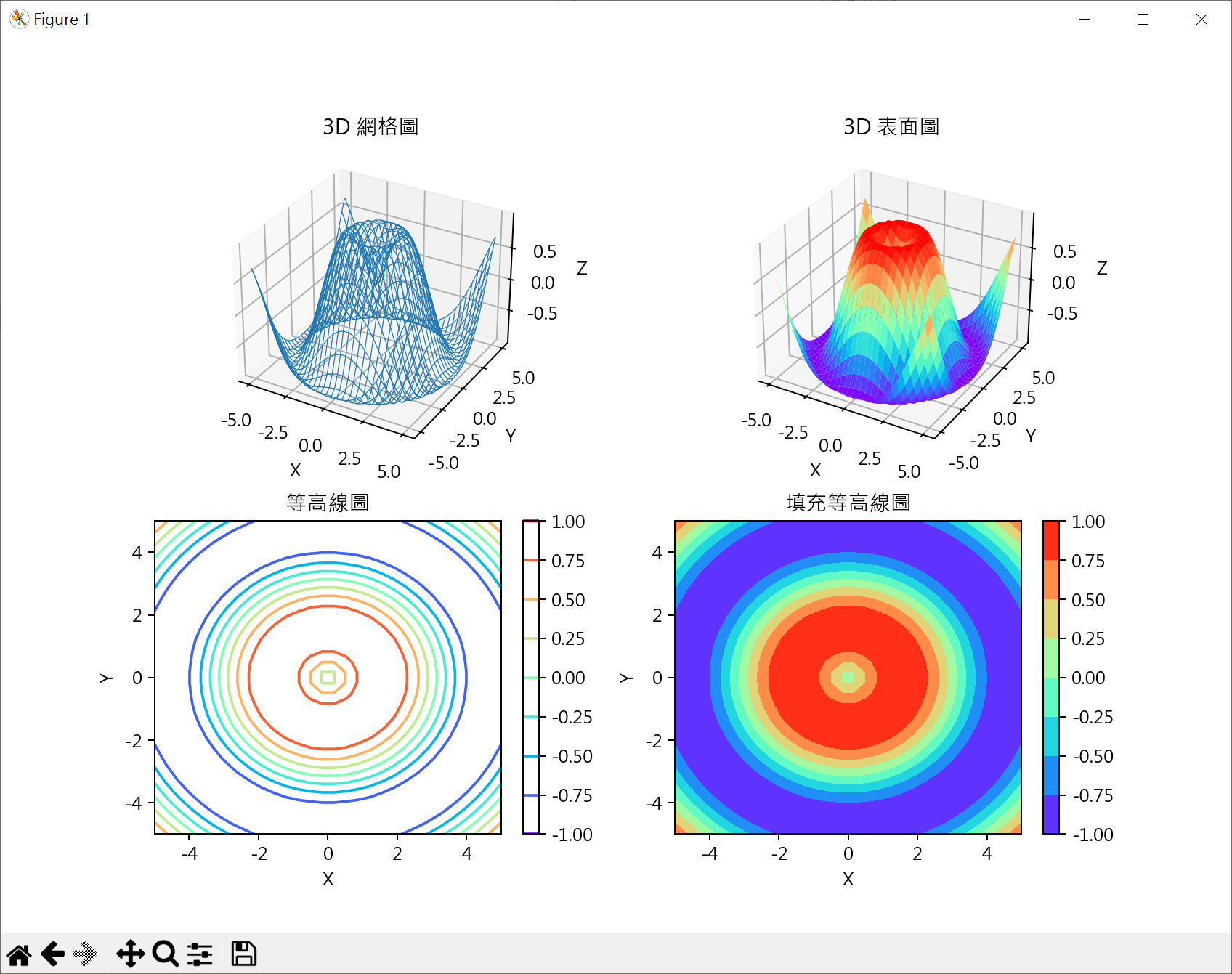
ax1.plot_wireframe(X, Y, Z, linewidth=0.5, cmap="rainbow") # 繪製 3D 框線
ax1.set_title('3D 網格圖')
# set label
ax1.set_xlabel('X')
ax1.set_ylabel('Y')
ax1.set_zlabel('Z')

ax2 = fig.add_subplot(222, projection='3d')
ax2.plot_surface(X, Y, Z, cmap="rainbow")  # 繪製 3D 表面圖
ax2.set_title('3D 表面圖')
# set label
ax2.set_xlabel('X')
ax2.set_ylabel('Y')
ax2.set_zlabel('Z')

ax3 = fig.add_subplot(223)
countour = ax3.contour(X, Y, Z, cmap="rainbow") # 繪製 3D 框線
ax3.set_title('等高線圖')
# set label
ax3.set_xlabel('X')
ax3.set_ylabel('Y')
fig.colorbar(countour)

ax4 = fig.add_subplot(224)
countourf = ax4.contourf(X, Y, Z, cmap="rainbow")  # 繪製 3D 表面圖
ax4.set_title('填充等高線圖')
# set label
ax4.set_xlabel('X')
ax4.set_ylabel('Y')
fig.colorbar(countourf)

plt.show()

創建網格坐標

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# np.meshgrid 用於創建網格坐標
# 在科學計算和數據可視化中非常有用，特別是當你需要在網格上計算函數並繪製3D圖形時
import numpy as np

x = [0, 1, 2, 3, 4 ,5]
y = [6 , 7 , 8, 9]

XX, YY = np.meshgrid(x, y)
print(f"XX\n{XX}")
print(f"YY\n{YY}")

ZZ = XX + 5 * YY
print(f"ZZ\n{ZZ}")

# XX
# [[0 1 2 3 4 5]
#  [0 1 2 3 4 5]
#  [0 1 2 3 4 5]
#  [0 1 2 3 4 5]]
# YY
# [[6 6 6 6 6 6]
#  [7 7 7 7 7 7]
#  [8 8 8 8 8 8]
#  [9 9 9 9 9 9]]
# ZZ
# [[30 31 32 33 34 35]
#  [35 36 37 38 39 40]
#  [40 41 42 43 44 45]
#  [45 46 47 48 49 50]]

Ref