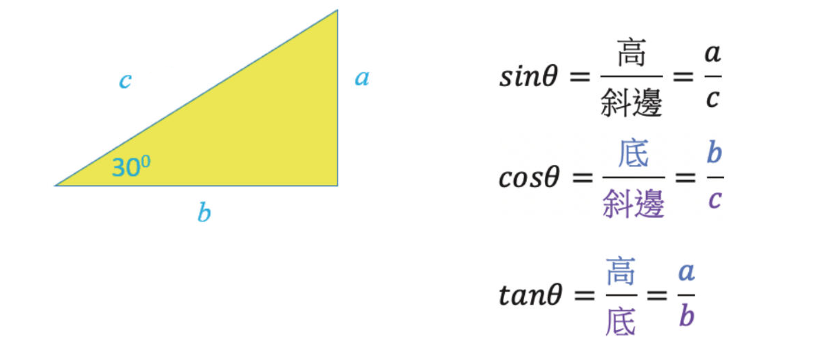名詞 一般名詞
人工智慧(Articial Intelligence)
機器學習(Machine Learning)
深入學習(Deep Learning)
神經網路(Neural Network)
卷積神經網路(Convolutional Neural Network)
Tensorflow
機器學習
監督學習(supervised learning):以已知輸入和輸出數據進行學習,找出輸入及輸出之間的關係,一搬將80%(or 70%)數據用於訓練,20%(or 30%)用於測試
無監督學習(unsupervised learning):沒有目標,主要用於找出數據結構,識別模式和關係
強化學習(reinforcement learning):沒有明確訓練資料與標準答案,機器必須在給予環境中自我學習,然後評估行動回饋是正面或負面,進而調整下次行動,進而獲得正確答案
機器學習應用
圖像辨識
自然語言處理:用於理解,生成和翻譯人類語言.使得可進行情感分析,機器翻譯,語音辨識和自然語言回應
推薦系統:依用戶瀏覽及購買歷史,提供產品及服務的推薦
金融領域:檢測欺詐交易,評估信用風險,預測股票價格波動
醫療領域:分析醫療數據,幫助醫生診斷,預測病情發展
物聯網:優化智慧家居,智慧城市,能源管理,設備維護,安全監控
遊戲領域:使遊戲腳色可根據玩家行為自主決策及適應,遊戲測試,優化,自動發現問題即提出改善方案
廣告投射:分析用戶行為,精準投射廣告
工業自動化:應用於機器人和自動化設備,使能夠在無人工干預下,自動完成生產,檢測和維護
客戶諮詢:開發智慧服務機器人,自動回答用戶問題,處理用戶諮詢,提高客戶效率和滿意度
社交媒體:分析用戶行為,用於客戶分類,內容過濾,情感分析,提供更優質的社交體驗
供應鏈管理:預測供應鏈中的需求,供應和運輸,提供有效的庫存管理,物流規劃和風險管理
深度學習
深度學習主要關注使用人工精神網路來模擬人類大腦過程
深度學習在許多領域取的顯著得成果,如語音辨識,圖像辨識,自然語言處理及遊戲
常見的神經網路類型包含
數學
線性迴歸:依蒐集到的數據,找出與數據最近的一條直線,或稱為最近函數
方程式與函數 二元函數 sympy sympy 說明 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 import sympy as spx = sp.Symbol('x' ) y = sp.Symbol('y' ) print (x.name)print (x + x + 2 )z = 5 *x + 6 *y + x*y print (z)a, b, c = sp.symbols(('a' , 'b' , 'c' )) print (a.name, b.name, c.name)eq2 = sp.sin(x**2 ) + sp.log(8 ,2 )*x + sp.log(sp.exp(3 )) result2 = eq2.subs({x:1 }) print (result2)print (result2.evalf())
解一元一次方程式 1 2 3 4 5 6 7 8 9 10 11 import sympy as spx = sp.Symbol('x' ) eq = 3 *x + 5 - 8 ans = sp.solve(eq) print (ans)print (type (ans))
解聯立方程式 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 from sympy import Symbol, solvea = Symbol("a" ) b = Symbol("b" ) eq1 = a + b - 1 eq2 = 5 *a + b -2 ans = solve((eq1, eq2)) print (type (ans))print (ans)print (f"a={ans[a]} " )print (f"b={ans[b]} " )
解一元二次方程式 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 from sympy import *x = Symbol("x" ) f = x**2 - 2 *x - 8 roots = solve(f) print (roots)f = x**2 - 2 *x + 1 roots = solve(f) print (roots)f = x**2 + x + 1 roots = solve(f) print (roots)number_roots = [root.evalf() for root in roots] print (number_roots)
FiniteSet - 建立集合 1 2 3 4 5 6 7 8 9 10 11 from sympy import FiniteSetA = FiniteSet(1 , 2 , 3 ) print (A)a = A.powerset() print (a)
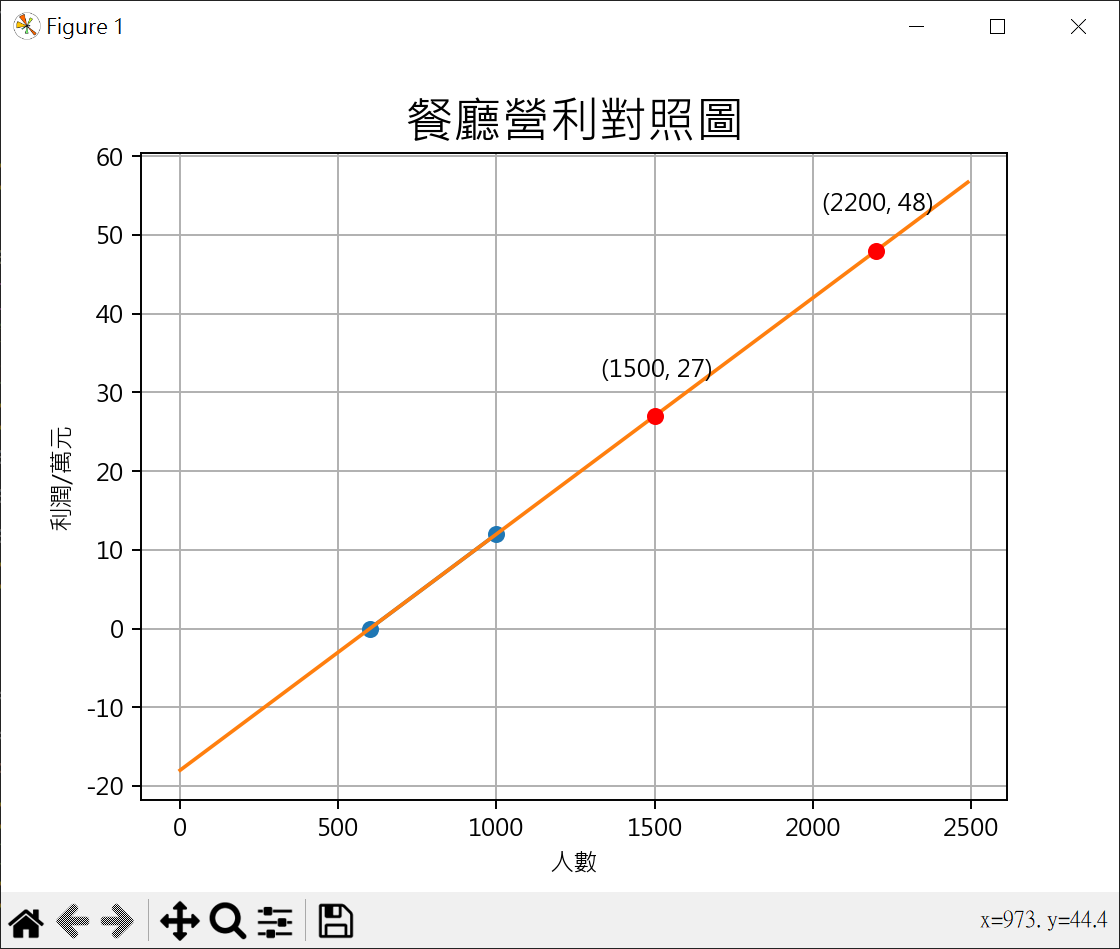
聯立方程式 餐廳營利計算 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 from sympy import Symbol, solvea = Symbol("a" ) b = Symbol("b" ) eq1 = 600 * a + b eq2 = 1000 * a + b - 12 ans = solve((eq1, eq2)) print (f"a={ans[a]} " )print (f"b={ans[b]} " )import matplotlib.pyplot as pltplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False points_x = [600 , 1000 ] points_y = [ px * ans[a] + ans[b] for px in points_x] plt.plot(points_x, points_y, "-o" ) x = range (0 , 2500 , 10 ) y = [ans[a] * y - 18 for y in x] plt.plot(x,y) plt.title('餐廳營利對照圖' , fontsize=20 ) plt.xlabel('人數' ) plt.ylabel('利潤/萬元' ) plt.grid() people1 = 1500 frofit1 = people1 * ans[a] + ans[b] print (f"f({people1} ) = {frofit1} " )plt.plot(people1, frofit1, "-o" , color='red' ) plt.text(people1-170 , frofit1+5 , f"({people1} , {frofit1} )" ) frofit2 = 48 people2 = (frofit2 - ans[b]) / ans[a] print (f"f({people2} ) = {frofit2} " )plt.plot(people2, frofit2, "-o" , color='red' ) plt.text(people2-170 , frofit2+5 , f"({people2} , {frofit2} )" ) plt.show()
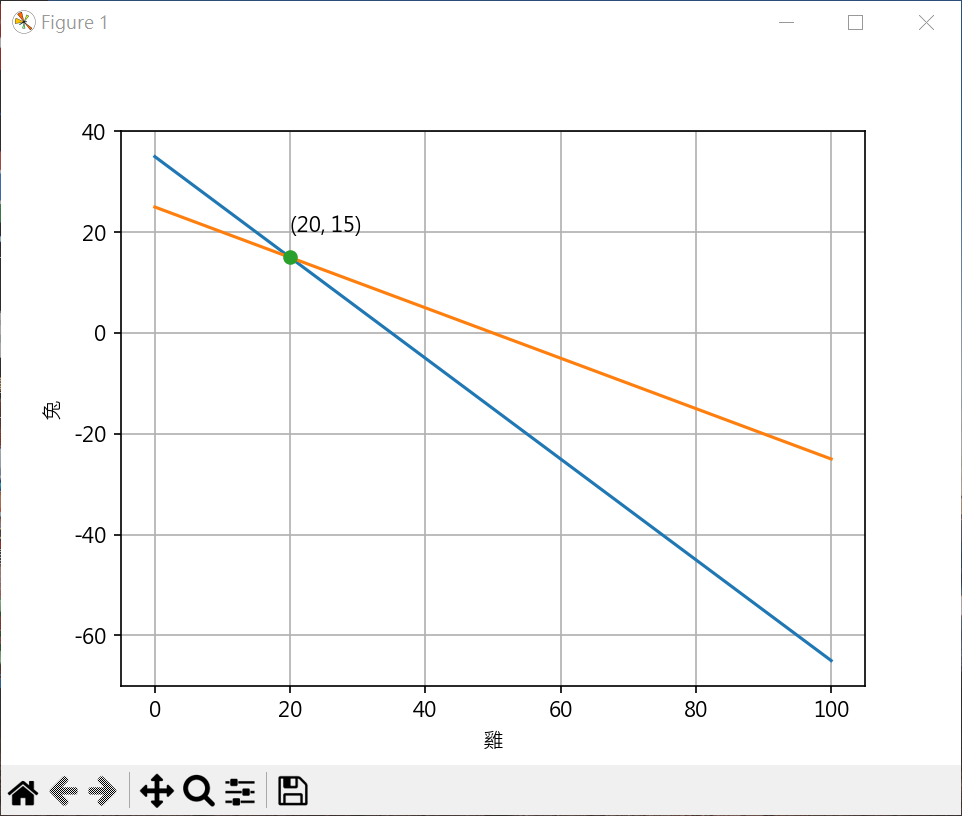
雞兔同籠 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 from sympy import Symbol, solvex = Symbol("x" ) y = Symbol("y" ) eq1 = x + y - 35 eq2 = 2 *x + 4 *y -100 ans = solve((eq1, eq2)) print (ans)print (f"雞={ans[x]} " )print (f"兔={ans[y]} " )import matplotlib.pyplot as pltplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False x_p = range (0 ,101 ) y1_p = [ 35 - x_no for x_no in x_p] y2_p = [ (100 - 2 *x_no)/4 for x_no in x_p] plt.plot(x_p, y1_p) plt.plot(x_p, y2_p) plt.plot(ans[x], ans[y], "-o" ) plt.text(ans[x], ans[y]+5 , f"({ans[x]} , {ans[y]} )" ) plt.xlabel('雞' ) plt.ylabel('兔' ) plt.grid() plt.show()
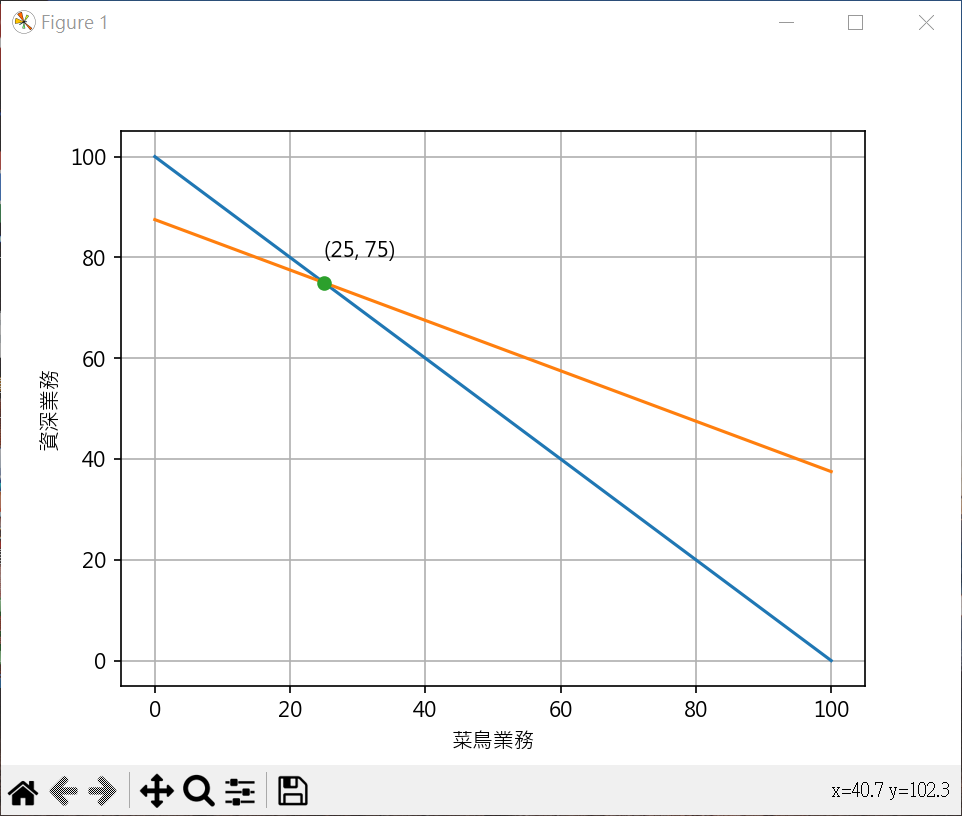
業務目標計算 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 from sympy import Symbol, solvex = Symbol("x" ) y = Symbol("y" ) eq1 = x + y - 100 eq2 = 2 *x + 4 *y - 350 ans = solve((eq1, eq2)) print (ans)print (f"菜鳥業務={ans[x]} " )print (f"資深業務={ans[y]} " )import matplotlib.pyplot as pltplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False line_x = range (0 ,101 ) line1_y = [ 100 - x_no for x_no in line_x] line2_y = [ (350 - 2 *x_no)/4 for x_no in line_x] plt.plot(line_x, line1_y) plt.plot(line_x, line2_y) plt.plot(ans[x], ans[y], "-o" ) plt.text(ans[x], ans[y]+5 , f"({ans[x]} , {ans[y]} )" ) plt.xlabel('菜鳥業務' ) plt.ylabel('資深業務' ) plt.grid() plt.show()
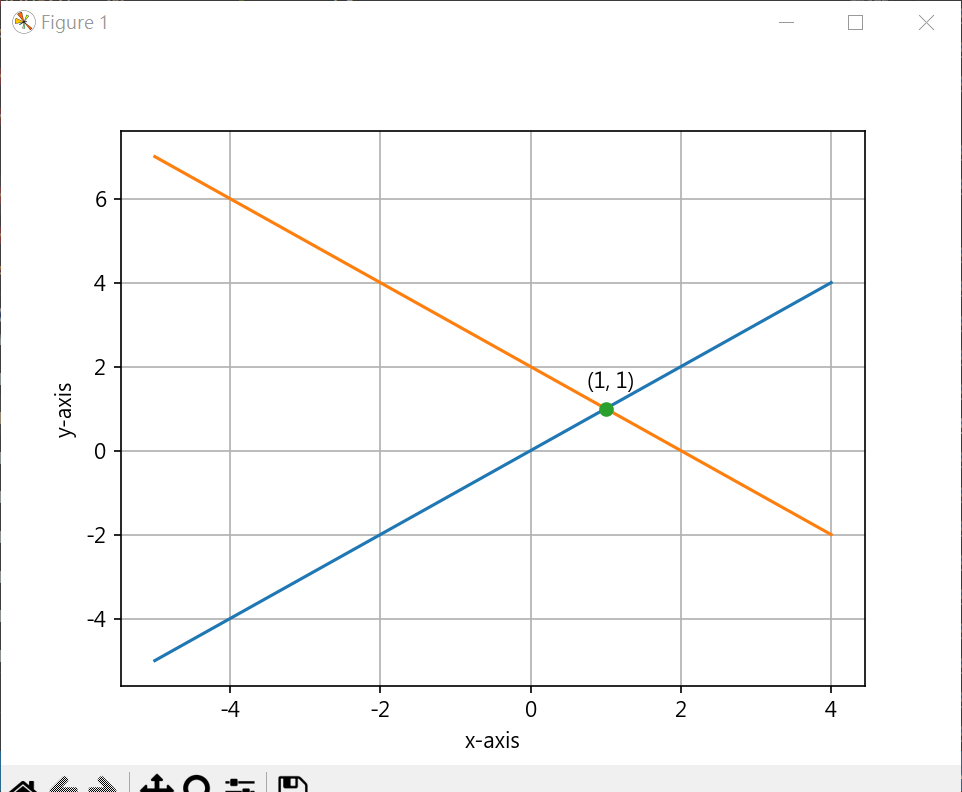
垂直相交線 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 from sympy import Symbol, solvex = Symbol("x" ) y = Symbol("y" ) eq1 = x - y eq2 = -x + 2 - y ans = solve((eq1, eq2)) print (ans)import matplotlib.pyplot as pltplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False line_x = range (-5 ,5 ) line1_y = [ x_no for x_no in line_x] line2_y = [ -x_no + 2 for x_no in line_x] plt.plot(line_x, line1_y) plt.plot(line_x, line2_y) plt.plot(ans[x], ans[y], "-o" ) plt.text(ans[x]-0.25 , ans[y]+0.5 , f"({ans[x]} , {ans[y]} )" ) plt.xlabel('x-axis' ) plt.ylabel('y-axis' ) plt.grid() plt.show()
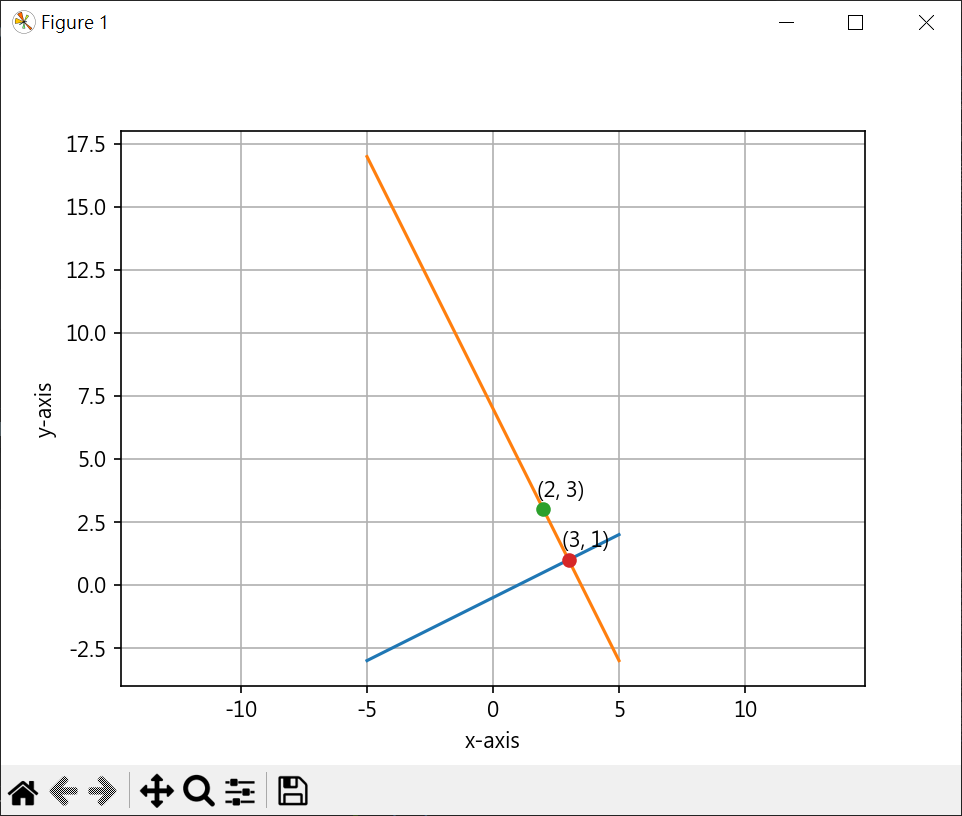
求某一點至一條線垂直線 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 from sympy import Symbol, solvex = Symbol("x" ) y = Symbol("y" ) eq1 = 0.5 *x - 0.5 - y eq2 = -2 *x + 7 - y ans = solve((eq1, eq2)) print (ans)import matplotlib.pyplot as pltplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False line_x = range (-5 ,6 ) line_y = [0.5 *x_no - 0.5 for x_no in line_x] plt.plot(line_x, line_y) line2_x = range (-5 ,6 ) line2_y = [-2 *x_no + 7 for x_no in line2_x ] plt.plot(line2_x, line2_y) point_x = 2 point_y = 3 plt.plot(point_x, point_y, "-o" ) plt.text(point_x-0.25 , point_y+0.5 , f"({point_x} , {point_y} )" ) plt.plot(ans[x], ans[y], "-o" ) plt.text(ans[x]-0.25 , ans[y]+0.5 , f"({int (ans[x])} , {int (ans[y])} )" ) plt.xlabel('x-axis' ) plt.ylabel('y-axis' ) plt.grid() plt.axis('equal' ) plt.show()
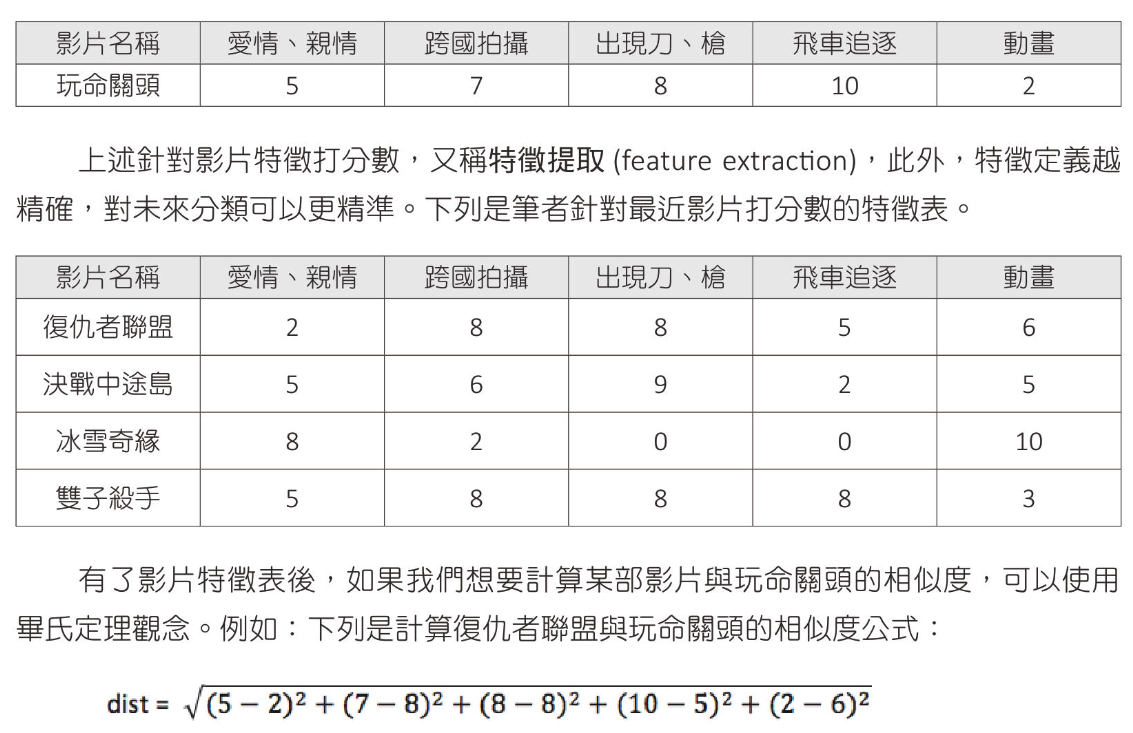
畢氏定理 電影分類
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 import mathfilm = [5 , 7 , 8 , 10 , 2 ] film_titles = [ "復仇者聯盟" , "決戰中途島" , "冰雪奇緣" , "雙子殺手" ] film_features = [ [2 , 8 , 8 , 5 , 6 ], [5 , 6 , 9 , 2 , 5 ], [8 , 2 , 0 , 0 , 10 ], [5 , 8 , 8 , 8 , 3 ] ] dists =[] for p in film_features: distance = 0 for i, item in enumerate (p): score = int (item) - int (film[i]) distance += score * score dists.append(math.sqrt(distance)) good_point = 0 good_distance = dists[0 ] for index, value in enumerate (dists): print (f"{film_titles[index]} : {value:.2 f} " ) if index > 0 and dists[index] < good_distance: good_point = index good_distance = dists[index] print (f"close movie is {film_titles[good_point]} : {dists[good_point]:.2 f} " )
計算兩個向量的歐幾乎里德距離 1 2 3 4 5 6 7 8 import numpy as npa = np.array([1 , 2 , 3 ]) b = np.array([4 , 5 , 6 ]) distance = np.sqrt(np.sum ((a-b)**2 )) print (f"a and b 距離 : {distance:.2 f} " )
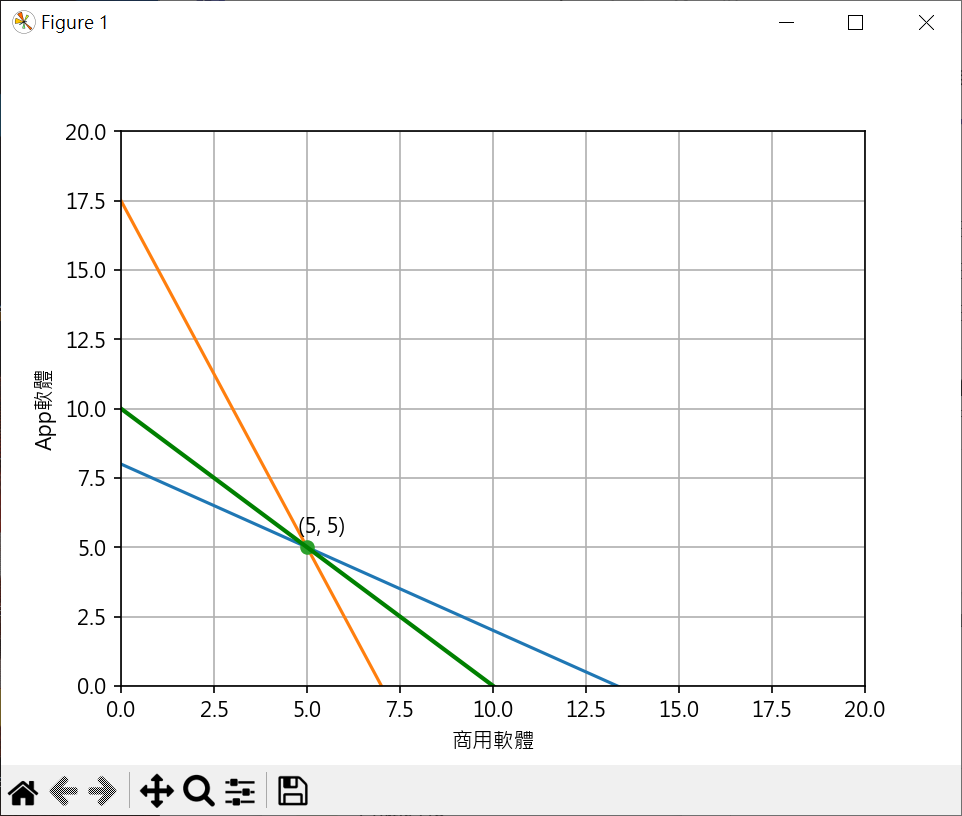
聯立不等式 開發分析 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 from sympy import Symbol, solvex = Symbol("x" ) y = Symbol("y" ) eq1 = -0.6 *x + 8 - y eq2 = -2.5 *x + 17.5 - y ans = solve((eq1, eq2)) print (ans)import matplotlib.pyplot as pltplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False line_x = range (0 ,15 ) line1_y = [ -0.6 *x_no + 8 for x_no in line_x ] line2_y = [ -2.5 *x_no + 17.5 for x_no in line_x ] plt.plot(line_x, line1_y) plt.plot(line_x, line2_y) plt.plot(ans[x], ans[y], "-o" ) plt.text(ans[x]-0.25 , ans[y]+0.5 , f"({int (ans[x])} , {int (ans[y])} )" ) line3_x = range (0 ,15 ) line3_y = [ -x_no + 10 for x_no in line3_x ] plt.plot(line3_x, line3_y, lw='2.0' , color="green" ) plt.xlabel('商用軟體' ) plt.ylabel('App軟體' ) plt.axis([0 , 20 , 0 , 20 ]) plt.grid() plt.show()
二次函數
解一元二次方程式的根 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 from sympy import *x = Symbol("x" ) f = x**2 - 2 *x - 8 roots = solve(f) print (roots)f = x**2 - 2 *x + 1 roots = solve(f) print (roots)f = x**2 + x + 1 roots = solve(f) print (roots)number_roots = [root.evalf() for root in roots] print (number_roots)f = 3 *(x-2 )**2 - 2 roots = solve(f) print (roots)number_roots = [root.evalf() for root in roots] print (number_roots)
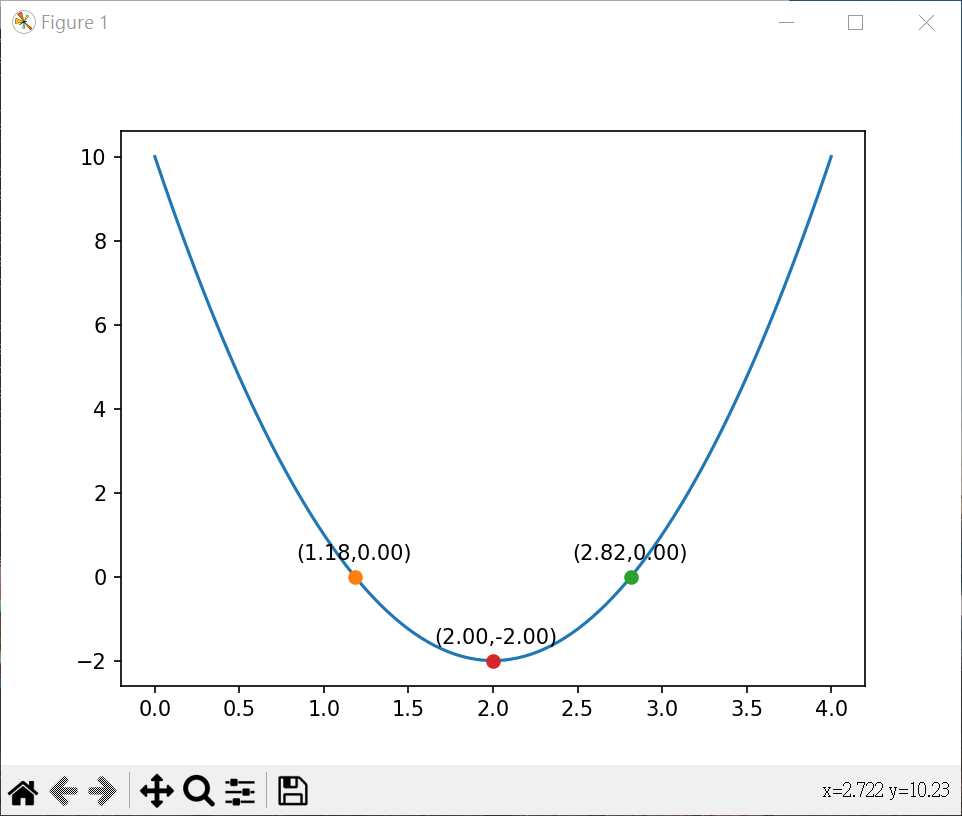
一元二次方程式繪圖並算極值 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 from sympy import *x = Symbol("x" ) f = 3 *x**2 -12 *x + 10 roots = solve(f) def f (x ) : return 3 *x**2 -12 *x + 10 def g (x ) : return -f(x) def f2 (x ) : return -3 *x**2 +12 *x - 9 def g2 (x ) : return -f2(x) import matplotlib.pyplot as pltimport numpy as npfrom scipy.optimize import minimize_scalarline_x = np.linspace(0 , 4 , 100 ) line_y = 3 *line_x**2 - 12 *line_x + 10 plt.plot(line_x, line_y) for root in roots: x_value = root.evalf() y_value = f(x_value) plt.plot(x_value, y_value, "-o" ) plt.text(x_value - 0.35 , y_value + 0.4 , f"({x_value:.2 f} ,{y_value:.2 f} )" ) peak = minimize_scalar(f) if not (np.isinf(peak.fun)): limit_y = peak.fun else : peak = minimize_scalar(g) if not (np.isinf(peak.fun)): limit_y = -peak.fun if not (np.isinf(peak.fun)): plt.plot(peak.x, limit_y, "-o" ) plt.text(peak.x - 0.35 , limit_y + 0.4 , f"({peak.x:.2 f} ,{limit_y:.2 f} )" ) plt.show()
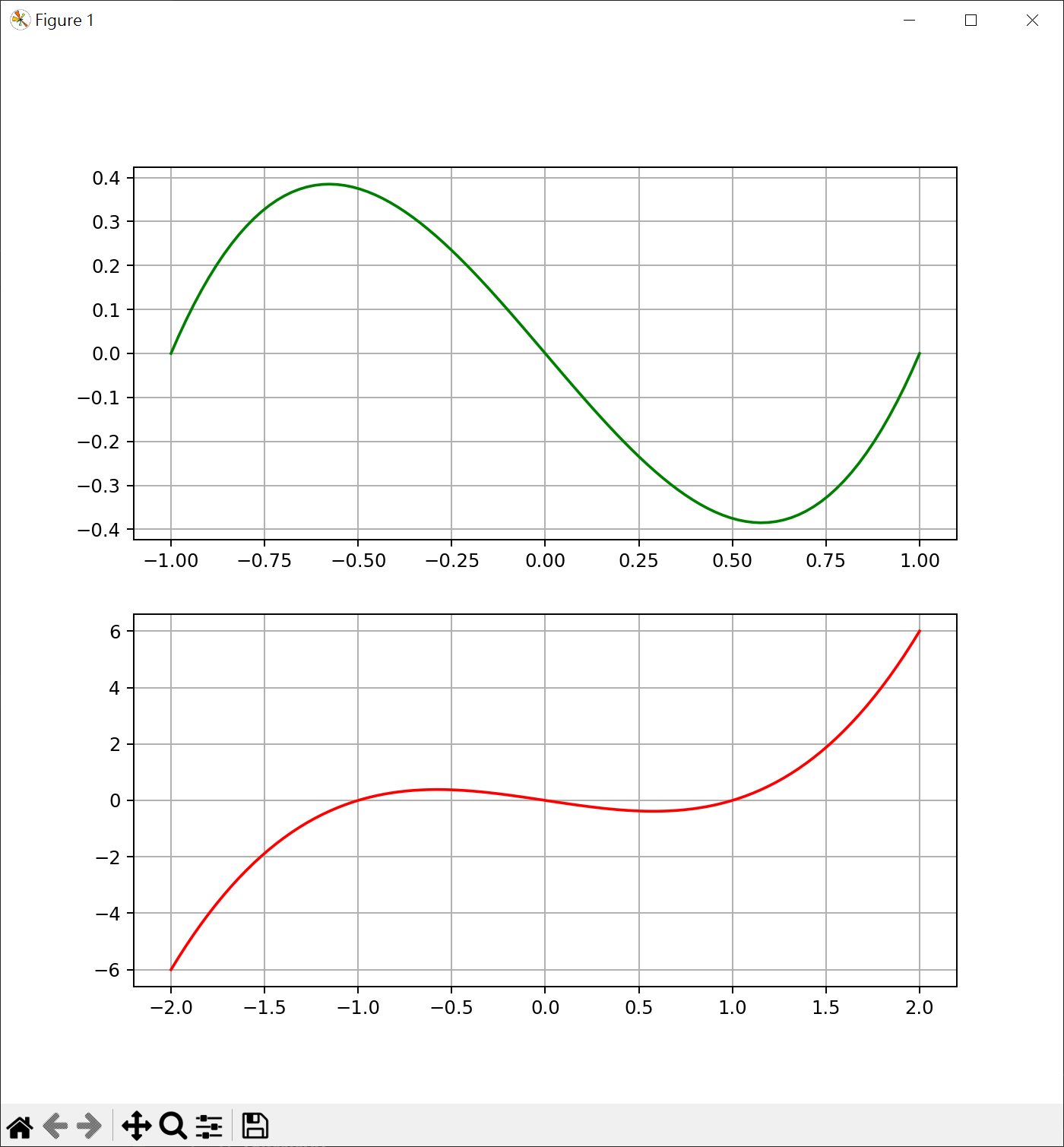
一元三次圖形繪製 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 import matplotlib.pyplot as pltimport numpy as npplt.figure(figsize=[8 ,8 ]) plt.subplot(2 ,1 ,1 ) line_x = np.linspace(-1 , 1 , 100 ) line_y = line_x**3 - line_x plt.plot(line_x, line_y, color="green" ) plt.grid() plt.subplot(2 ,1 ,2 ) line2_x = np.linspace(-2 , 2 , 100 ) line2_y = line2_x**3 - line2_x plt.plot(line2_x, line2_y, color="red" ) plt.grid() plt.show()
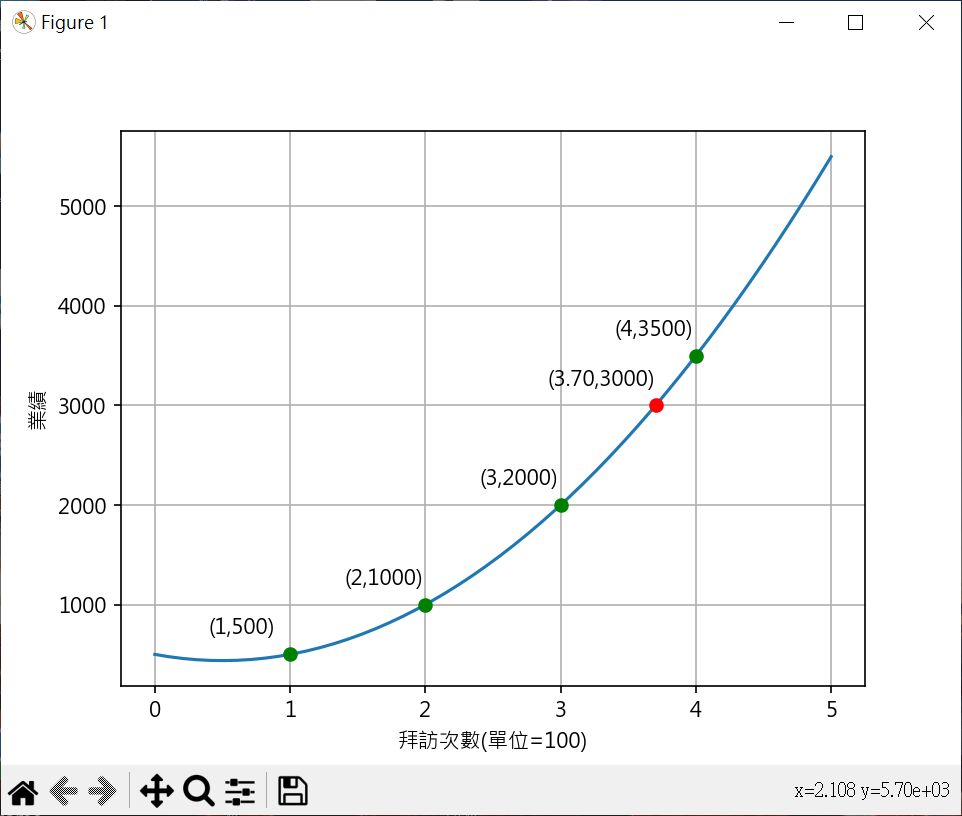
求一元二次方程式,並繪圖 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 from sympy import symbols, solveimport numpy as npimport matplotlib.pyplot as pltplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False def y_count (a, b, c, x ): return (a*x**2 + b*x + c) a, b, c = symbols(("a" , "b" , "c" )) eq1 = a + b + c - 500 eq2 = 4 *a + 2 *b + c - 1000 eq3 = 9 *a + 3 *b + c - 2000 ans = solve((eq1, eq2, eq3)) print (ans)x = np.linspace(0 , 5 , 50 ) y = ans[a]*x**2 + ans[b]*x + ans[c] plt.plot(x,y) for i in range (1 ,5 ): y_axis = y_count(ans[a], ans[b], ans[c], i) plt.plot(i, y_axis, "-o" , color="green" ) plt.text(i - 0.6 , y_axis + 200 , f"({i} ,{y_axis} )" ) from sympy import Symbol, solvecount_value = 3000 z = Symbol("z" ) eq = ans[a]*z**2 + ans[b]*z + ans[c] - count_value ans_3000 = solve(eq) print (ans_3000)for ans_item in ans_3000: ans_value = ans_item.evalf() print (ans_value) if (ans_value > 0 ): plt.plot(ans_value, count_value, "-o" , color="red" ) plt.text(ans_value - 0.8 , count_value + 200 , f"({ans_value:.2 f} ,{count_value} )" ) plt.xlabel('拜訪次數(單位=100)' ) plt.ylabel('業績' ) plt.grid() plt.show()
二次函數的配方法(標準式)
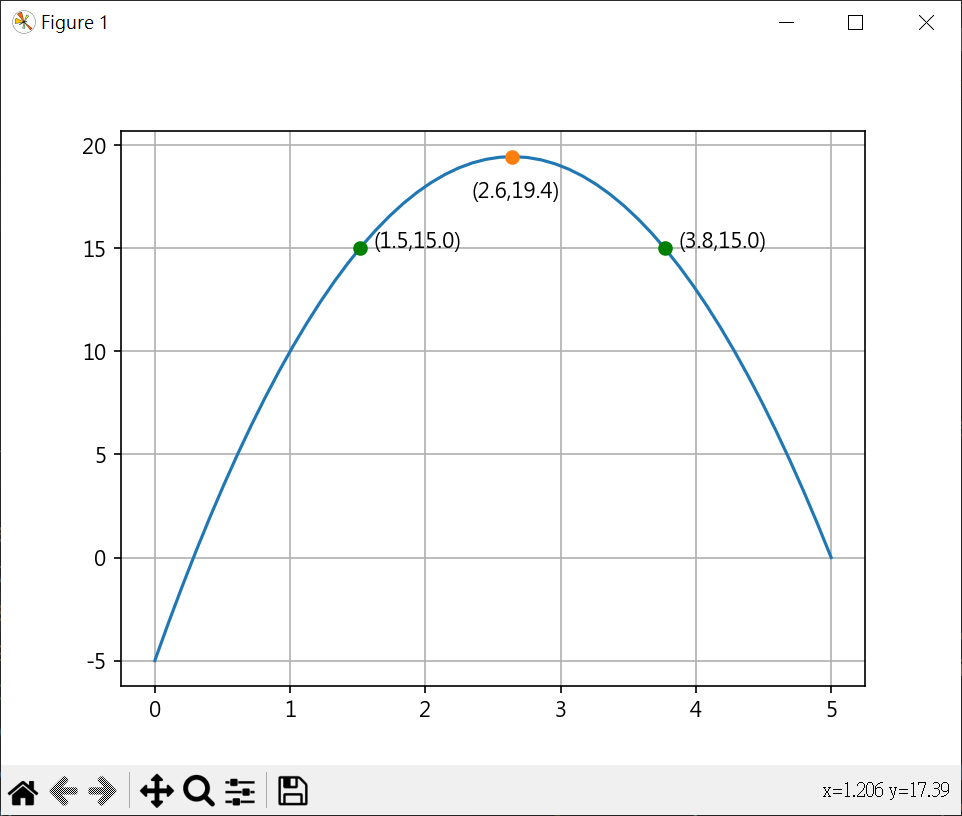
行銷問題分析 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 from sympy import Symbol, symbols, solvea, b, c = symbols(("a" , "b" , "c" )) eq1 = a + b + c - 10 eq2 = 4 *a + 2 *b + c - 18 eq3 = 9 *a + 3 *b + c - 19 ans = solve((eq1, eq2, eq3)) print (ans)def f (x, a, b, c ) : return (a*x**2 + b*x + c) def g (x, a, b, c ) : return -f(x, a, b, c) import matplotlib.pyplot as pltimport numpy as npfrom scipy.optimize import minimize_scalarplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False x = np.linspace(0 , 5 , 50 ) y = ans[a]*x**2 + ans[b]*x + ans[c] plt.plot(x,y) print (ans[a].evalf(), ans[b].evalf(), ans[c].evalf())args = (float (ans[a].evalf()), float (ans[b].evalf()), float (ans[c].evalf())) peak = minimize_scalar(g, args=args) limit_y = -peak.fun print (f"max ({peak.x} ,{limit_y} )" )plt.plot(peak.x,limit_y, "-o" ) plt.text(peak.x-0.3 ,limit_y-2 , f"({peak.x:.1 f} ,{limit_y:.1 f} )" ) ask_y = 15 x2 = Symbol("x2" ) eq = -3.5 *x2**2 + 18.5 *x2 - 20 ans2 = solve(eq) print (ans2)for x_value in ans2: plt.plot(x_value,ask_y, "-o" , color="green" ) plt.text(x_value+0.1 ,ask_y, f"({x_value:.1 f} ,{ask_y:.1 f} )" ) plt.grid() plt.show()
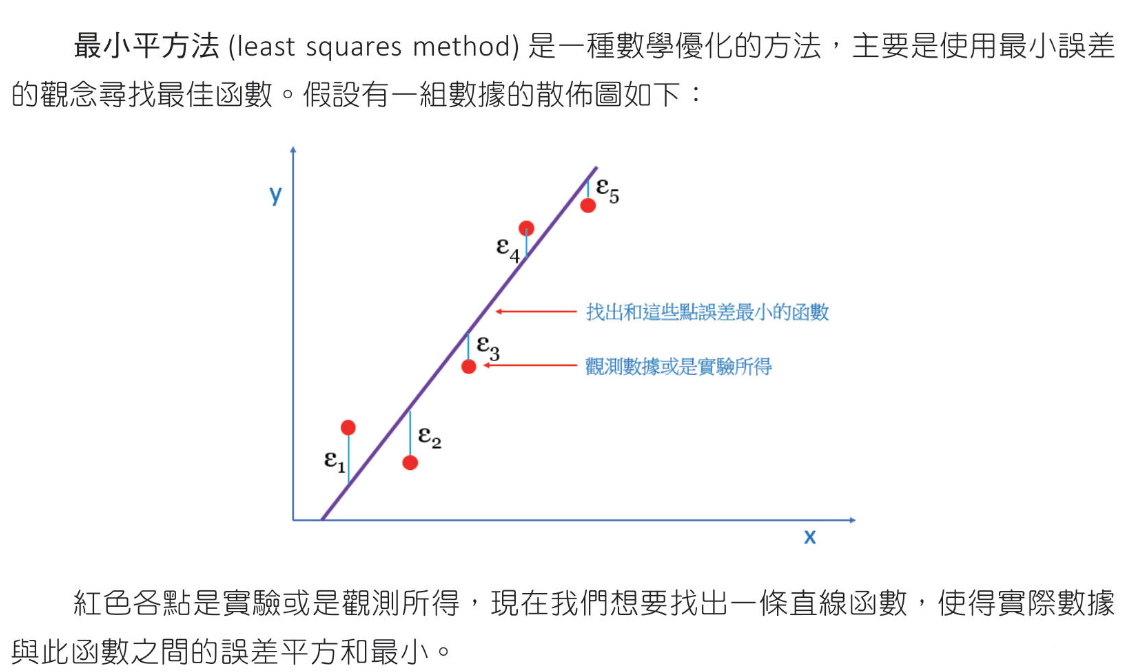
最小平方法(線性迴歸模型)
Numpy 實作最小平方法 # polyfit-計算迴歸線
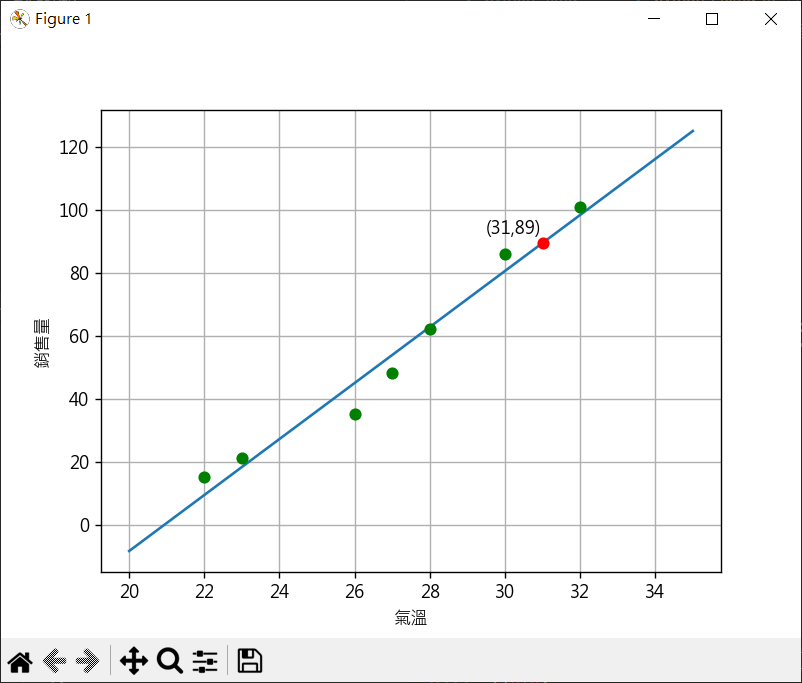
氣溫 vs 銷售量 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 import numpy as npx = np.array([22 , 26 , 23 , 28 , 27 , 32 , 30 ]) y = np.array([15 , 35 , 21 , 62 , 48 , 101 , 86 ]) a, b = np.polyfit(x, y, 1 ) print (f"斜率{a:.2 f} " )print (f"截距{b:.2 f} " )import matplotlib.pyplot as pltplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False x2 = np.linspace(20 , 35 , 50 ) y2 = a * x2 + b plt.plot(x2, y2) x_count = 31 y_count = a*x_count + b plt.plot(x_count, y_count, "-o" , color="red" ) plt.text(x_count-1.5 , y_count+3 , f"({x_count} ,{int (y_count)} )" ) for index, x_value in enumerate (x): plt.plot(x_value, y[index], "-o" , color="green" ) plt.xlabel('氣溫' ) plt.ylabel('銷售量' ) plt.grid() plt.show()
排列與組合 nPr(permutation-排列) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 import itertoolsn = {1 , 2 , 3 , 4 } r = 3 A = set (itertools.permutations(n, r)) print (f"元素數量 = {len (A)} " )for a in A: print (a) n2 = {"a" , "b" , "c" , "d" , "e" } r2 = 2 A2 = set (itertools.permutations(n2, r2)) print (f"元素數量 = {len (A2)} " )for a2 in A2: print (a2)
階層觀念 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 import itertoolsn = {"A" , "B" , "C" , "D" , "E" } r = 5 A = set (itertools.permutations(n, r)) print (f"元素數量 = {len (A)} " )for a in A: print (a) import mathN2 = 30 combinations = math.factorial(N2) print (f"combinations = {combinations} " )times = 10000000000000 years = combinations/times/60 /60 /24 /365 print (f"計算 {years:.2 f} 年" )
重複排列 1 2 3 4 5 6 7 8 9 10 11 12 13 import itertoolsn = {1 , 2 , 3 , 4 , 5 } A = set (itertools.product(n, n , n)) print (f"元素數量 = {len (A)} " )for a in A: print (a)
組合(combination)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import itertoolsn = {1 , 2 , 3 , 4 , 5 } r = 3 A = set (itertools.combinations(n , 3 )) print (f"組合 = {len (A)} " )for a in A: print (a) n2 = {1 , 2 , 3 , 4 , 5 , 6 } A2 = set (itertools.combinations(n2 , 2 )) print (f"骰子組合 = {len (A2)} " )
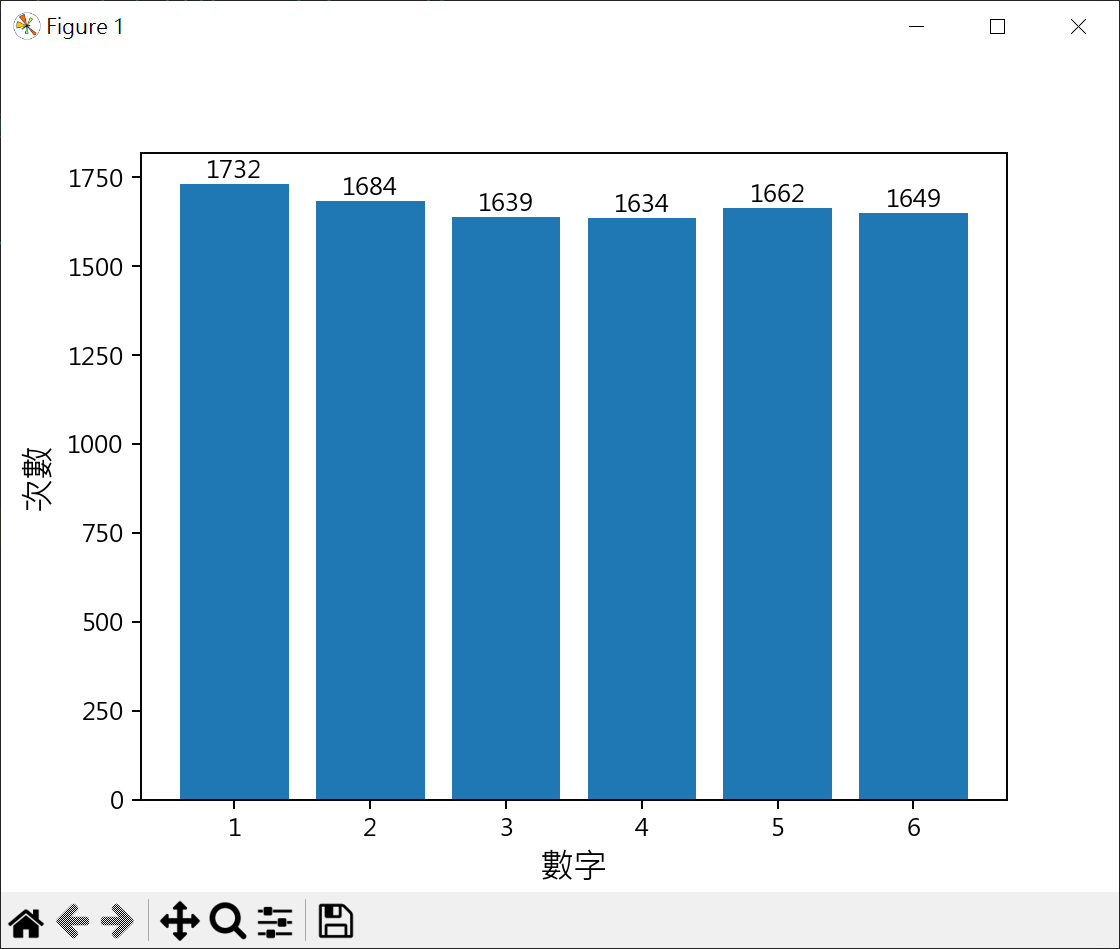
機率 機率基本概念 計算隨機產生值,並繪出長條圖 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 import randommin = 1 max = 6 n = 10000 dice = [0 ] * 6 for i in range (n): data = random.randint(min , max ) dice[data-1 ] += 1 print (dice)import matplotlib.pyplot as pltplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False listx = range (1 ,7 ) plt.bar(listx, dice) plt.xlabel('數字' , fontsize=14 ) plt.ylabel('次數' , fontsize=14 ) for i in range (len (dice)): plt.text(i+1 , dice[i], str (dice[i]), ha='center' , va='bottom' ) plt.show()
機率乘法與加法 1 2 3 4 5 6 7 8 9 10 11 12 13 14 from fractions import Fractionx = Fraction(2 , 7 ) * Fraction(1 ,6 ) y = Fraction(5 , 7 ) * Fraction(2 , 6 ) p = x + y print (f"第一位中獎率 {Fraction(2 , 7 )} " )print (f"第二位中獎率 {p} 轉成浮點數 {float (p)} " )
餘事件與乘法 1 2 3 4 5 6 7 8 9 10 11 12 13 from fractions import Fractionx = Fraction(5 , 6 ) p1 = x**3 p2 = 1 - p1 print (f"不出現5的機率 {float (p1)} " )print (f"出現5的機率 {float (p2)} " )
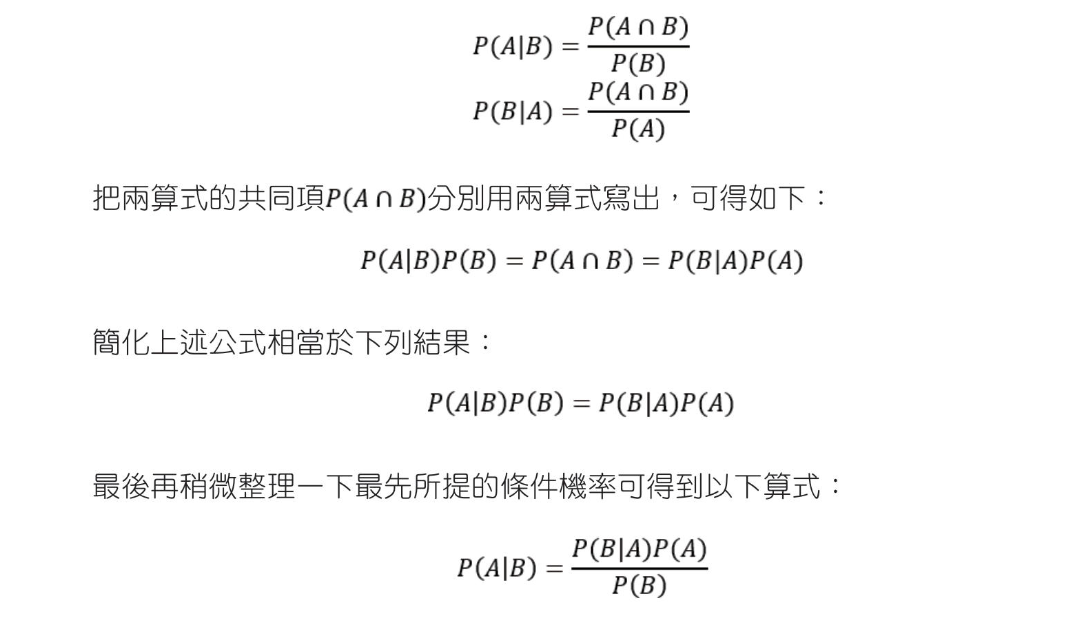
條件機率
貝氏定理
COVID-19 普篩準確度分析 $$P(確診|陽性) = \frac{P(陽性|確診)⋅P(確診)}{P(陽性)} $$快篩
靈敏度(敏感度):99%(即0.99)
假陽性率:1%(即0.01)
先驗患病率:0.01%(即0.0001)
PCR
靈敏度(敏感度):99.99%(即0.9999)
假陽性率:0.01%(即0.0001)
先驗患病率:0.01%(即0.0001)
計算快篩陽性確診率 0.01 0.0001/0.010098 = 0.0098
計算PCR陽性確診率 0.0001 0.0001/0.00019998 = 0.5
結果
快篩陽性結果確診率:約0.98%
PCR陽性結果確診率 :約50%
快篩即使測試具有高靈敏度和特異性,當患病率非常低時,假陽性結果仍會顯著影響快篩測試的後驗概率,而PCR測試在低患病率的情況下能提供更準確的後驗概率。
醫學例子分析 某疾病測試,對有疾病測出有真陽性為99%,對無疾病測出真陰性為99%,假設在某群體中,有疾病的機率為1%0.01 0.01/0.0198 = 0.5
1 2 3 4 5 6 7 8 P_A = 0.01 P_B_given_A = 0.99 P_B = 0.01 *0.99 + (1 - 0.01 )*0.01 P_A_given_B = P_B_given_A * P_A / P_B print (f"陽性有疾病的機率 {P_A_given_B} " )
垃圾郵件分類實作 $$P(spam∣words) = \frac{P(words∣spam)⋅P(spam)}{P(words)} $$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 import numpy as npspam_emails = [ "Get a free gift card now!" , "Limited time offer: Claim your prize!" , "You have won a free iPhone!" ] ham_emails = [ "Meeting rescheduled for tomorrow" , "Can we discuss the repoet later?" , "Thank you for your prompt reply." ] def count_words (emails ): word_count= {} for email in emails: for word in email.split(): word = word.lower() if word not in word_count: word_count[word] = 1 else : word_count[word] += 1 return word_count def classify_email (email ): words = email.lower().split() spam_prob = np.log(prior_spam) ham_prob = np.log(prior_ham) for word in words: spam_prob += np.log(spam_word_prob.get(word, 1 / (total_spam_words+2 ))) ham_prob += np.log(ham_word_prob.get(word, 1 / (total_ham_words+2 ))) print (f"spam_prob:{spam_prob} ham_prob:{ham_prob} " ) return "垃圾郵件" if spam_prob > ham_prob else "非垃圾郵件" def word_probability (word_count, total_count ): return {word:(count+1 )/(total_count+2 ) for word, count in word_count.items()} prior_spam = len (spam_emails) / (len (spam_emails) + len (ham_emails)) prior_ham = len (ham_emails) / (len (spam_emails) + len (ham_emails)) print (f"垃圾郵件先驗機率:{prior_spam} " )print (f"正常郵件先驗機率:{prior_ham} " )print ("=" *70 )spam_word_count = count_words(spam_emails) ham_word_count = count_words(ham_emails) print (f"垃圾郵件單詞:{spam_word_count} " )print (f"正常郵件單詞:{ham_word_count} " )print ("=" *70 )total_spam_words = sum (spam_word_count.values()) total_ham_words = sum (ham_word_count.values()) print (f"垃圾郵件總單詞:{total_spam_words} " )print (f"正常郵件總單詞:{total_ham_words} " )print ("=" *70 )spam_word_prob = word_probability(spam_word_count, total_spam_words) ham_word_prob = word_probability(ham_word_count, total_ham_words) print (f"垃圾郵件字典單詞機率:{spam_word_prob} " )print (f"正常郵件字典單詞機率:{ham_word_prob} " )print ("=" *70 )test_email = "Claims your free gift now" print (f"郵件:{test_email} 分類結果:{classify_email(test_email)} " )test_email = "Can we discuss your decision tomorrow" print (f"郵件:{test_email} 分類結果:{classify_email(test_email)} " )
蒙地卡羅模擬計算PI 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import randomtrials = 1000000 hits = 0 for i in range (trials): x = random.random()*2 - 1 y = random.random()*2 - 1 if x*x + y*y <= 1 : hits += 1 PI = 4 * hits / trials print (f"PI={PI} " )
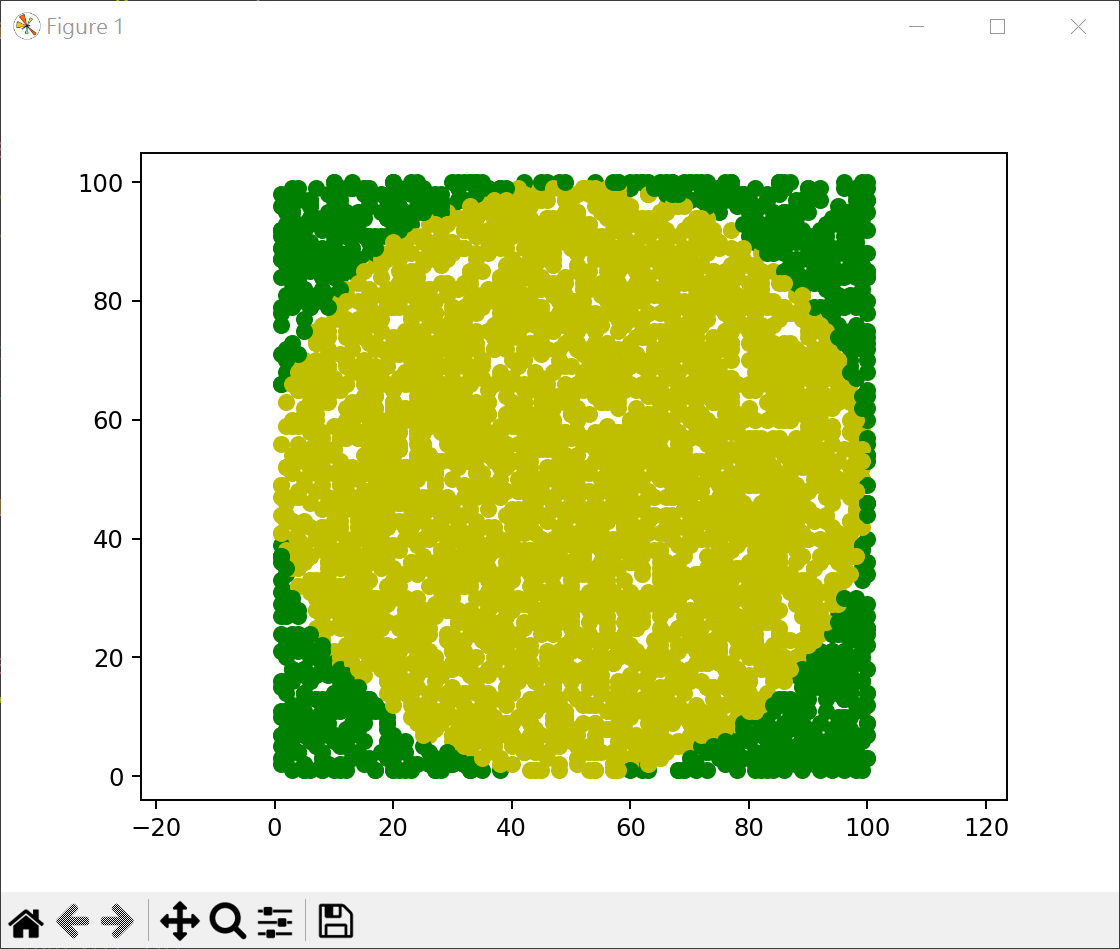
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 import matplotlib.pyplot as pltimport randomimport mathtrials = 5000 hits = 0 radius = 50 for i in range (trials) : x = random.randint(1 , 100 ) y = random.randint(1 , 100 ) if math.sqrt((x-50 )**2 + (y-50 )**2 ) <= radius: plt.plot(x, y, "-o" , c="y" ) hits += 1 else : plt.plot(x, y, "-o" , c="g" ) PI = 4 * hits / trials print (f"PI={PI} " )plt.axis('equal' ) plt.show()
二項式定理 二項式定理主要是講解二項式次方的展開 $(x+y)^n$
二項式展開與規律性
找出 $x^{n-k}y^k$ 係數 二項式定理如下:
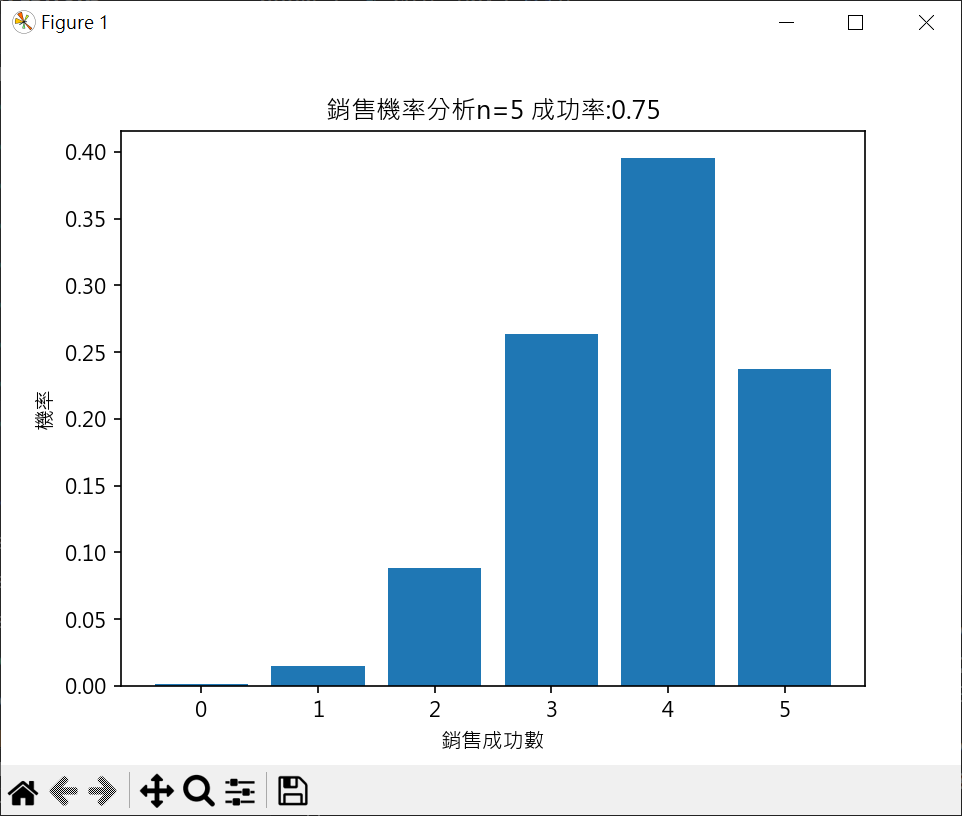
二項式應用於業務分析 假設推銷成功率為0.75(所以失敗率為0.25)
5次銷售皆失敗的機率 x 表成功次數
僅1次銷售成功的機率 $ P(x=1)=\left( ^5_1\right)(0.75)(0.25)^4=5(0.75)(0.25)^4=0.0146484375=1.46484375\% $
僅2次銷售成功的機率 $ P(x=2)=\left( ^5_2\right)(0.75)^2(0.25)^3=10(0.75)^2(0.25)^3=0.087890625=8.7890625\% $
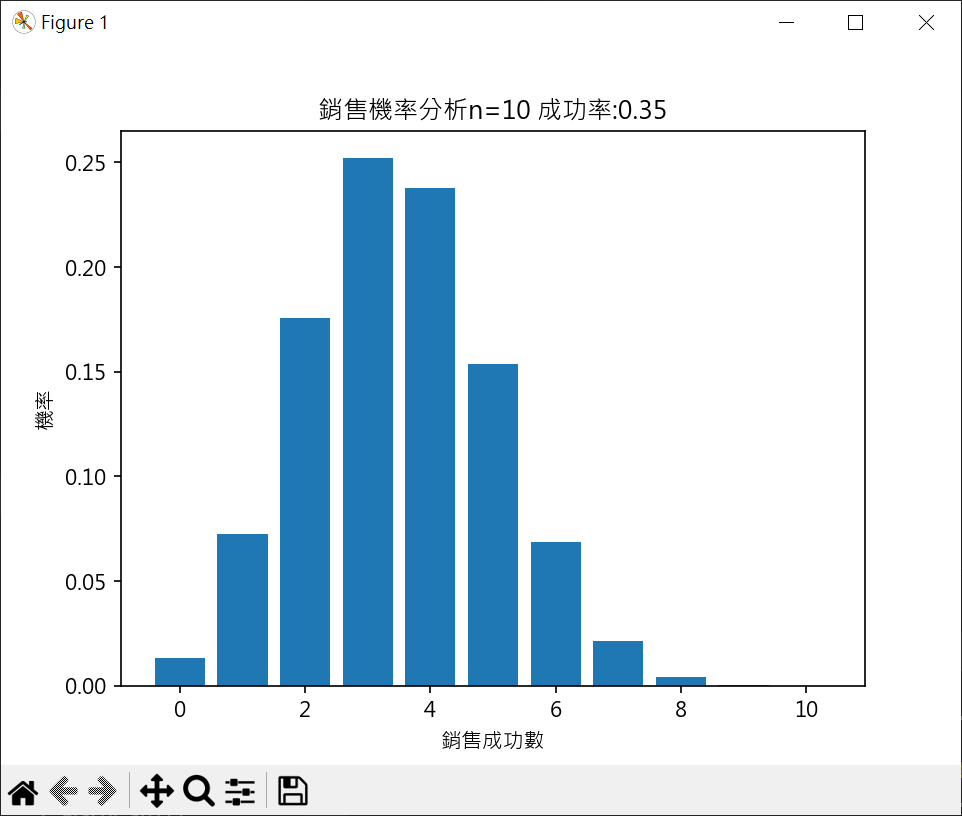
業務分析機率計算集繪製長條圖 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 import matplotlib.pyplot as pltimport mathplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False def probability (k ): num = math.factorial(n)/(math.factorial(k)*math.factorial(n-k)) return num*success**(k)*fail**(n-k) n = 5 success = 0.75 fail = 1 - success p = [] for k in range (0 ,n+1 ): if k == 0 : p.append(fail**n) elif k == n: p.append(success**n) else : p.append(probability(k)) print (p)listx = [i for i in range (0 ,n+1 ) ] plt.bar(listx, p) plt.title(f'銷售機率分析n={n} 成功率:{success} ' ) plt.xlabel('銷售成功數' ) plt.ylabel('機率' ) plt.show()
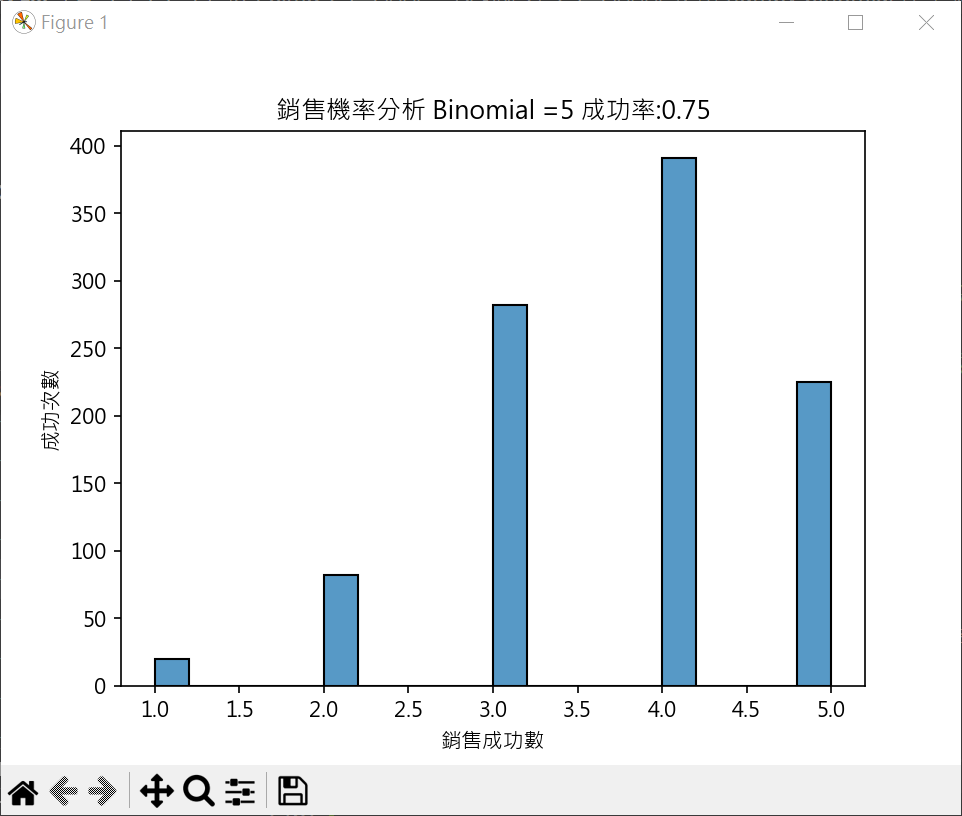
使用 numpy binomial 產生業務分析資料繪圖 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 import matplotlib.pyplot as pltimport numpy as npimport seaborn as snsplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] n = 5 success = 0.75 samples = np.random.binomial(n=n , p=success, size=1000 ) sns.histplot(samples, kde=False ) plt.title(f'銷售機率分析 Binomial ={n} 成功率:{success} ' ) plt.xlabel('銷售成功數' ) plt.ylabel('成功次數' ) plt.show()
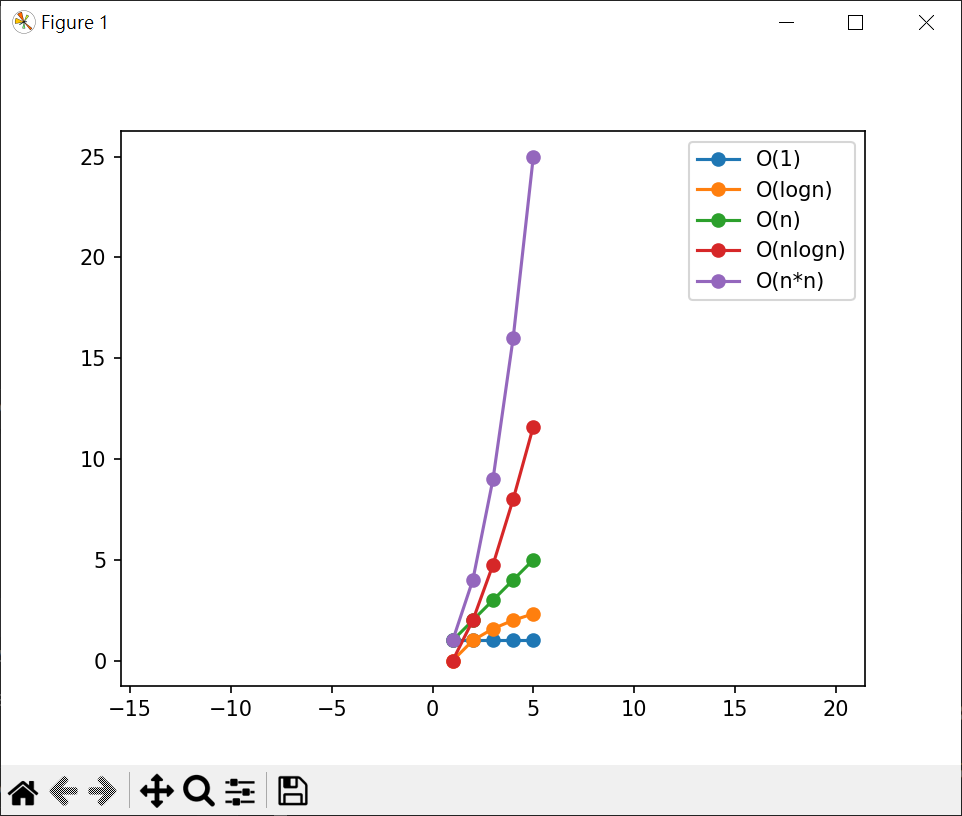
指數 繪製執行時間關係圖(n=1~5) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 import matplotlib.pyplot as pltimport numpy as npxpt = np.linspace(1 ,5 ,5 ) print (xpt)ypt1 = xpt / xpt ypt2 = np.log2(xpt) ypt3 = xpt ypt4 = xpt*np.log2(xpt) ypt5 = xpt*xpt print (ypt1)print (ypt2)print (ypt3)print (ypt4)print (ypt5)plt.plot(xpt, ypt1, '-o' , label="O(1)" ) plt.plot(xpt, ypt2, '-o' , label="O(logn)" ) plt.plot(xpt, ypt3, '-o' , label="O(n)" ) plt.plot(xpt, ypt4, '-o' , label="O(nlogn)" ) plt.plot(xpt, ypt5, '-o' , label="O(n*n)" ) plt.legend(loc="best" ) plt.axis("equal" ) plt.show()
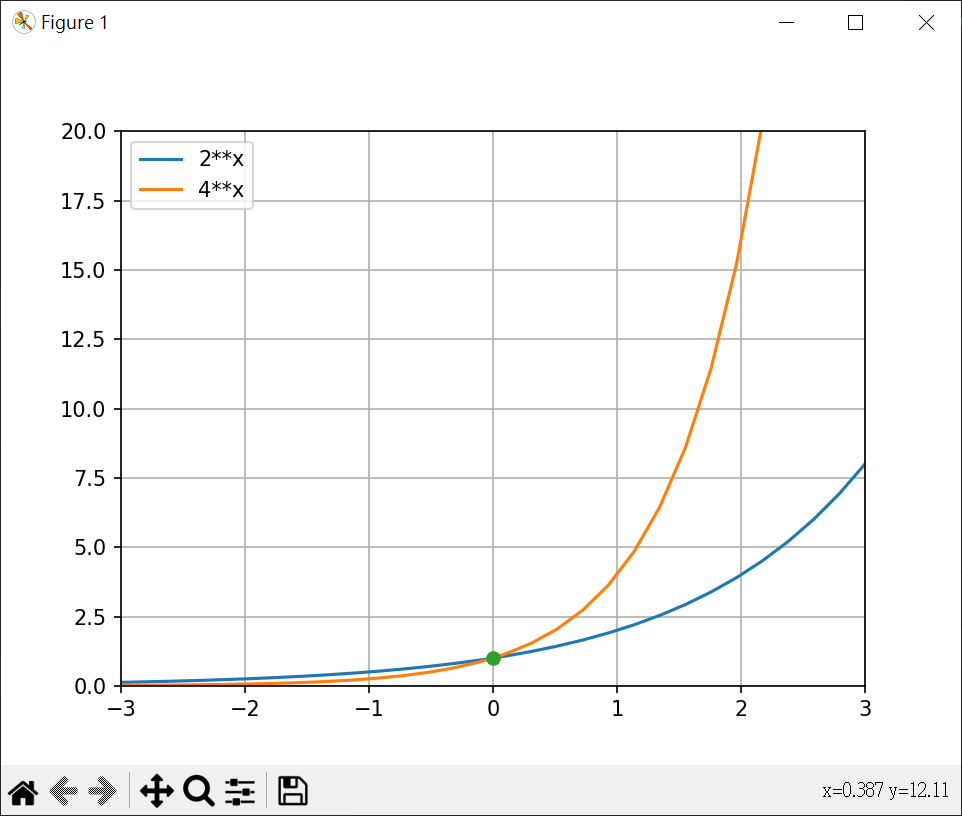
繪製 $y=2^x, y=4^x$ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import matplotlib.pyplot as pltimport numpy as npx = np.linspace(-3 , 3 , 30 ) y2 = 2 ** x y4 = 4 ** x plt.plot(x, y2, label="2**x" ) plt.plot(x, y4, label="4**x" ) plt.plot(0 , 1 , '-o' ) plt.legend(loc="best" ) plt.axis([-3 , 3 , 0 , 20 ]) plt.grid() plt.show()
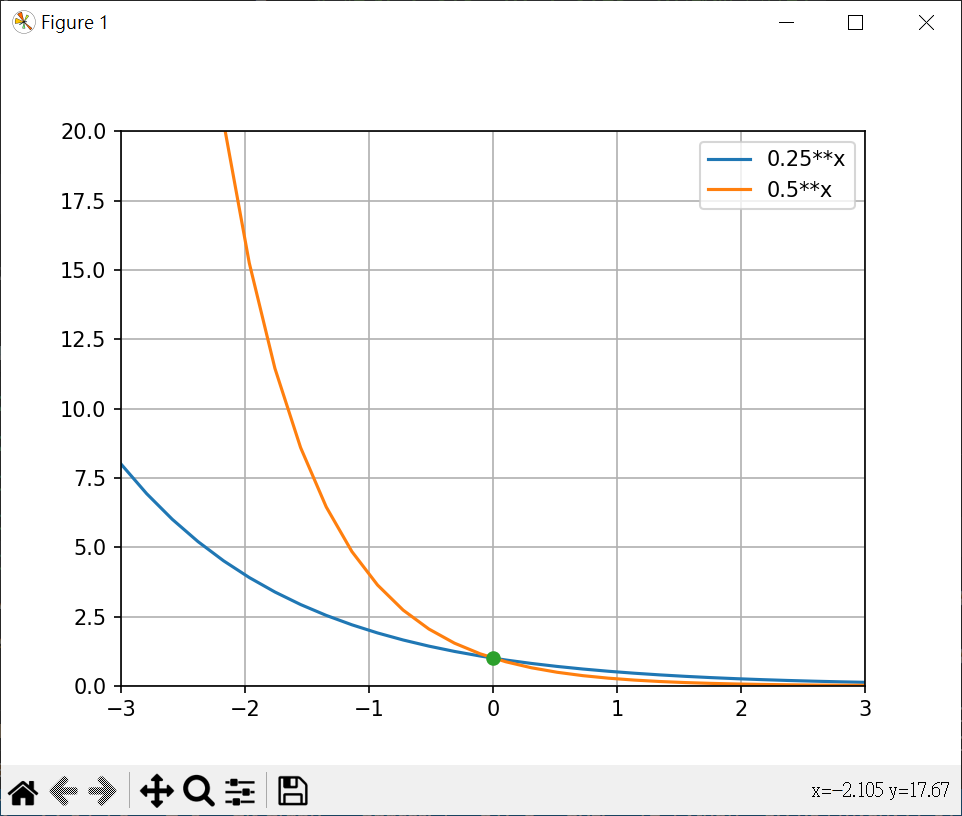
繪製 $y=0.5^x, y=0.25^x$ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import matplotlib.pyplot as pltimport numpy as npx = np.linspace(-3 , 3 , 30 ) y2 = 0.5 ** x y4 = 0.25 ** x plt.plot(x, y2, label="0.25**x" ) plt.plot(x, y4, label="0.5**x" ) plt.plot(0 , 1 , '-o' ) plt.legend(loc="best" ) plt.axis([-3 , 3 , 0 , 20 ]) plt.grid() plt.show()
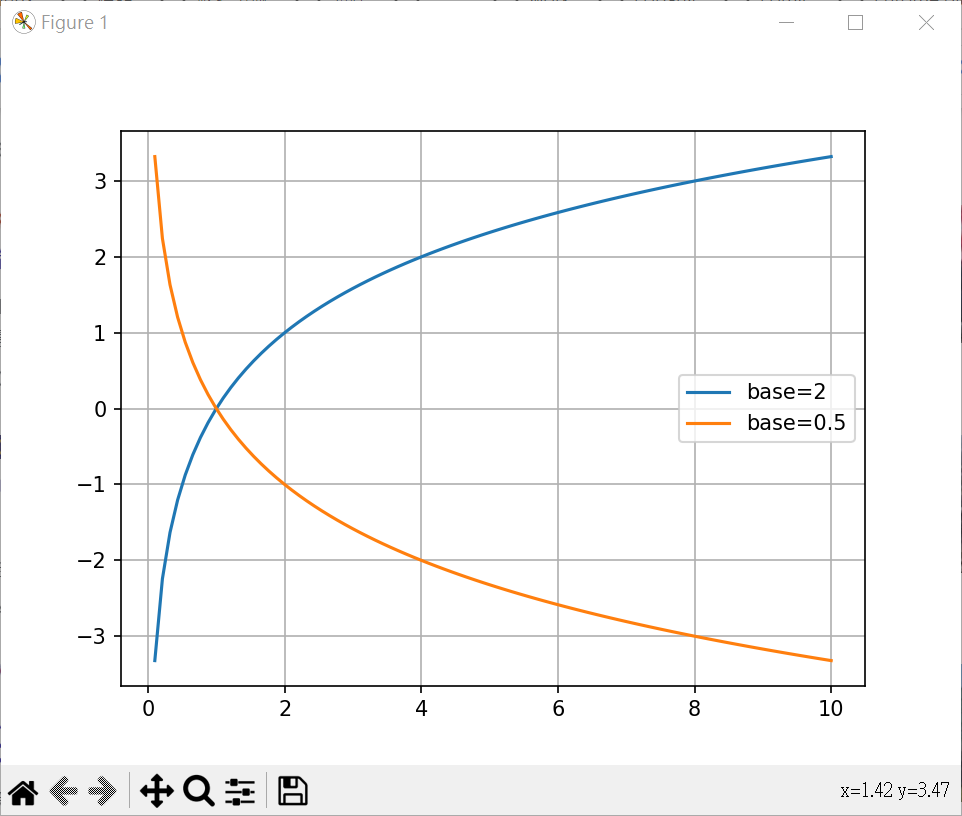
對數 繪對數 2 及 0.5 的圖形 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import matplotlib.pyplot as pltimport numpy as npimport mathx1 = np.linspace(0.1 , 10 , 90 ) y1 = [math.log2(x) for x in x1 ] y2 = [math.log(x, 0.5 ) for x in x1 ] print (y1)print (y2)plt.plot(x1, y1, label="base=2" ) plt.plot(x1, y2, label="base=0.5" ) plt.legend(loc="best" ) plt.grid() plt.show()
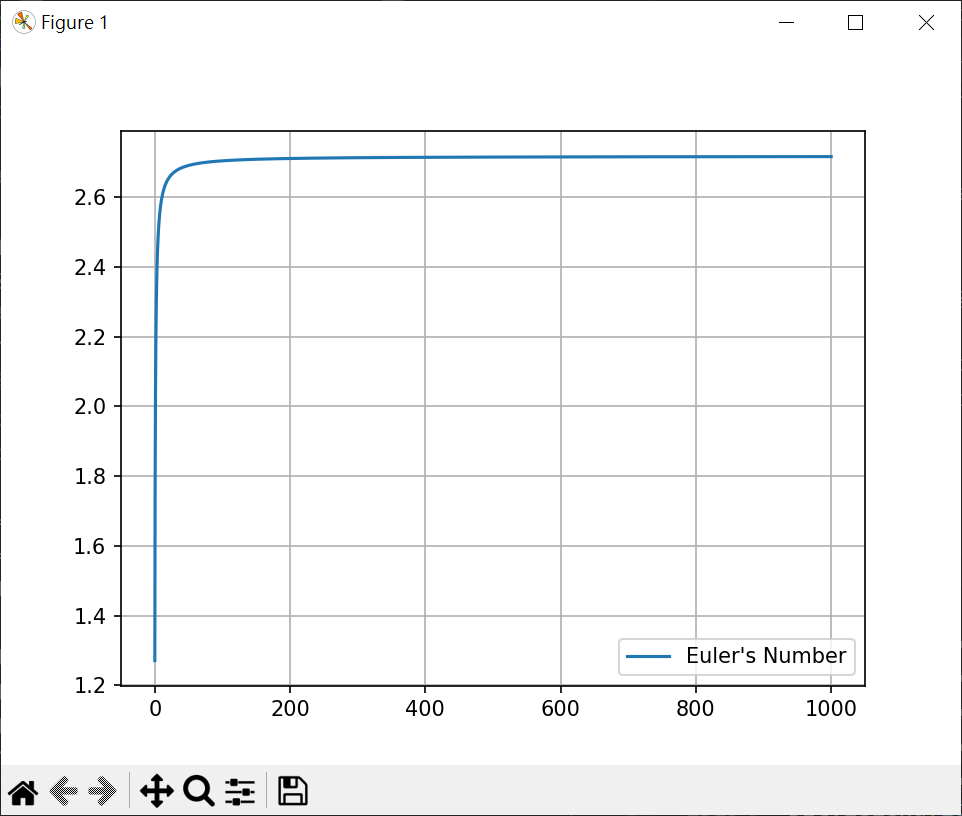
歐拉數與邏輯函數 歐拉數-Euler’s Number $$ 歐拉數 e = \lim_{n \to \infty}\left( 1+\frac{1}{n} \right)^n \approx 2.718281778… $$
繪製歐拉數圖形 1 2 3 4 5 6 7 8 9 10 11 import matplotlib.pyplot as pltimport numpy as npx = np.linspace(0.1 , 1000 , 100000 ) y = [(1 +1 /x)**x for x in x] plt.plot(x, y, label="Euler's Number" ) plt.legend(loc="best" ) plt.grid() plt.show()
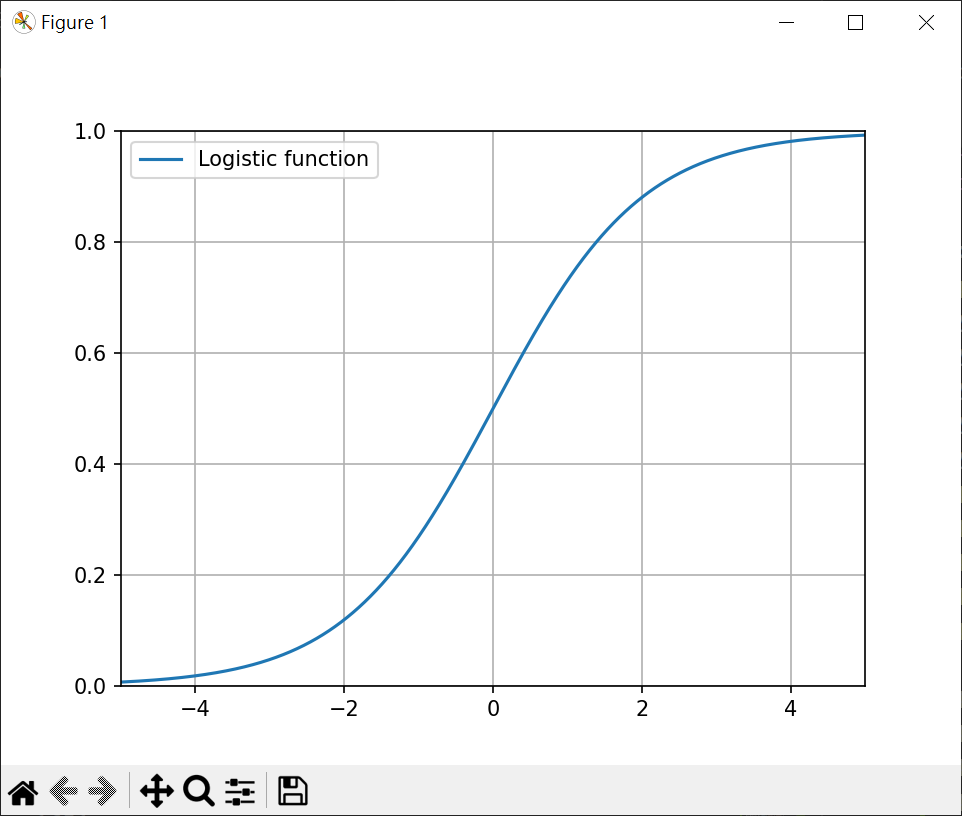
邏輯函數(logistic function) 邏輯函數是一種常見的S(Sigmoid)函數值介於0~1之間,簡單邏輯函數定義如下
繪製邏輯函數 1 2 3 4 5 6 7 8 9 10 11 import matplotlib.pyplot as pltimport numpy as npx = np.linspace(-5 , 5 , 10000 ) y = [1 /(1 +np.e**-x) for x in x] plt.plot(x, y, label="Logistic function" ) plt.axis([-5 , 5 , 0 , 1 ]) plt.legend() plt.grid() plt.show()
Sigmoid 函數
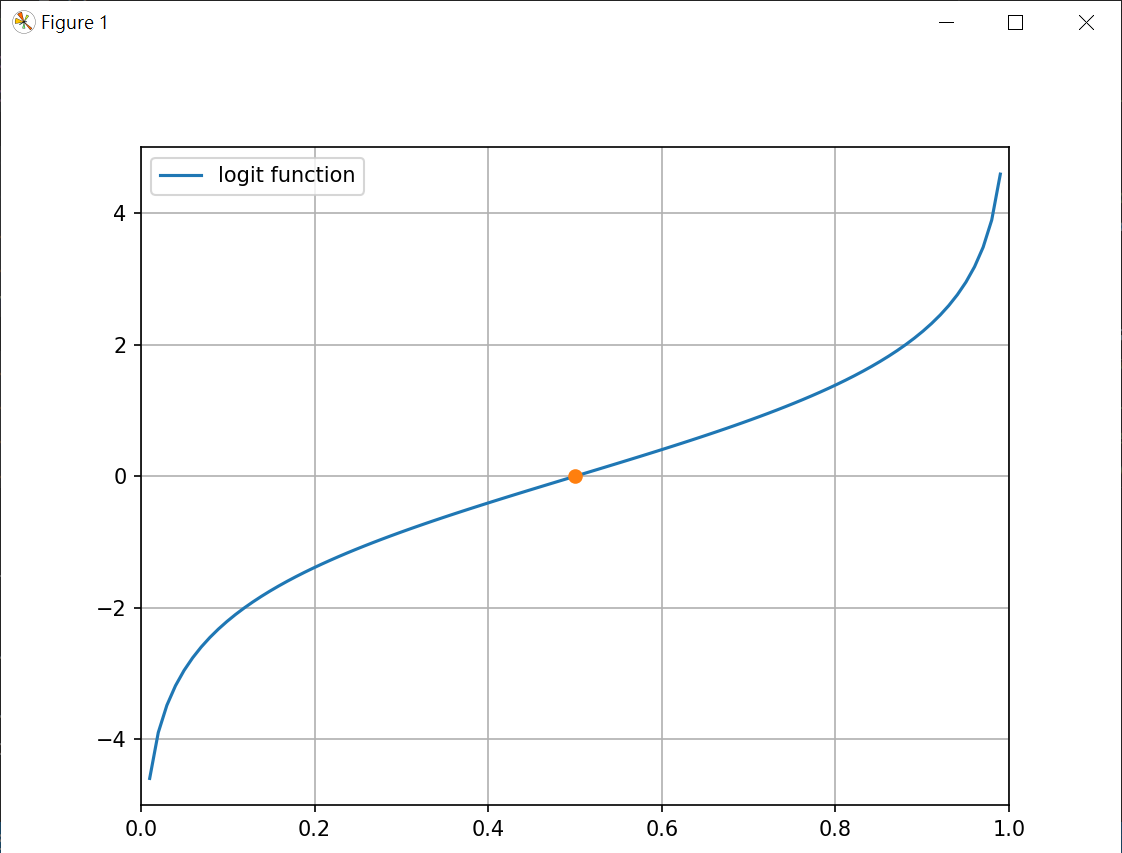
logit 函數 logit是logistic的反函數,它將(0,1)區間數值轉為實數全域,讓我們可以將機率數值轉成實數,進行數學操作
Odds Odds可翻譯為勝率,優勢比或賠率
Odds 到 logit logit 就是 log of Odds(log 底數為 e)
繪製 logit 函數 1 2 3 4 5 6 7 8 9 10 11 12 13 14 import matplotlib.pyplot as pltimport numpy as npx = np.linspace(0.01 , 0.99 , 100 ) y = [np.log(x/(1 -x)) for x in x] plt.plot(x, y, label="logit function" ) plt.plot(0.5 , np.log(0.5 /(1 -0.5 )), "-o" ) print (np.log(0.5 /(1 -0.5 )))plt.axis([0 , 1 , -5 , 5 ]) plt.legend() plt.grid() plt.show()
推算出錯率與回購率的關係 無出錯回購率40%
無出錯賠率和對數賠率
1次錯賠率和對數賠率
logist模型設定
預測2次錯回購率 計算對數賠率 轉換為賠率 轉換為回購率
三角函數
角度弧度的換算 1 2 3 4 5 6 7 8 9 10 11 12 13 14 import numpy as npdegrees = [30 , 45 , 60 , 90 , 120 , 135 , 150 , 180 ] for degree in degrees: print (f"角度={degree} 弧度={np.pi*degree/180 :.3 f} " )
計算弧長 1 2 3 4 5 6 7 8 9 10 11 12 import numpy as npr = 10 degrees = [30 , 60 , 90 , 120 ] for degree in degrees: print (f"角度={degree:3d} 弧長={2 *np.pi*r*degree/360 :.3 f} " )
計算sin(), cos() 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 import numpy as npdegrees = [x*30 for x in range (0 ,13 )] for d in degrees: rad = np.radians(d) sin = np.sin(rad) cos = np.cos(rad) print (f"度數:{d:3d} \t弧度:{rad:3.2 f} \tsin{d:3d} ={sin:3.2 f} cos{d:3d} ={cos:3.2 f} " )
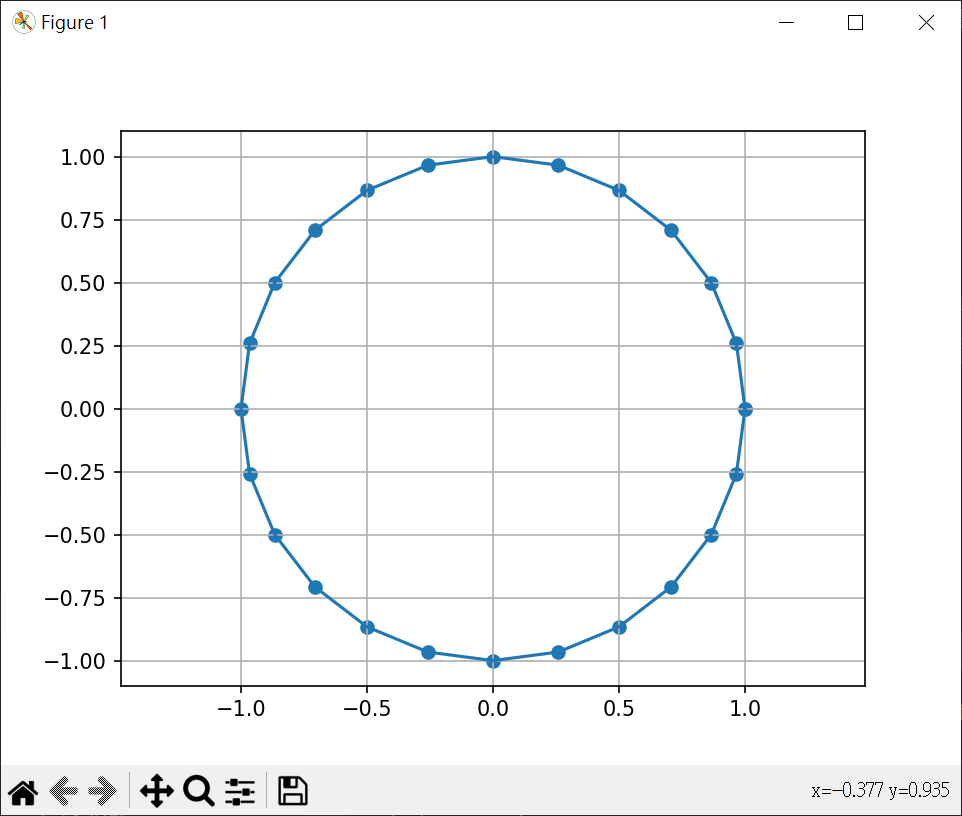
角度繪圓 1 2 3 4 5 6 7 8 9 10 11 12 13 14 import matplotlib.pyplot as pltimport mathdegrees = [x*15 for x in range (0 ,25 )] x = [math.cos(math.radians(d)) for d in degrees] y = [math.sin(math.radians(d)) for d in degrees] plt.scatter(x, y) plt.plot(x,y) plt.axis("equal" ) plt.grid() plt.show()
產生一年的 sin, cos 值 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 import pandas as pdimport numpy as npdates = pd.date_range(start="2023-01-01" , end="2023-12-31" ) df = pd.DataFrame(data={'date' :dates}) df['day_of_year' ] = df['date' ].dt.day_of_year df["sin_day_of_year" ] = np.sin(2 *np.pi*df["day_of_year" ]/365 ) df["cos_day_of_year" ] = np.cos(2 *np.pi*df["day_of_year" ]/365 ) print (df)
基礎統計與大型運算子 數據中心指標 平均數(mean)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 import numpy as npimport statistics as stx = [66 , 57 , 25 , 80 , 60 , 15 , 120 , 39 , 80 , 50 ] x2 = [66 , 57 , 25 , 80 , 60 , 15 , 120 , 39 , 80 , 50 , 77 ] print (f"加總: {sum (x)} " )print (f"平均數: {sum (x)/len (x)} " )print (f"平均數2: {np.mean(x)} " )print (f"中位數: {np.median(x)} " )print (f"中位數2: {np.median(x2)} " )print (f"x bincount : {len (np.bincount(x))} " )print (f"x2 bincount : {len (np.bincount(x2))} " )print (f"x argmax : {np.argmax(x)} {x[np.argmax(x)]} " )print (f"x2 argmax : {np.argmax(x2)} {x2[np.argmax(x)]} " )print (f"x argmin : {np.argmin(x)} {x[np.argmin(x)]} " )print (f"x2 argmin : {np.argmin(x2)} {x2[np.argmin(x)]} " )print (f"x mode:{st.mode(x)} " )
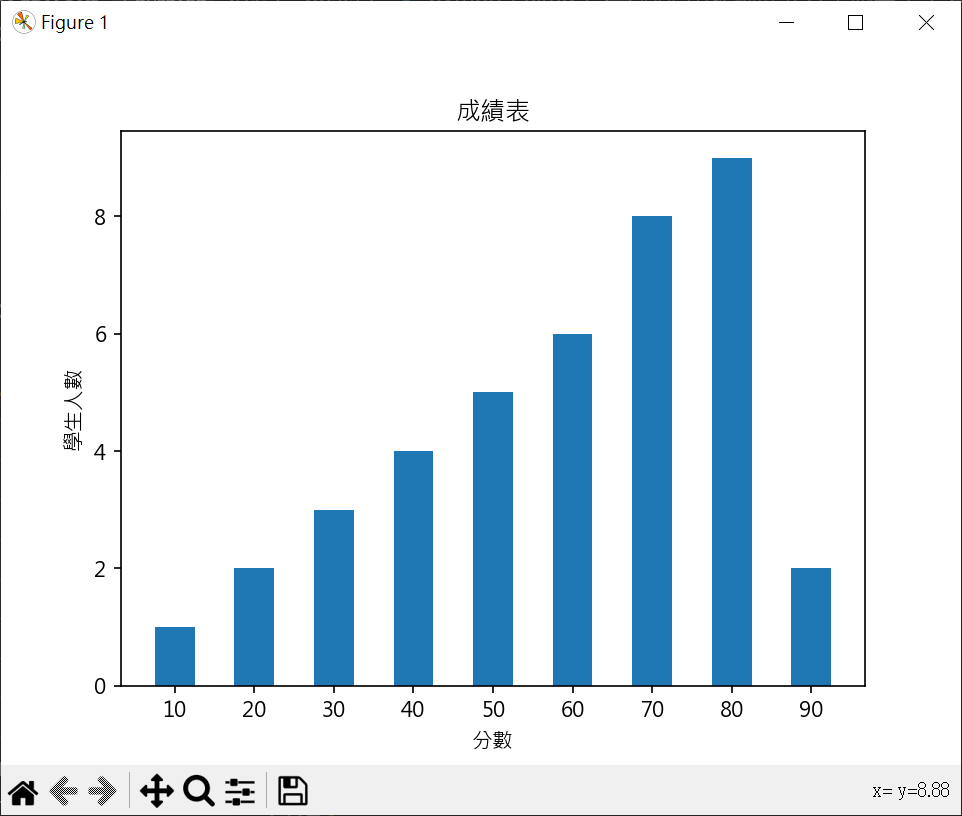
繪製成績分布圖 繪製成績長條圖 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 import matplotlib.pyplot as pltimport numpy as npimport statistics as stplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] sc = [60 ,10 ,40 ,80 ,80 ,30 ,80 ,60 ,70 ,90 ,50 ,50 ,50 ,70 ,60 ,80 ,80 ,50 ,60 ,70 , 70 ,40 ,30 ,70 ,60 ,80 ,20 ,80 ,70 ,50 ,90 ,80 ,40 ,40 ,70 ,60 ,80 ,30 ,20 ,70 ] print (f"平均成績 = {np.mean(sc)} " )print (f"中位數成績 = {np.median(sc)} " )print (f"眾數成績 = {st.mode(sc)} " )hist = [0 ] * 9 for s in sc : n = int (s/10 ) - 1 hist[n] += 1 x = np.arange(len (hist)) plt.bar(x, hist, width=0.5 ) plt.xticks(x, (10 ,20 ,30 ,40 ,50 ,60 ,70 ,80 ,90 )) plt.title("成績表" ) plt.xlabel("分數" ) plt.ylabel("學生人數" ) plt.show()
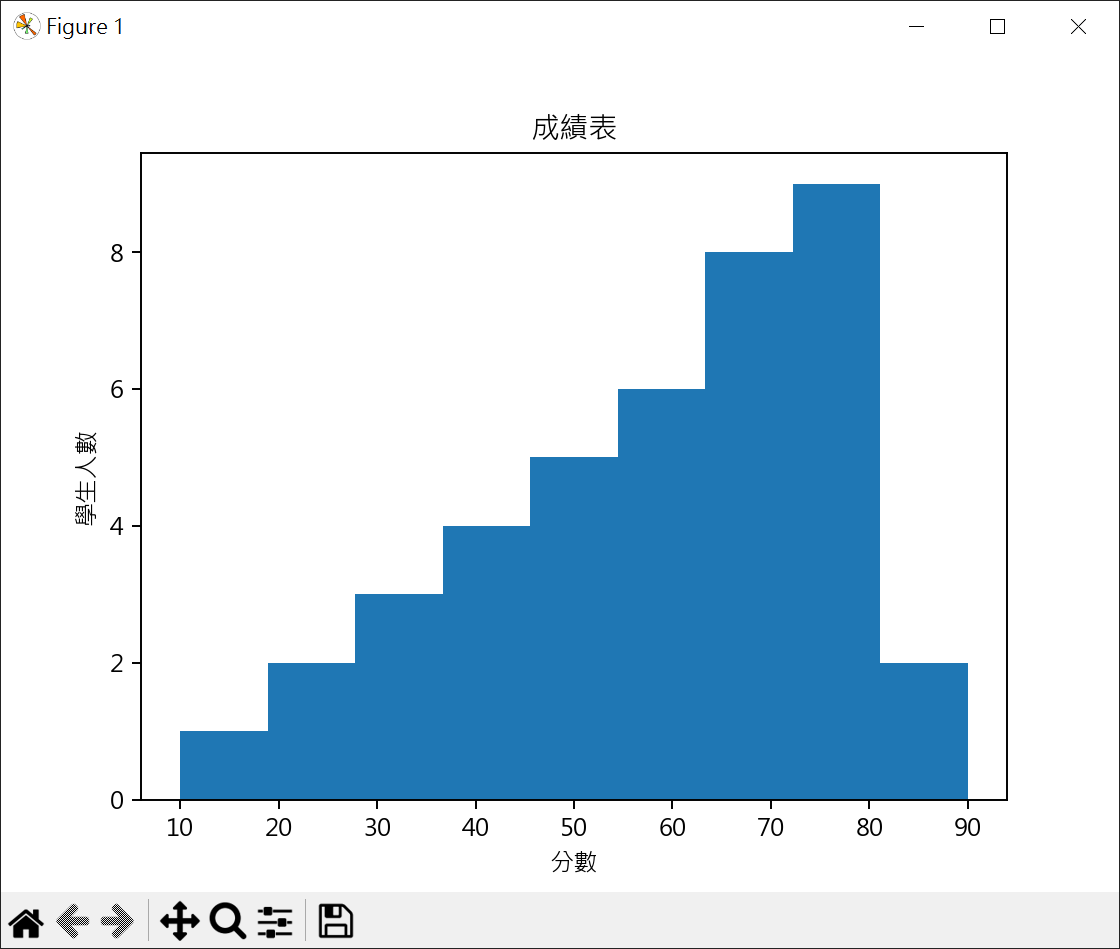
繪製成績直方圖 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 import matplotlib.pyplot as pltimport numpy as npimport statistics as stplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] sc = [60 ,10 ,40 ,80 ,80 ,30 ,80 ,60 ,70 ,90 ,50 ,50 ,50 ,70 ,60 ,80 ,80 ,50 ,60 ,70 , 70 ,40 ,30 ,70 ,60 ,80 ,20 ,80 ,70 ,50 ,90 ,80 ,40 ,40 ,70 ,60 ,80 ,30 ,20 ,70 ] plt.hist(sc, 9 ) plt.title("成績表" ) plt.xlabel("分數" ) plt.ylabel("學生人數" ) plt.show()
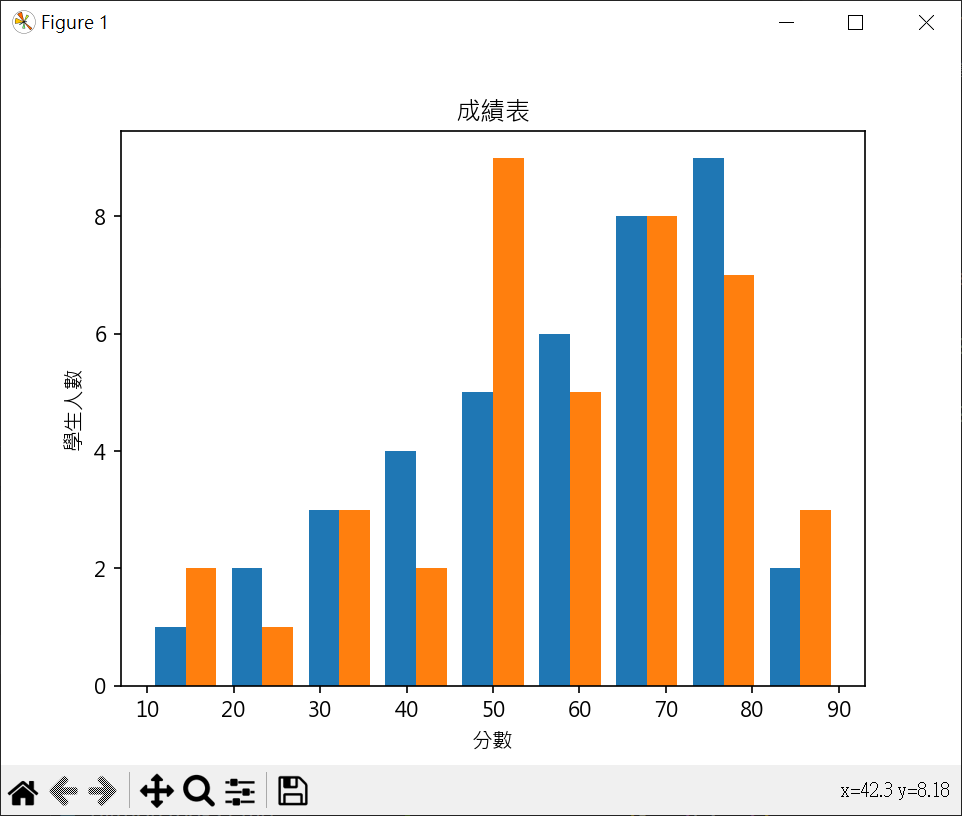
繪製成績直方圖(兩個成績) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 import matplotlib.pyplot as pltimport numpy as npimport statistics as stplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] sc1 = [60 ,10 ,40 ,80 ,80 ,30 ,80 ,60 ,70 ,90 ,50 ,50 ,50 ,70 ,60 ,80 ,80 ,50 ,60 ,70 , 70 ,40 ,30 ,70 ,60 ,80 ,20 ,80 ,70 ,50 ,90 ,80 ,40 ,40 ,70 ,60 ,80 ,30 ,20 ,70 ] sc2 = [50 ,10 ,60 ,80 ,70 ,30 ,80 ,60 ,30 ,90 ,50 ,50 ,50 ,90 ,70 ,60 ,50 ,80 ,50 ,70 , 60 ,50 ,30 ,70 ,70 ,80 ,10 ,80 ,70 ,50 ,90 ,80 ,40 ,50 ,70 ,60 ,80 ,40 ,20 ,70 ] plt.hist([sc1, sc2], 9 ) plt.title("成績表" ) plt.xlabel("分數" ) plt.ylabel("學生人數" ) plt.show()
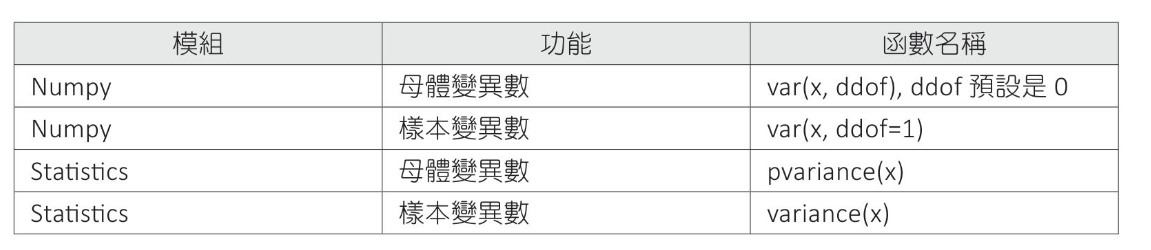
數據分散指標 變異數 母體變異數 樣本變異數 變異數公式
計算銷售數據變異數
1 2 3 4 5 6 7 8 9 10 11 12 import numpy as npimport statistics as stx = [66 , 58 , 25 , 78 , 58 , 15 , 120 , 39 , 82 , 50 ] print (f"Numpy 母體變異數 : {np.var(x):6.2 f} " )print (f"Numpy 樣本變異數 : {np.var(x, ddof=1 ):6.2 f} " )print (f"Statistics 母體變異數: {st.pvariance(x):6.2 f} " )print (f"Statistics 樣本變異數: {st.variance(x):6.2 f} " )
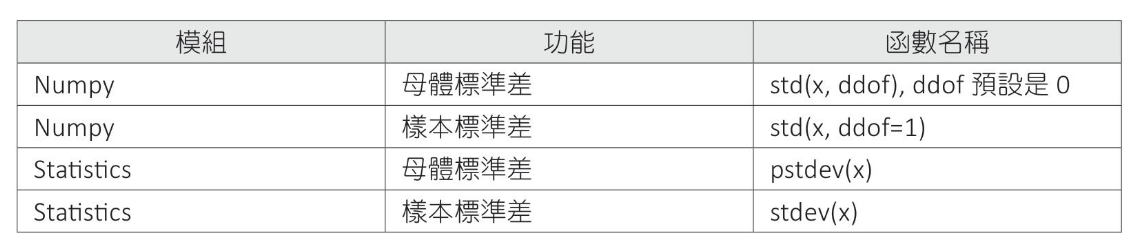
標準差(Standard Deviation-SD) 變異數開根號就是標準差母體標準差 樣本標準差 標準差公式
計算銷售數據標準差
1 2 3 4 5 6 7 8 9 10 11 12 import numpy as npimport statistics as stx = [66 , 58 , 25 , 78 , 58 , 15 , 120 , 39 , 82 , 50 ] print (f"Numpy 母體標準差 : {np.std(x):.2 f} " )print (f"Numpy 樣本標準差 : {np.std(x, ddof=1 ):.2 f} " )print (f"Statistics 母體標準差: {st.pstdev(x):.2 f} " )print (f"Statistics 樣本標準差: {st.stdev(x):.2 f} " )
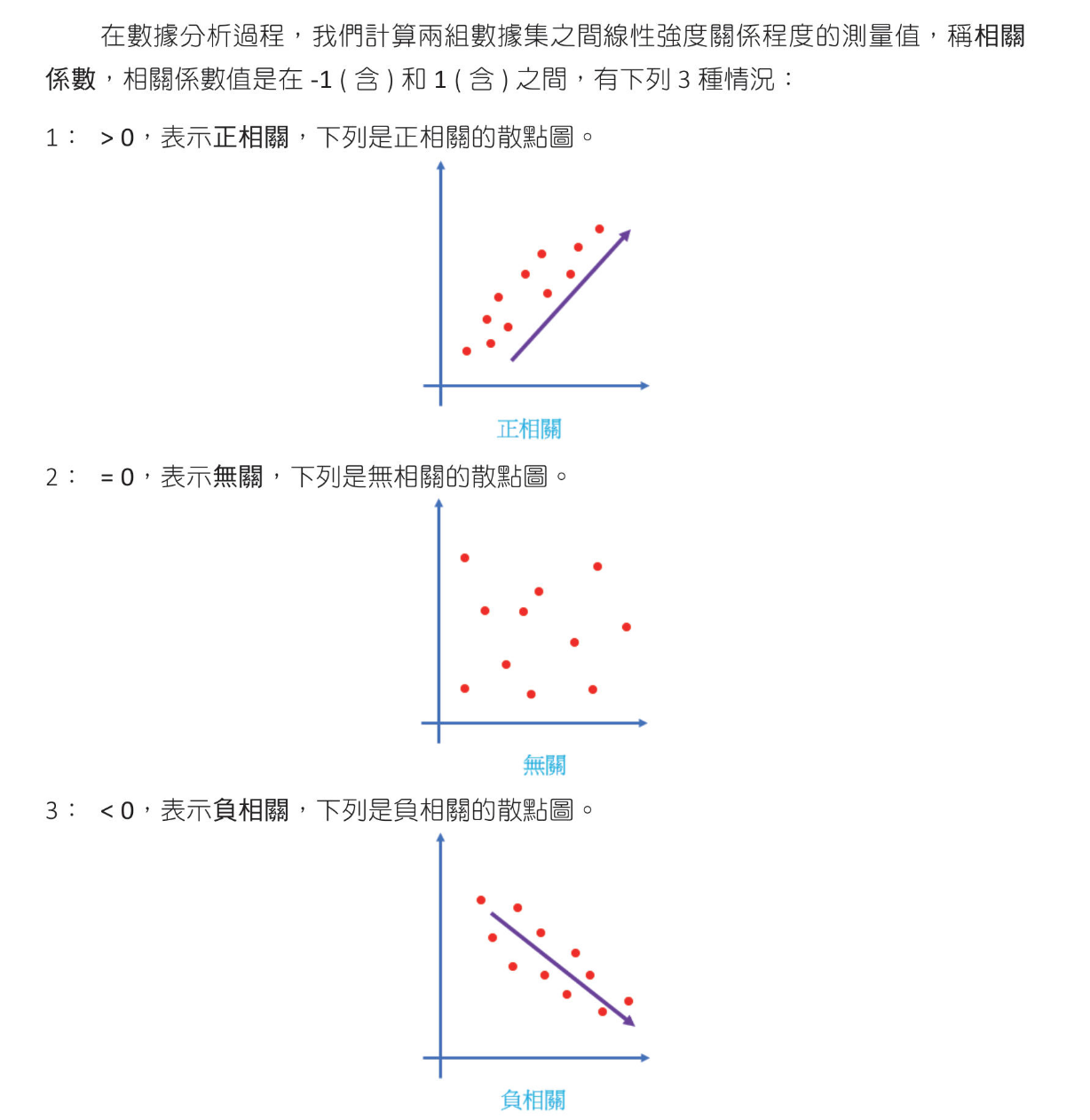
迴歸分析 相關係數(Correlation Coefficient) 相關係數絕對值小於0.3表低度相關,介於0.3和0.7表中度相關,大於0.7表高度相關
$$ r = \frac{ \sum_{i=1}^{n}(x_i-\overline{x})(y_y-\overline{x})}{\sqrt{\sum_{i=1}^{n}(x_i-\overline{x})^2}\sqrt{\sum_{i=1}^{n}(y_i-\overline{y})^2}} $$
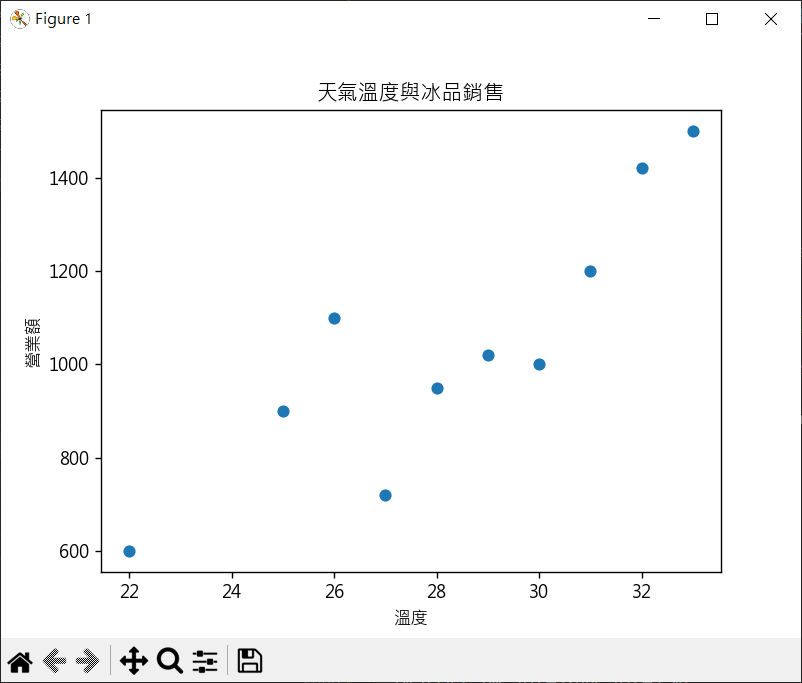
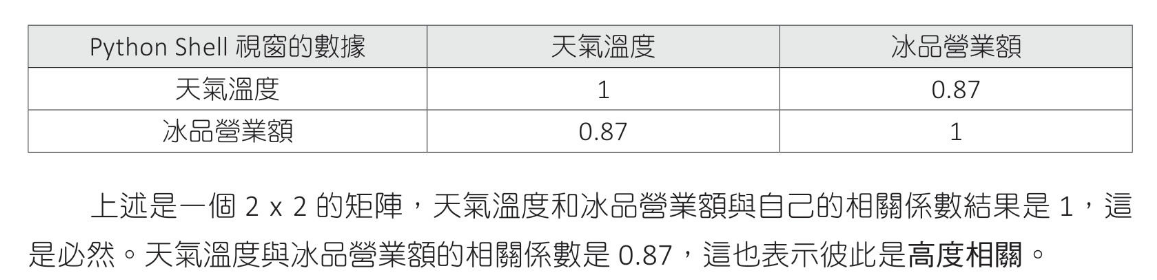
天氣溫度與冰品營業額新關係數計算
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 import matplotlib.pyplot as pltimport numpy as npplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] temperature = [25 ,31 ,28 ,22 ,27 ,30 ,29 ,33 ,32 ,26 ] rev = [900 ,1200 ,950 ,600 ,720 ,1000 ,1020 ,1500 ,1420 ,1100 ] print (f"相關係數 = {np.corrcoef(temperature, rev).round (2 )} " )plt.scatter(temperature, rev) plt.title("天氣溫度與冰品銷售" ) plt.xlabel("溫度" ) plt.ylabel("營業額" ) plt.show()
建立線性回歸模型與數據預測 建立迴歸模型係數 建立迴歸直線函數
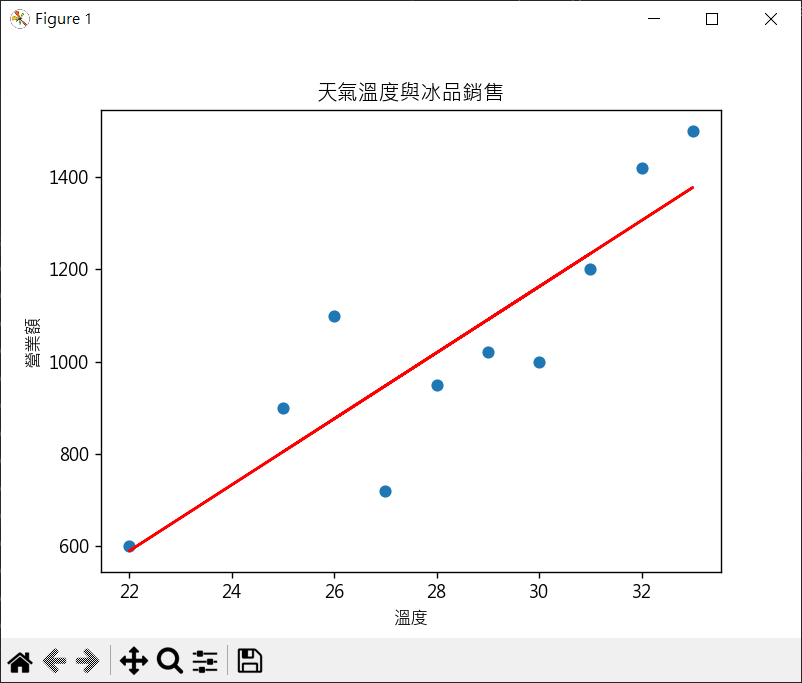
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 import matplotlib.pyplot as pltimport numpy as npplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] temperature = [25 ,31 ,28 ,22 ,27 ,30 ,29 ,33 ,32 ,26 ] rev = [900 ,1200 ,950 ,600 ,720 ,1000 ,1020 ,1500 ,1420 ,1100 ] coef = np.polyfit(temperature, rev, 1 ) reg = np.poly1d(coef) print (coef.round (2 ))print (reg)print (f"計算溫度 35 度時冰品銷售營業額 = {reg(35 ).round (0 )} " )plt.plot(temperature, reg(temperature) , color='red' ) plt.scatter(temperature, rev) plt.title("天氣溫度與冰品銷售" ) plt.xlabel("溫度" ) plt.ylabel("營業額" ) plt.show()
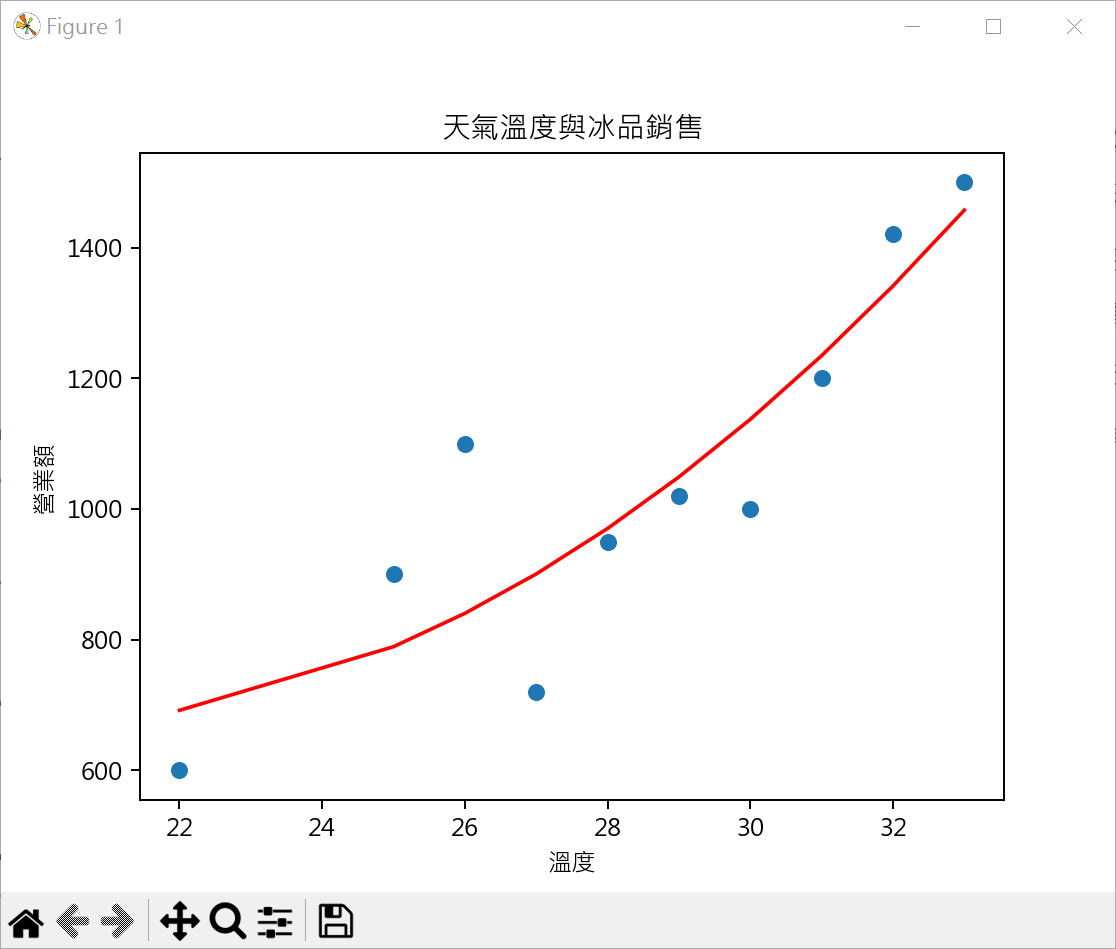
二次函數回歸模型 繪製二次函數圖形時,需先將數據依溫度排序,否則所繪製的迴歸圖形會有錯亂建立二次函數迴歸模型係數 建立二次函數迴歸方程式
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 import matplotlib.pyplot as pltimport numpy as npplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] temperature = [22 ,25 ,26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] rev = [600 ,900 ,1100 ,720 ,950 ,1020 ,1000 ,1200 ,1420 ,1500 ] coef = np.polyfit(temperature, rev, 2 ) reg = np.poly1d(coef) print (coef.round (2 ))print (reg)plt.plot(temperature, reg(temperature) , color='red' ) plt.scatter(temperature, rev) plt.title("天氣溫度與冰品銷售" ) plt.xlabel("溫度" ) plt.ylabel("營業額" ) plt.show()
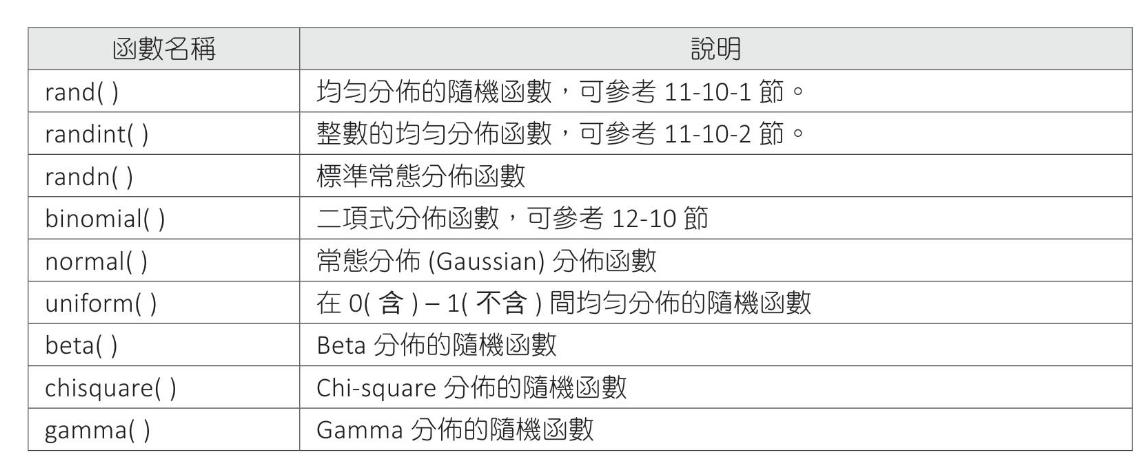
隨機函數的分布 常見Numpy的隨機函數
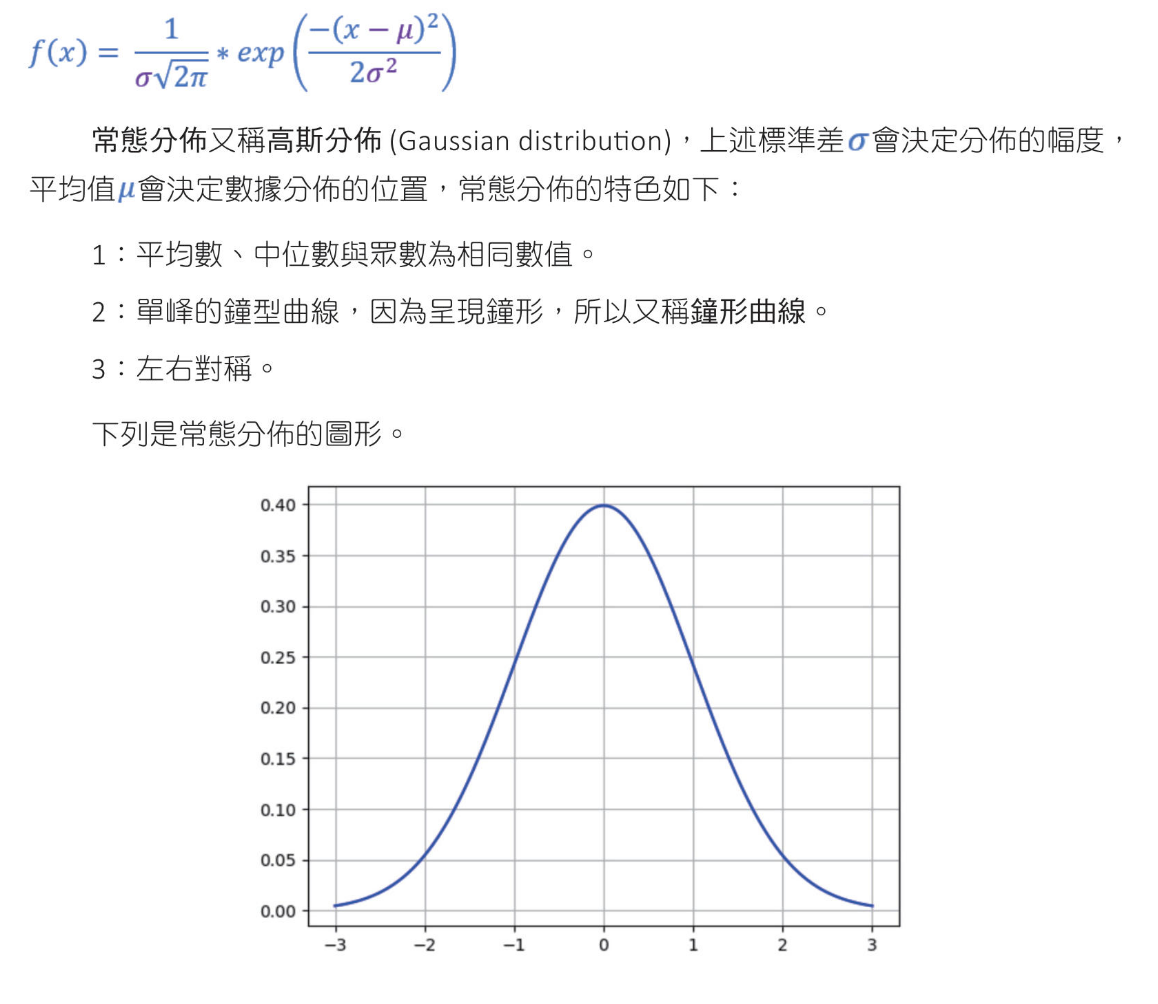
常態分布(normal distribution)函數的數學公式
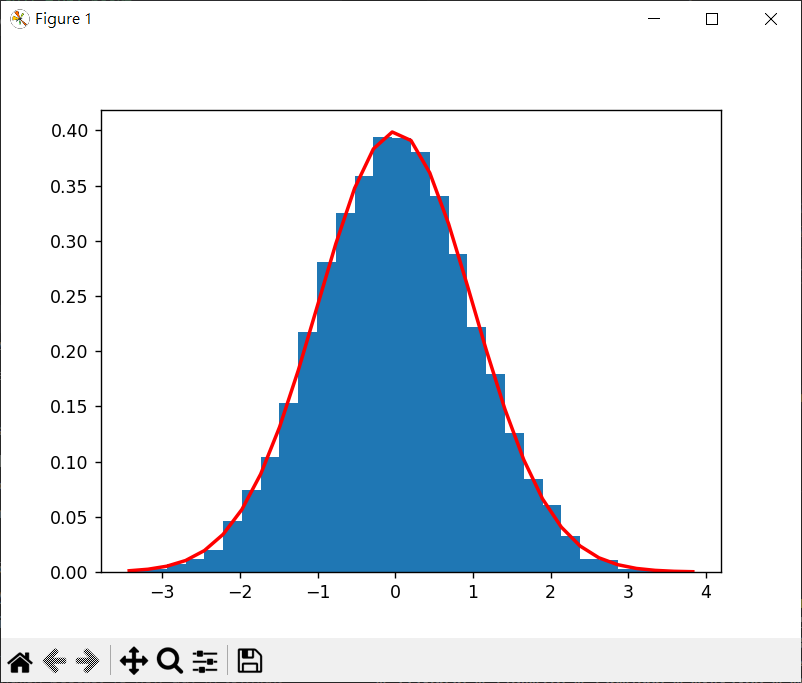
randn() 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 import matplotlib.pyplot as pltimport numpy as npmu = 0 sigma = 1 s = np.random.randn(10000 ) count, bins, ignored = plt.hist(s, 30 , density=True ) print (f"{len (count)} count={count} " )print (f"{len (bins)} ,bins={bins} " )print (f"ignored={ignored} " )plt.plot(bins, 1 /(sigma * np.sqrt( 2 * np.pi)) * np.exp( -(bins - mu)**2 / (2 *sigma**2 )) , linewidth=2 , color='r' ) plt.show()
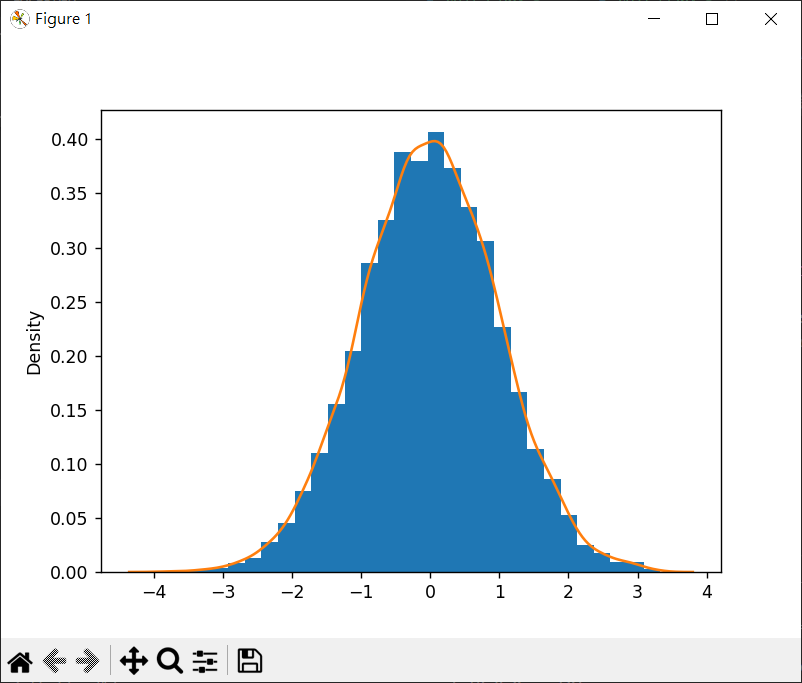
normal() 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 import matplotlib.pyplot as pltimport numpy as npimport seaborn as snsmu = 0 sigma = 1 s = np.random.normal(mu, sigma, 10000 ) count, bins, ignored = plt.hist(s, 30 , density=True ) sns.kdeplot(s) plt.show()
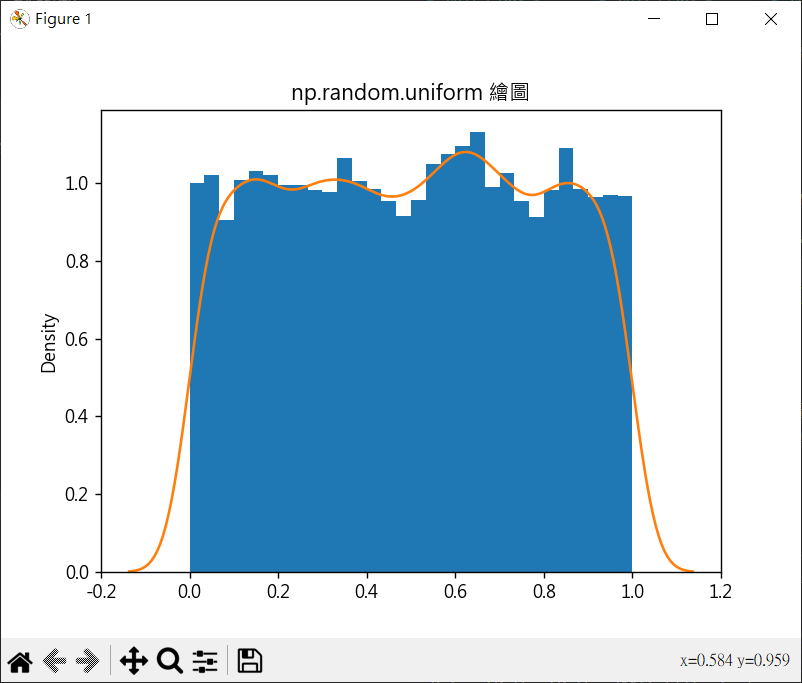
uniform(low, high, size) 平均分布的隨機函數
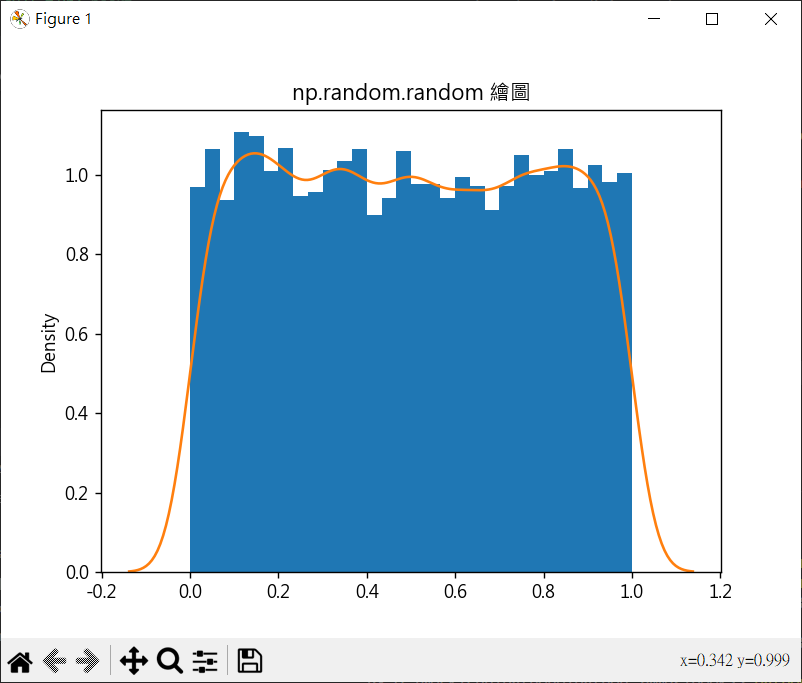
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import matplotlib.pyplot as pltimport numpy as npimport seaborn as snsplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False s = np.random.random(10000 ) plt.hist(s, 30 , density=True ) sns.kdeplot(s) plt.title("np.random.random 繪圖" ) plt.show()
向量 機器學習的向量知識
向量的長度 $|\mathbf{a}| or ||\mathbf{a}||$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 >>> import numpy as np >>> park = np.array([1,3]) >>> norm_park = np.linalg.norm(park) >>> norm_park 3.1622776601683795 >>> store = np.array([2, 1]) >>> office = np.array([4, 4]) >>> store_office = office - store >>> norm_store_office = np.linalg.norm(store_office) >>> norm_store_office 3.605551275463989
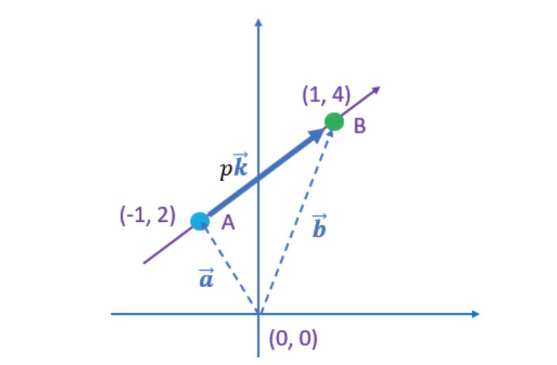
向量方程式
$\overrightarrow{a} = \left( ^{-1} _2\right)$
$\overrightarrow{k} = \left( ^{2} _2\right), p=1$
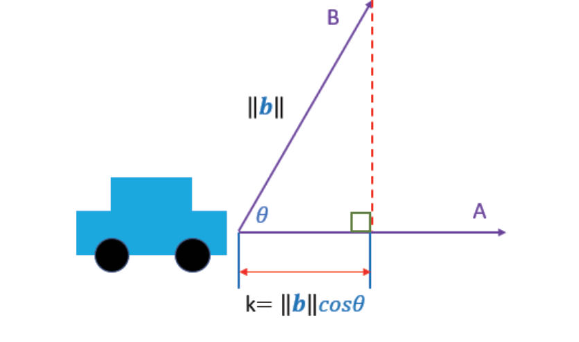
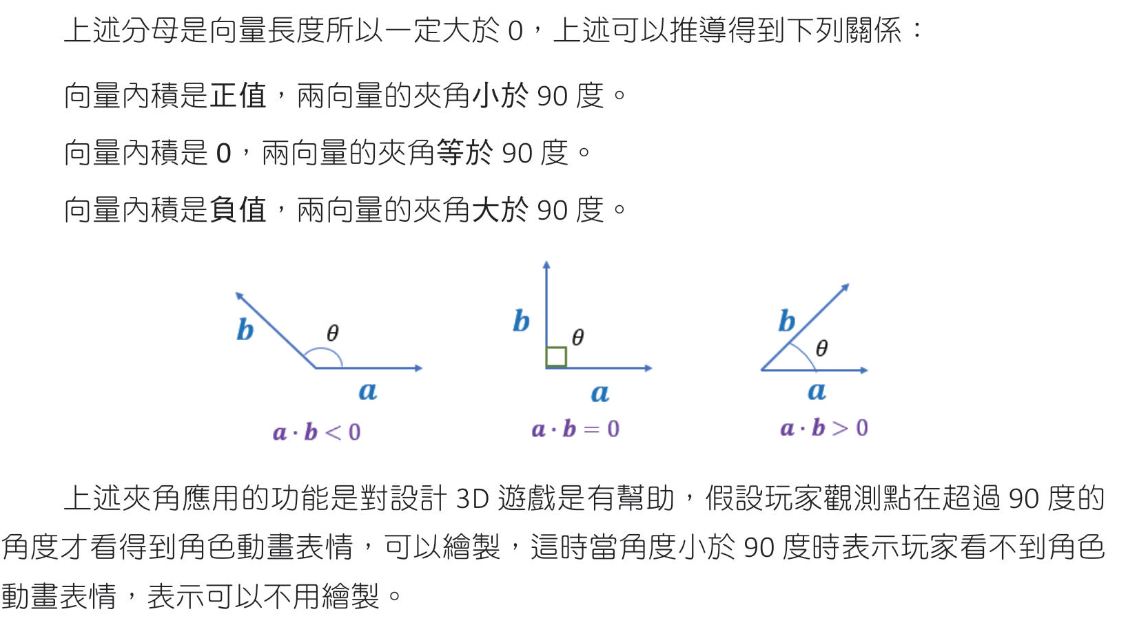
向量內積 偕同工作
$ k = \parallel{b}\parallel \cos{θ} $
1 2 3 >>> import math >>> 10*math.cos(math.radians(60)) 5.000000000000001
向量內積的定義 向量內積的幾何定義和代數定義是相同的,只是表達方式不同。具體來說,它們是兩個等價的定義,描述了同一個運算。
向量內積(inner product) a⋅b (a dot b)
幾何定義向量內積 $a⋅b = \parallel{a}\parallel \parallel{b}\parallel \cos{θ} $
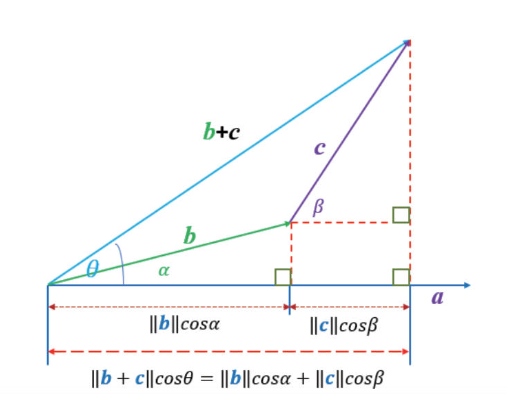
交換率
分配律
a⋅(b+c) = a⋅b + a⋅c
代數定義向量內積 $\mathbf{a} = (a_1 a_2 … a_n)$
1 2 3 4 5 6 >>> import numpy as np >>> a = np.array([1, 3]) >>> b = np.array([4, 2]) >>> np.dot(a, b) 10
幾何定義與代數定義是相等 幾何定義
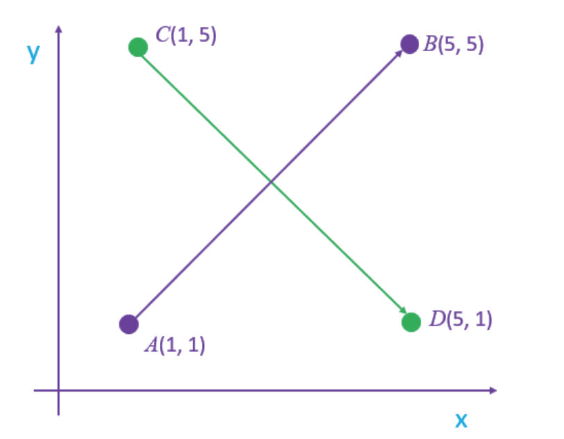
兩條直線的夾角 $a⋅b = \parallel{a}\parallel \parallel{b}\parallel \cos{θ} = a_1b_1 + a_2b_2$
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 import numpy as npimport matha = np.array([1 ,1 ]) b = np.array([5 ,5 ]) c = np.array([1 ,5 ]) d = np.array([5 ,1 ]) ab = b - a cd = d - c norm_ab = np.linalg.norm(ab) norm_cd = np.linalg.norm(cd) dot_ab_cd = np.dot(ab, cd) cos_value = dot_ab_cd/(norm_ab * norm_cd) cos_value = dot_ab_cd/(norm_ab * norm_cd) rad = math.acos(cos_value) deg = math.degrees(rad) print (f"角度是:{deg} " )
向量內積的性質 $ \cos{θ} = \frac{a_1b_1 + a_2b_2}{\parallel{a}\parallel \parallel{b}\parallel} $
餘弦相似度 $ 弦相似度(consine similarity) = \cos{θ} = \frac{a_1b_1 + a_2b_2}{\parallel{a}\parallel \parallel{b}\parallel} $
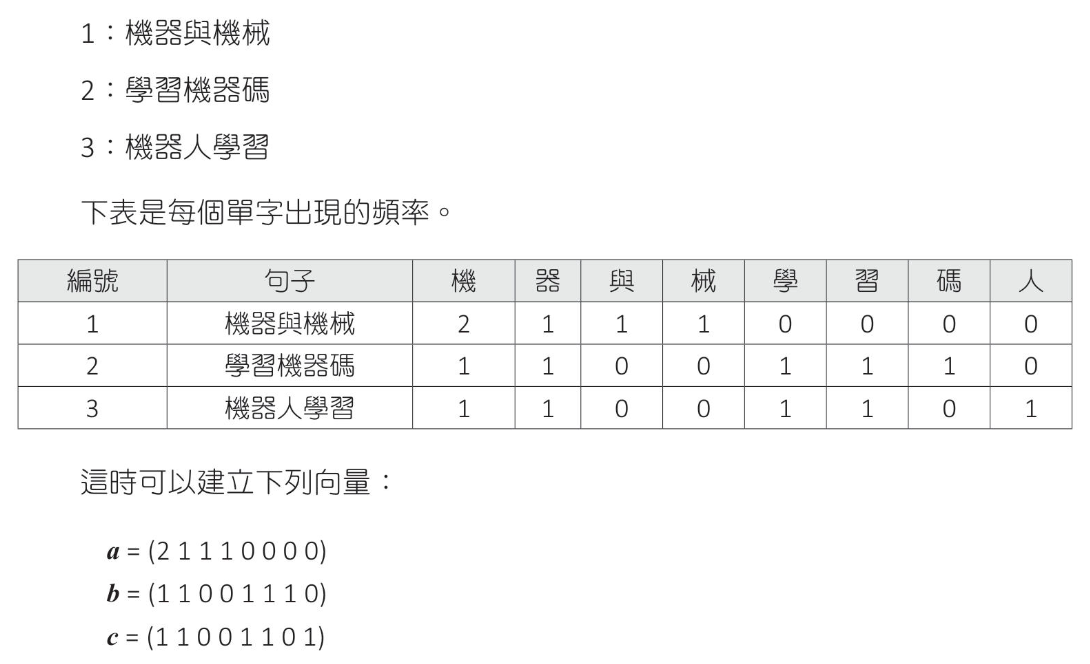
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import numpy as npdef consine_similarity (va, vb ): norm_a = np.linalg.norm(va) norm_b = np.linalg.norm(vb) dot_ab = np.dot(va, vb) return dot_ab/(norm_a * norm_b ) a = np.array([2 , 1 , 1 , 1 , 0 , 0 , 0 , 0 ]) b = np.array([1 , 1 , 0 , 0 , 1 , 1 , 1 , 0 ]) c = np.array([1 , 1 , 0 , 0 , 1 , 1 , 0 , 1 ]) print (f" a 和 b 的相似度 : {consine_similarity(a, b)} " )print (f" a 和 c 的相似度 : {consine_similarity(a, c)} " )print (f" b 和 c 的相似度 : {consine_similarity(b, c)} " )
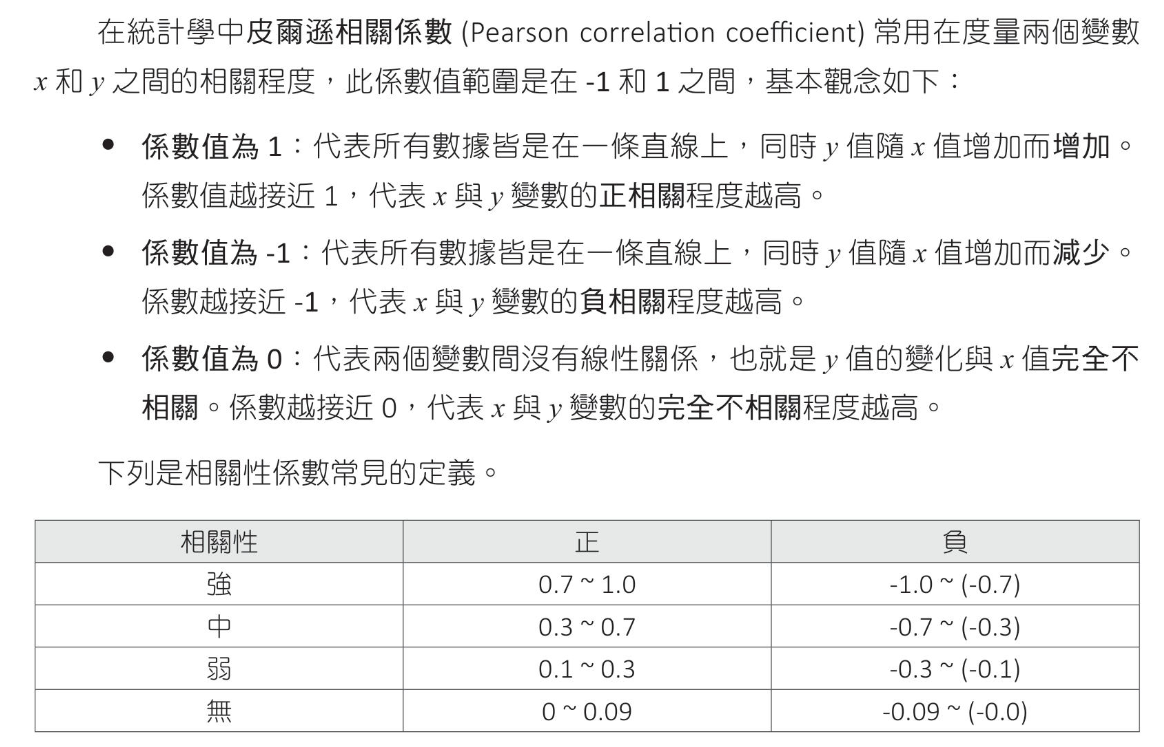
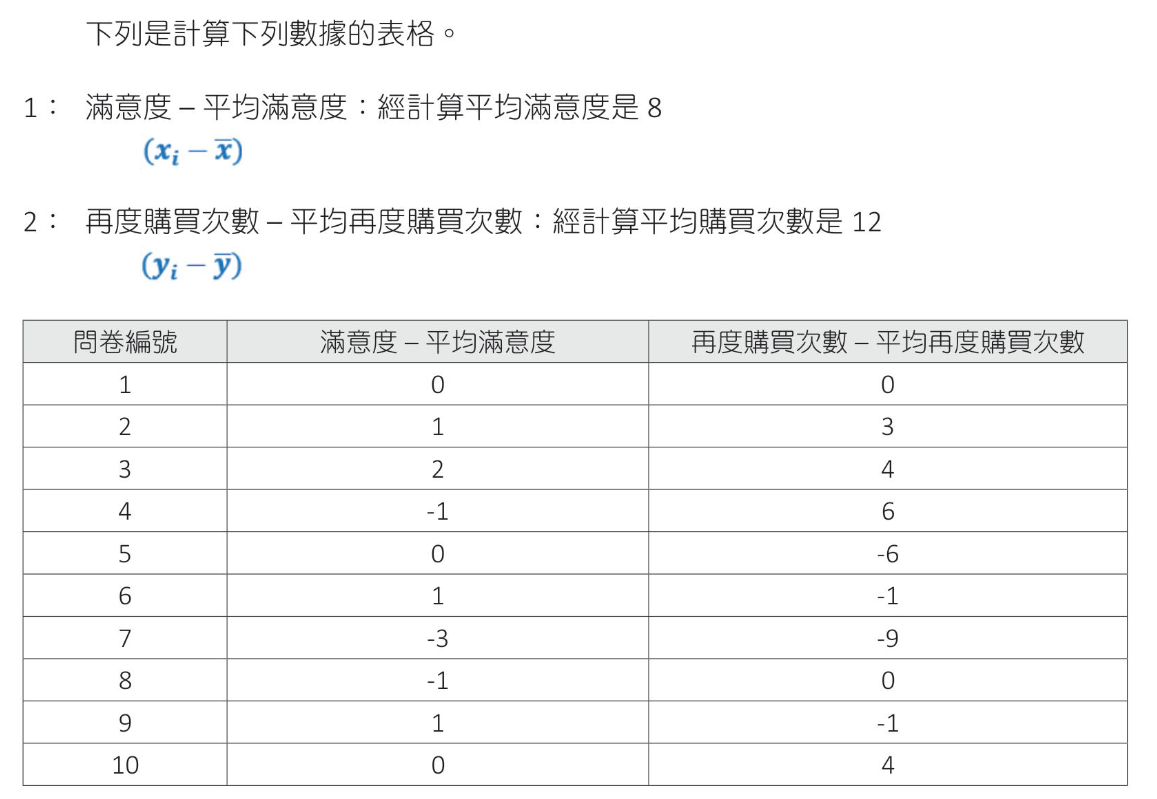
皮爾遜相關係數(Pearson correlation coefiicient)
皮爾遜相關係數定義 皮爾遜相關係數定義是兩個變數之間共變異數和標準差的商
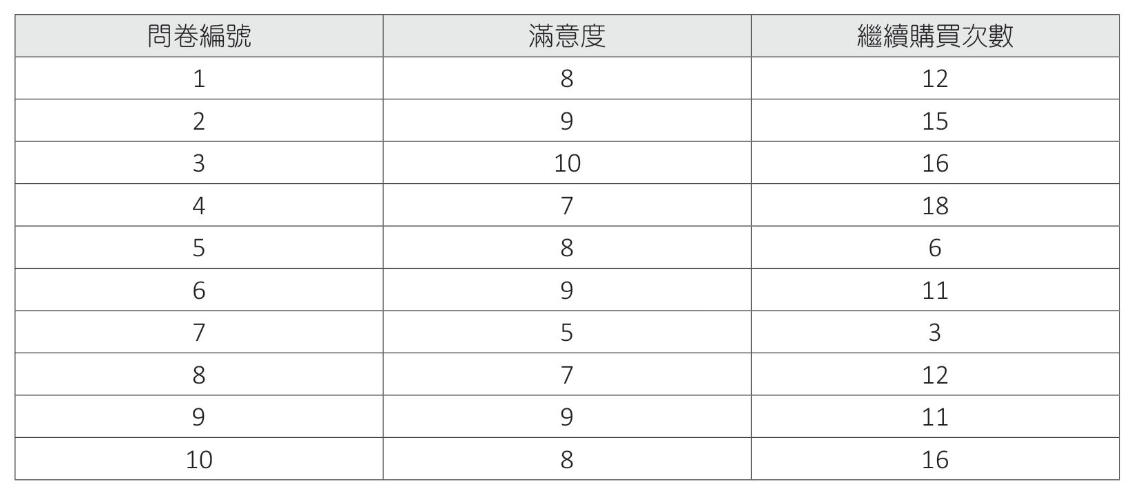
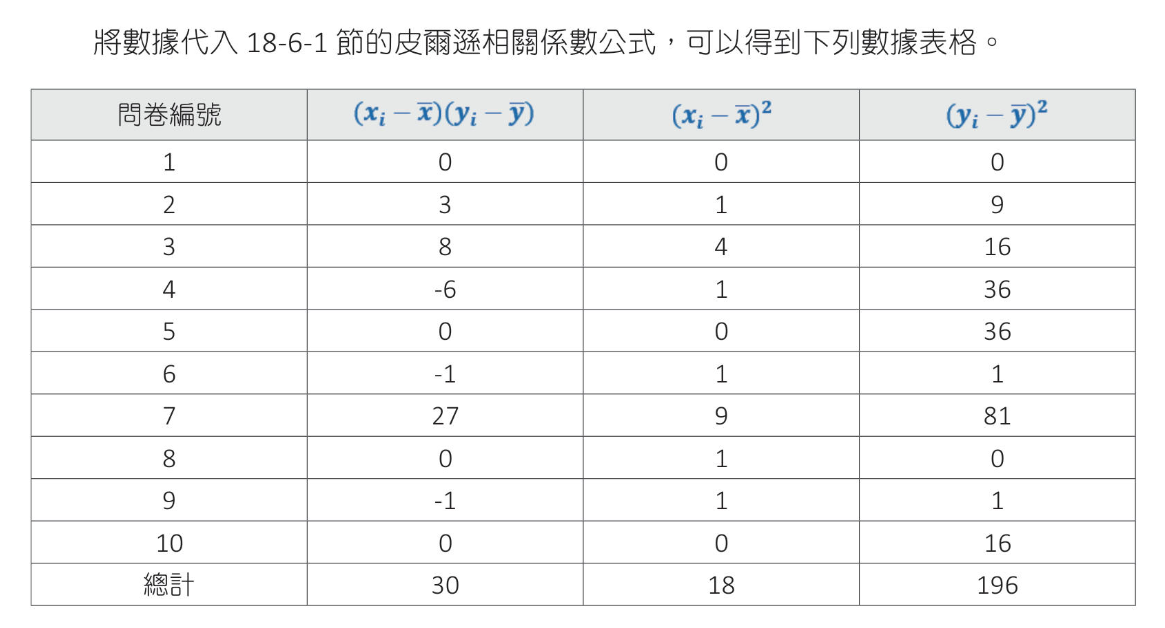
網路購物問卷調查案例解說 2019年12月做問卷調查,2021年1月再對詢問對象調查商品繼續購買次數
$ r = \frac{30}{\sqrt{18}\sqrt{196}} = 0.505$
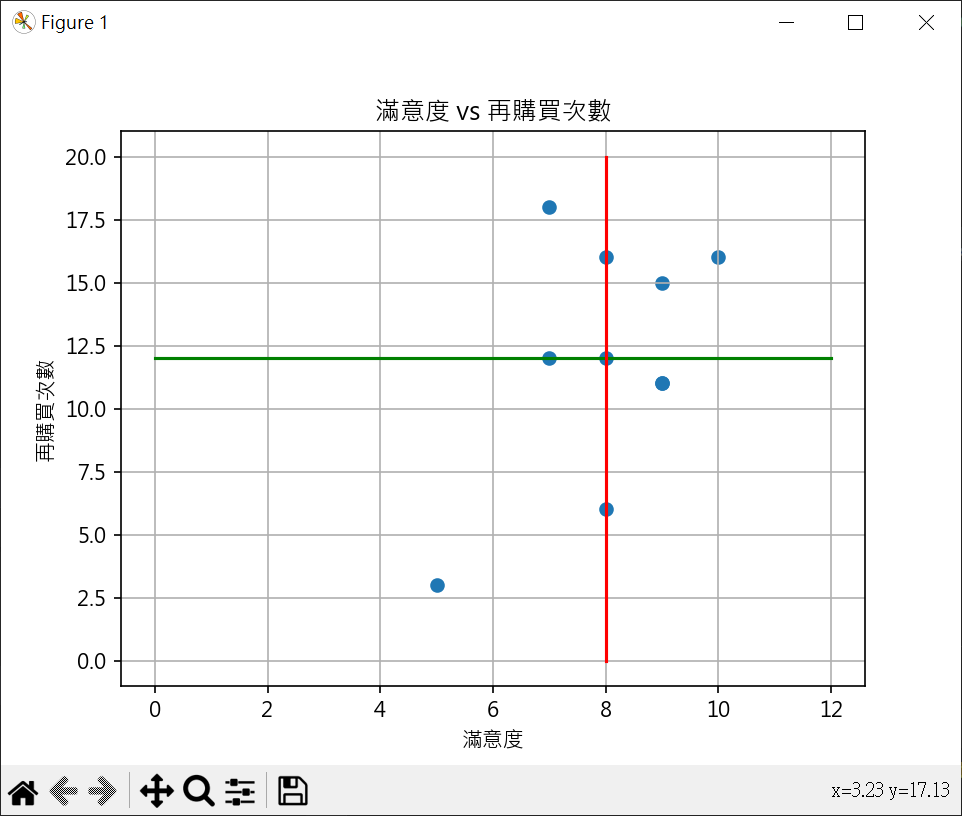
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 import numpy as npimport matplotlib.pyplot as pltx = np.array([8 ,9 ,10 ,7 ,8 ,9 ,5 ,7 ,9 ,8 ]) y = np.array([12 ,15 ,16 ,18 ,6 ,11 ,3 ,12 ,11 ,16 ]) x_mean = np.mean(x) y_mean = np.mean(y) xi_x =[v - x_mean for v in x] yi_x =[v - y_mean for v in y] data1 = [0 ] * 10 data2 = [0 ] * 10 data3 = [0 ] * 10 for i in range (len (x)): data1[i] = xi_x[i] * yi_x[i] data2[i] = xi_x[i]**2 data3[i] = yi_x[i]**2 v1 = np.sum (data1) v2 = np.sum (data2) v3 = np.sum (data3) r = v1/((v2**0.5 )*(v3**0.5 )) print (f"coefficient={r:.3 f} " )plt.rcParams["font.family" ] = ["Microsoft JhengHei" ] xpt1 = np.linspace(0 , 12 , 12 ) ypt1 = [y_mean for xp in xpt1] ypt2 = np.linspace(0 , 20 , 20 ) xpt2 = [x_mean for xp in ypt2] plt.scatter(x, y) plt.plot(xpt1, ypt1, color="g" ) plt.plot(xpt2, ypt2, color="r" ) plt.title("滿意度 vs 再購買次數" ) plt.xlabel("滿意度" ) plt.ylabel("再購買次數" ) plt.grid() plt.show()
使用向量內積計算係數 $a = (x_1-\overline{x}\ x_2-\overline{x} … x_n-\overline{x}) $
分子
分母
推導結果
向量外積
向量外積的定義如下:假設我們有兩個向量 𝑎 和 𝑏
$ b =
$ c = a × b =
公式
$a × b = \begin{vmatrix} i & j & k \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{vmatrix} = \begin{pmatrix} a_yb_z - a_zb_y \\ a_zb_x - a_xb_z \\ a_xb_y - a_yb_x \end{pmatrix}$
例子
$ a × b = \begin{vmatrix} i & j & k \\ 1 & 2 & 3 \\ 4 & 5 & 6 \end{vmatrix} = \begin{pmatrix} 2⋅6 - 3⋅5 \\ 3⋅4 − 1⋅6 \\ 1⋅5 − 2⋅4 \end{pmatrix} = \begin{pmatrix} 12 - 15 \\ 12 − 6 \\ 5 − 8 \end{pmatrix} = \begin{pmatrix} -3 \\ 6 \\ -3 \end{pmatrix} $
1 2 3 4 5 >>> import numpy as np>>> a = np.array([1 , 2 , 3 ])>>> b = np.array([4 , 5 , 6 ])>>> np.cross(a, b)array([-3 , 6 , -3 ])
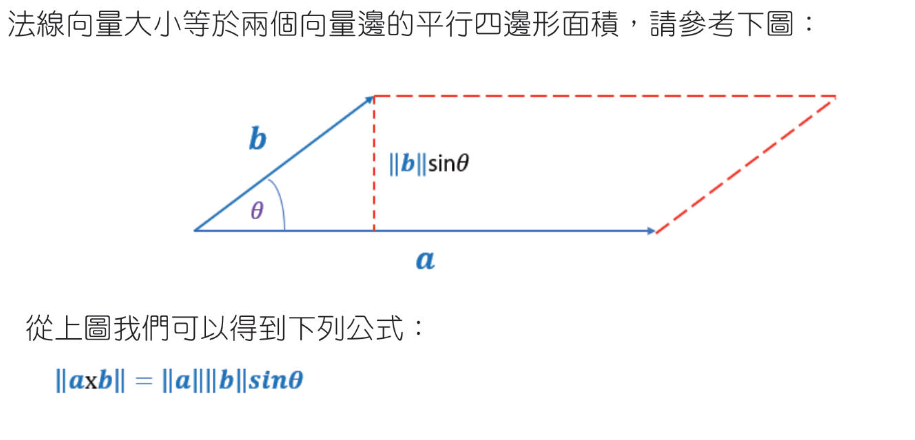
計算面積
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 import numpy as npimport matha = np.array([4 , 2 ]) b = np.array([1 , 3 ]) norm_a = np.linalg.norm(a) norm_b = np.linalg.norm(b) dot_ab = np.dot(a, b) cos_value = dot_ab/(norm_a*norm_b) rad = math.acos(cos_value) area = norm_a * norm_b * math.sin(rad)/2 print (f"計算角度再算面積 area={area:.2 f} " )ab_cross = np.cross(a,b) area2 = ab_cross / 2 print (f"以外積計算面積 area={area2:.2 f} " )
矩陣 矩陣表達方式 矩陣的行與列 2*3矩陣
其他表示法 $ \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix} $
矩陣相加與相減 矩陣大小要一樣直接相加減
1 2 3 4 5 6 7 8 9 10 import numpy as npA = np.matrix([[1 ,2 ,3 ], [4 ,5 ,6 ]]) B = np.matrix([[4 ,5 ,6 ], [7 ,8 ,9 ]]) print (f"A + B = {A + B} " )print (f"A - B = {A - B} " )
矩陣相乘 A * B, A矩陣的行數要等於 B矩陣的列數
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import numpy as npA = np.matrix([[1 ,2 ], [3 , 4 ]]) B = np.matrix([[5 ,6 ], [7 ,8 ]]) print (f"A * B = {A * B} " )C = np.matrix([[ 1 , 0 , 2 ], [-1 , 3 , 1 ]]) D = np.matrix([[3 ,1 ], [2 ,1 ], [1 ,0 ]]) print (f"C * D = {C * D} " )
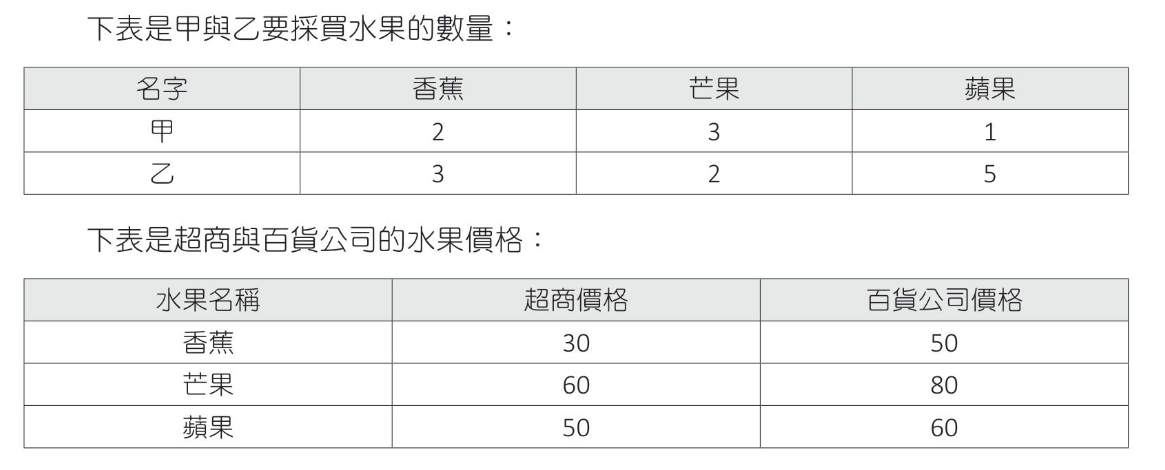
計算甲和乙在超商及百貨公司採買各需多少錢
1 2 3 4 5 6 7 8 9 10 11 import numpy as npA = np.matrix([[2 , 3 , 1 ], [3 , 2 , 5 ]]) B = np.matrix([[30 , 50 ], [60 , 80 ], [50 , 60 ]]) print (f"A * B = {A * B} " )
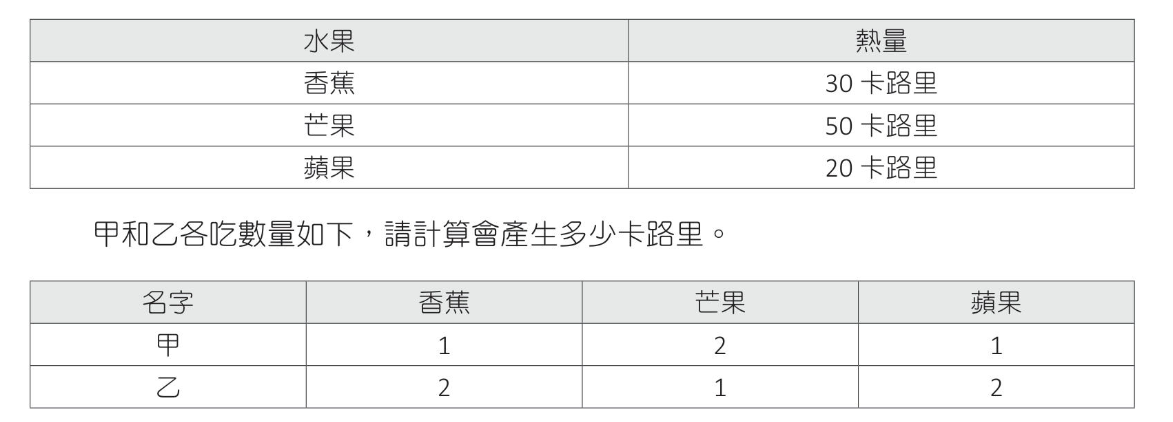
計算甲,乙各吃下多少熱量
1 2 3 4 5 6 7 8 9 import numpy as npA = np.matrix([[1 , 2 , 1 ], [2 , 1 , 2 ]]) B = np.matrix([[30 ],[50 ],[20 ]]) print (f"A * B = {A * B} " )
方形矩陣(square matrix) 一個矩陣列數等於行數
單位矩陣(indentity matrix) 一個方形矩陣由左上至右下對角線的元素為1,其他元素為0
1 2 3 4 5 6 7 8 9 10 11 12 import numpy as npA = np.matrix([[1 , 2 ], [3 , 4 ]]) B = np.matrix([[1 , 0 ], [0 , 1 ]]) print (f"A * B = {A * B} " )print (f"B * A = {B * A} " )
反矩陣(inverse matrix) 只有方矩陣才有反矩陣,一個矩陣乘以反矩陣可以得到E,A的反矩陣表示為$A^{-1}$
2*2 反矩陣公式如下
反矩陣實例
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 import numpy as npA = np.matrix([[2 , 3 ], [5 , 7 ]]) B = np.linalg.inv(A) product_1 = A * B product_2 = B * A print (f"A_inv = {B} " )print (f"A * A_inv = {product_1} " )print (f"A_inv * A = {product_2} " )print (f"A * A_inv(round) = {product_1.round ()} " )print (f"A_inv * A(round) = {product_2.round ()} " )
用反矩陣解聯立方程式 3x + 2y = 5
$ \begin{pmatrix} 3 & 2 \\ 1 & 2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 5 \\ -1 \end{pmatrix} $
$ \begin{pmatrix} 3 & 2 \\ 1 & 2 \end{pmatrix} 的反矩陣為 \begin{pmatrix} 0.5 & -0.5 \\ -2.5 & 0.75 \end{pmatrix}$
$ \begin{pmatrix} 0.5 & -0.5 \\ -2.5 & 0.75 \end{pmatrix} \begin{pmatrix} 3 & 2 \\ 1 & 2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0.5 & -0.5 \\ -2.5 & 0.75 \end{pmatrix} \begin{pmatrix} 5 \\ -1 \end{pmatrix} $
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 import numpy as npA = np.matrix([[3 , 2 ], [1 , 2 ]]) B = np.linalg.inv(A) C = np.matrix([[5 ], [-1 ]]) print (f"反矩陣 : {B} " )print (f"E : {B*A} " )print (f"解方程式 : {B*C} " )
張量(Tensor) 張量就是數據的結構,shape()可列出數字的外型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 import numpy as npA = np.array([ [[1 ,2 ], [3 ,4 ]], [[5 ,6 ], [7 ,8 ]], [[9 ,10 ], [11 ,12 ]], ]) print (f"A={A} " )print (f"shape = {np.shape(A)} " )
轉置矩陣 就是將矩陣內的列元素和行元素對調
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 import numpy as npA = np.array([[0 , 2 , 4 , 6 ], [1 , 3 , 5 , 7 ]]) B = A.T print (f"轉置矩陣1 = {B} " )C = np.transpose(A) print (f"轉置矩陣2 = {C} " )
轉置矩陣的應用 皮爾遜相關係數
$ a = \begin{pmatrix} x_1 - \overline{x} \\ x_2 - \overline{x} \\ … \\ x_n - \overline{x} \end{pmatrix} b = \begin{pmatrix} y_1 - \overline{y} \\ y_2 - \overline{y} \\ … \\ y_n - \overline{y} \end{pmatrix}$
$ a^T⋅b = \begin{pmatrix} x_1 - \overline{x} \\ x_2 - \overline{x} \\ … \\ x_n - \overline{x} \end{pmatrix} \begin{pmatrix} y_1 - \overline{y} \\ y_2 - \overline{y} \\ … \\ y_n - \overline{y} \end{pmatrix} $
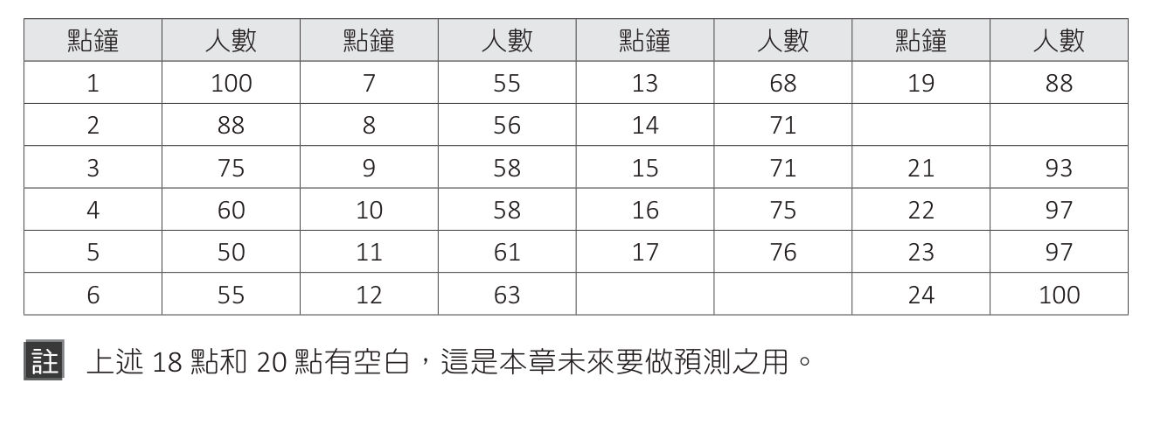
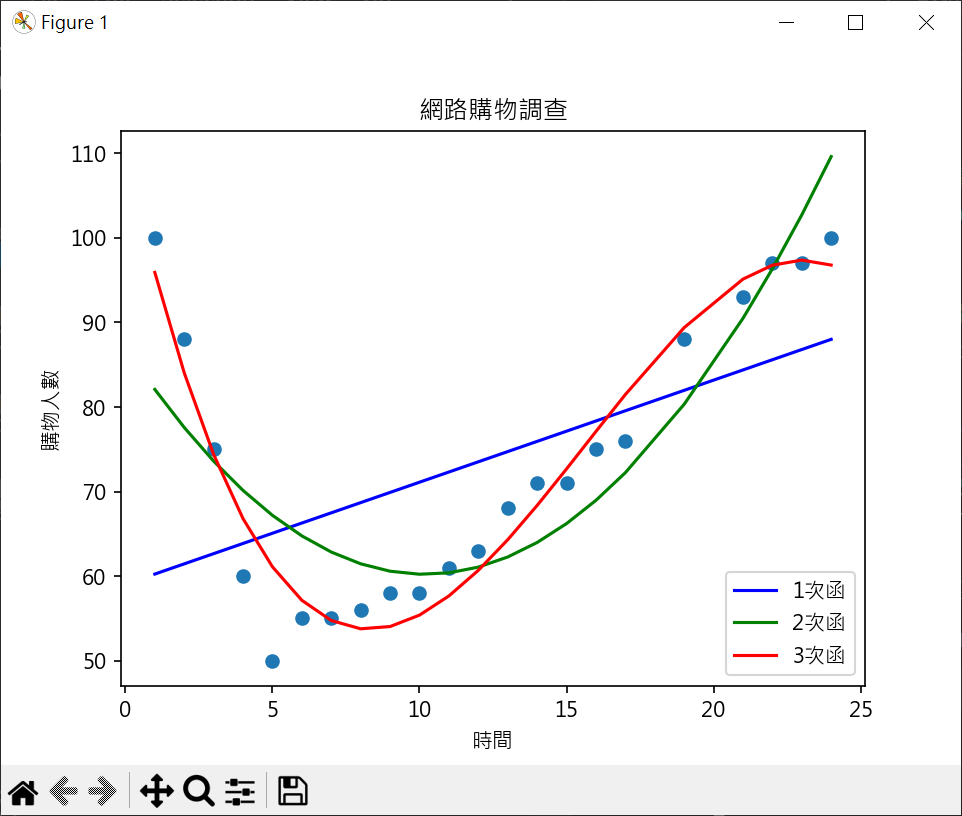
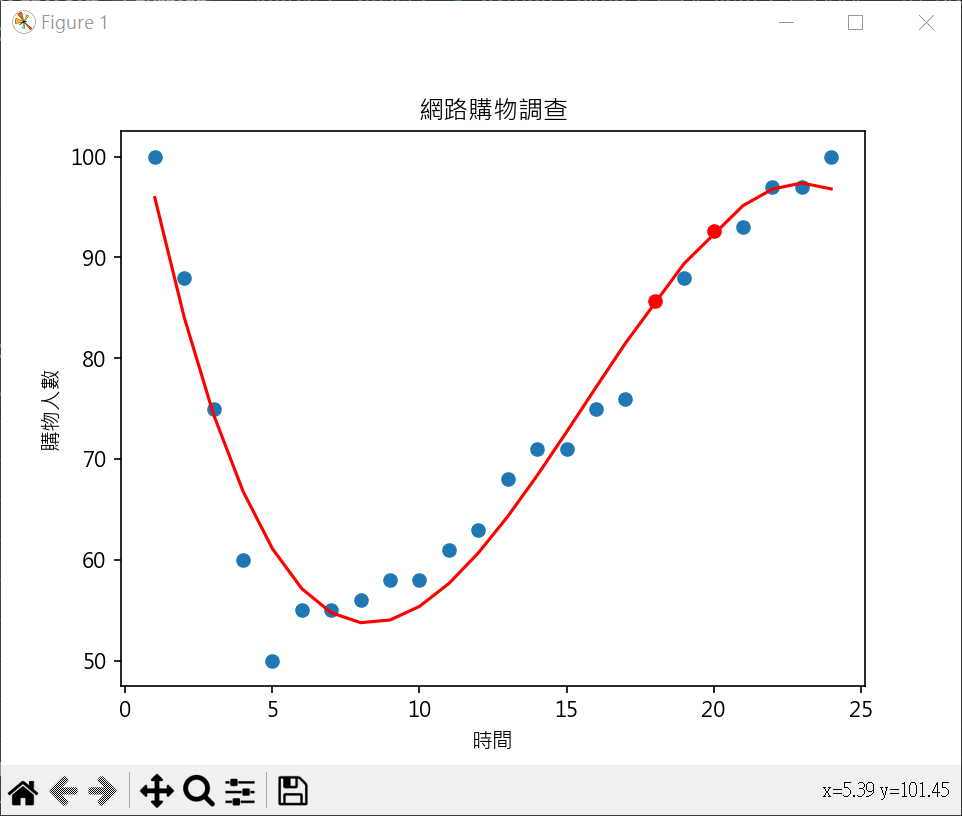
向量,矩陣與多元線性迴歸(20):不了解 三次函數迴歸曲線實作 網購迴歸曲線繪製
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 import matplotlib.pyplot as pltimport numpy as npplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] x = [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 ,10 ,11 , 12 ,13 ,14 ,15 ,16 ,17 ,19 ,21 ,22 ,23 ,24 ] y = [100 , 88 , 75 , 60 , 50 , 55 , 55 , 56 , 58 , 58 , 61 , 63 , 68 , 71 , 71 , 75 , 76 , 88 , 93 , 97 , 97 , 100 ] coef1 = np.polyfit(x, y, 1 ) model1 = np.poly1d(coef1) coef2 = np.polyfit(x, y, 2 ) model2 = np.poly1d(coef2) coef3 = np.polyfit(x, y, 3 ) model3 = np.poly1d(coef3) print (model1)print (model2)print (model3)plt.plot(x, model1(x) , color='blue' , label="1次函" ) plt.plot(x, model2(x) , color='green' , label="2次函" ) plt.plot(x, model3(x) , color='red' , label="3次函" ) plt.scatter(x, y ) plt.title("網路購物調查" ) plt.xlabel("時間" ) plt.ylabel("購物人數" ) plt.legend() plt.show()
使用 scikit-learn 評估迴歸模型 # 評估模型
預測未來值 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 import matplotlib.pyplot as pltimport numpy as npplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] x = [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 ,10 ,11 , 12 ,13 ,14 ,15 ,16 ,17 ,19 ,21 ,22 ,23 ,24 ] y = [100 , 88 , 75 , 60 , 50 , 55 , 55 , 56 , 58 , 58 , 61 , 63 , 68 , 71 , 71 , 75 , 76 , 88 , 93 , 97 , 97 , 100 ] coef = np.polyfit(x, y, 3 ) model = np.poly1d(coef) print (f"18點購物人數預測 : {model(18 ):.2 f} " )print (f"20點購物人數預測 : {model(20 ):.2 f} " )plt.plot(18 , model(18 ), "-o" , color="red" ) plt.plot(20 , model(20 ), "-o" , color="red" ) plt.plot(x, model(x) , color='red' ) plt.scatter(x, y ) plt.title("網路購物調查" ) plt.xlabel("時間" ) plt.ylabel("購物人數" ) plt.show()
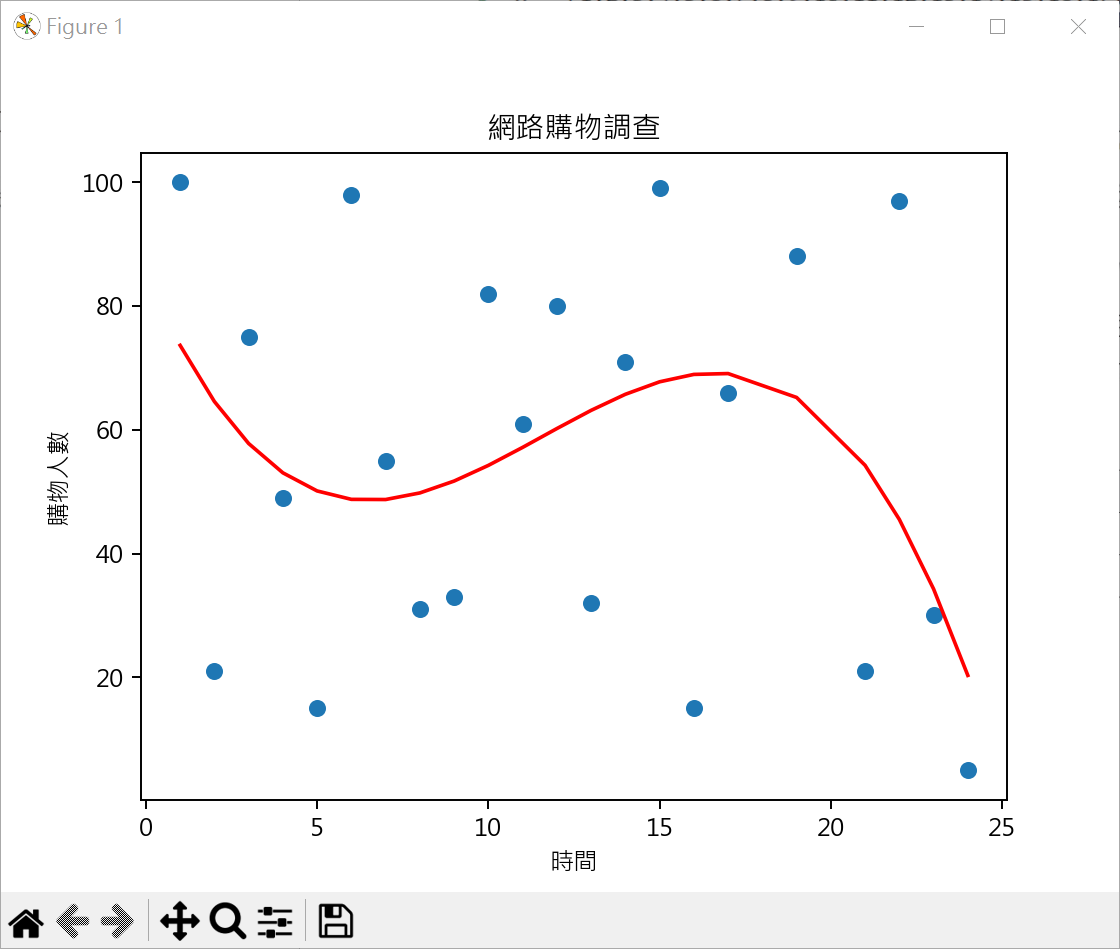
不適合三次函數迴歸數據(實例) 不是所有數據皆可使用三次函數求迴歸模型
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 from sklearn.metrics import r2_score, mean_squared_errorimport matplotlib.pyplot as pltimport numpy as npplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] x = [ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 ,10 ,11 , 12 ,13 ,14 ,15 ,16 ,17 ,19 ,21 ,22 ,23 ,24 ] y = [100 , 21 , 75 , 49 , 15 , 98 , 55 , 31 , 33 , 82 , 61 , 80 , 32 , 71 , 99 , 15 , 66 , 88 , 21 , 97 , 30 , 5 ] coef = np.polyfit(x, y, 3 ) model = np.poly1d(coef) print (f"MSE:{mean_squared_error(y, model(x)):.3 f} " )print (f"R2_Score:{r2_score(y, model(x)):.3 f} " )plt.plot(x, model(x) , color='red' ) plt.scatter(x, y ) plt.title("網路購物調查" ) plt.xlabel("時間" ) plt.ylabel("購物人數" ) plt.show()
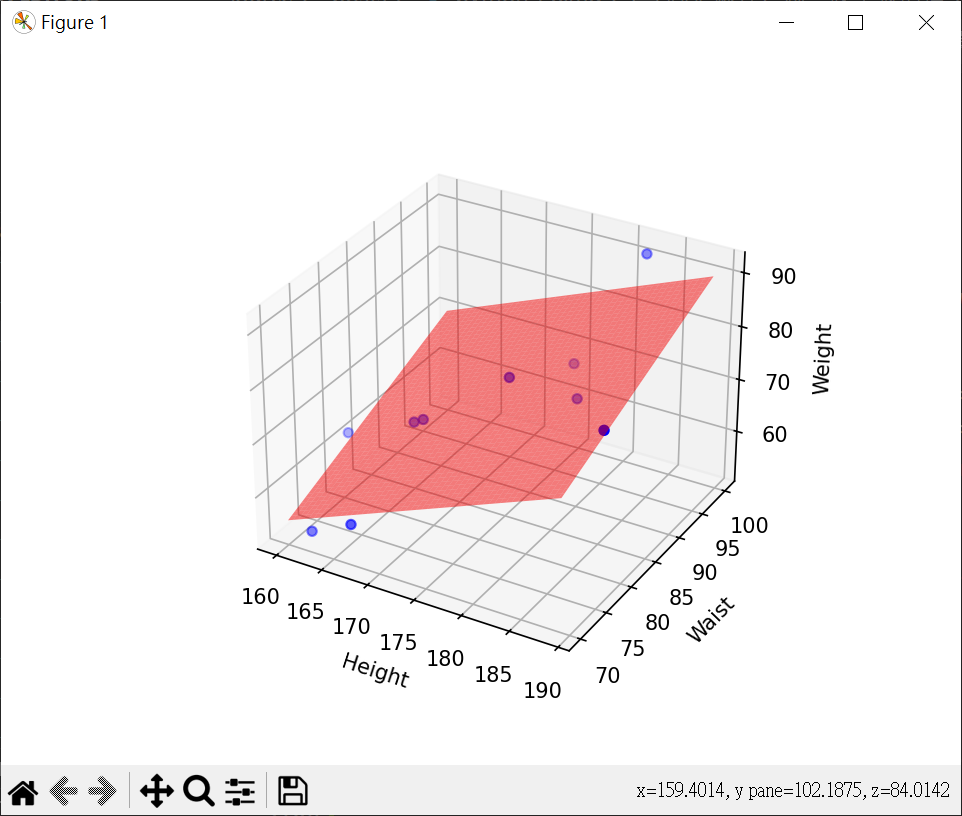
線性迴歸 - 波士頓房價 簡單資料測試 產生迴歸模型(身高.腰圍與體重的測試)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 import pandas as pdimport numpy as npfrom sklearn.linear_model import LinearRegressionimport matplotlib.pyplot as pltdata = { 'height' : [162 , 160 , 167 , 180 , 177 , 168 , 189 , 182 , 176 , 169 ], 'waist' : [ 71 , 81 , 70 , 90 , 95 , 80 , 78 , 100 , 84 , 80 ], 'weight' : [ 53 , 62 , 58 , 71 , 72 , 69 , 80 , 91 , 78 , 70 ], } df = pd.DataFrame(data) X = df[['height' , 'waist' ]] y = df['weight' ] model = LinearRegression() model.fit(X, y) intercept = model.intercept_ coefficients = model.coef_ print (f"y截距(b0) : {intercept:.3 f} " )print (f"斜率(b1,b2): {coefficients.round (3 )} " )formula = f"y = {intercept:.3 f} " for i, coef in enumerate (coefficients): formula += f" + ({coef:.3 f} )*x{i+1 } " print ("線性迴歸方程式:" )print (formula)h = eval (input ("請輸入身高:" )) w = eval (input ("請輸入腰圍:" )) new_weight = pd.DataFrame(np.array([[h,w]]), columns=["height" , "waist" ]) print (new_weight)predicted = model.predict(new_weight) print (f"預測體重:{predicted[0 ]:.2 f} " )fig = plt.figure() ax = fig.add_subplot(111 , projection='3d' ) ax.scatter(df['height' ], df['waist' ], df['weight' ], color='blue' ) x_surf, y_surf = np.meshgrid(np.linspace(df['height' ].min (), df['height' ].max (), 100 ), np.linspace(df['waist' ].min (), df['waist' ].max (), 100 )) z_surf = intercept + coefficients[0 ] * x_surf + coefficients[1 ] * y_surf ax.plot_surface(x_surf, y_surf, z_surf, color='red' , alpha=0.5 ) ax.set_xlabel('Height' ) ax.set_ylabel('Waist' ) ax.set_zlabel('Weight' ) plt.show()
了解模型的優劣(R 平方係數) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 import pandas as pdfrom sklearn.linear_model import LinearRegressionfrom sklearn.model_selection import train_test_splitfrom sklearn.metrics import r2_scoredata = { 'height' : [162 , 160 , 167 , 180 , 177 , 168 , 189 , 182 , 176 , 169 ], 'waist' : [ 71 , 81 , 70 , 90 , 95 , 80 , 78 , 100 , 84 , 80 ], 'weight' : [ 53 , 62 , 58 , 71 , 72 , 69 , 80 , 91 , 78 , 70 ], } df = pd.DataFrame(data) X = df[['height' , 'waist' ]] y = df['weight' ] X_train, X_test, y_train, y_test = \ train_test_split(X, y, test_size=0.2 , random_state=1 ) model = LinearRegression() model.fit(X_train, y_train) intercept = model.intercept_ coefficients = model.coef_ print (f"y截距(b0) : {intercept:.3 f} " )print (f"斜率(b1,b2): {coefficients.round (3 )} " )formula = f"y = {intercept:.3 f} " for i, coef in enumerate (coefficients): formula += f" + ({coef:.3 f} )*x{i+1 } " print ("線性迴歸方程式:" )print (formula)y_pred = model.predict(X_test) print (f"R2_Score:{r2_score(y_test, y_pred):.2 f} " )
波士頓房價數據
列出資料數據 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 import pandas as pdboston = pd.read_csv("boston.csv" , sep='\s+' ) data = boston.iloc[:, :13 ] target = boston.iloc[:,13 :14 ] print (f"資料外型 : {boston.shape} " )print (f"自變數 樣品外型 : {data.shape} " )print (f"目標變數樣品外型 : {target.shape} " )print (data.head(3 ))print (target.head(3 ))print (f"{data.columns} " )print (f"{target.columns} " )
資料處理 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 import pandas as pdboston = pd.read_csv("boston.csv" , sep='\s+' ) data = boston.iloc[:, :13 ] target = boston.iloc[:,13 :14 ] pd.set_option('display.max_columns' , None ) pd.set_option('display.width' , 300 ) print (data.head())print (boston.head())print (boston.isnull().sum ())print (boston.corr())print (boston.corr().abs ().nlargest(3 , 'MEDV' ).index)print (boston.corr().abs ().nlargest(3 , 'MEDV' ).values[:,13 ])
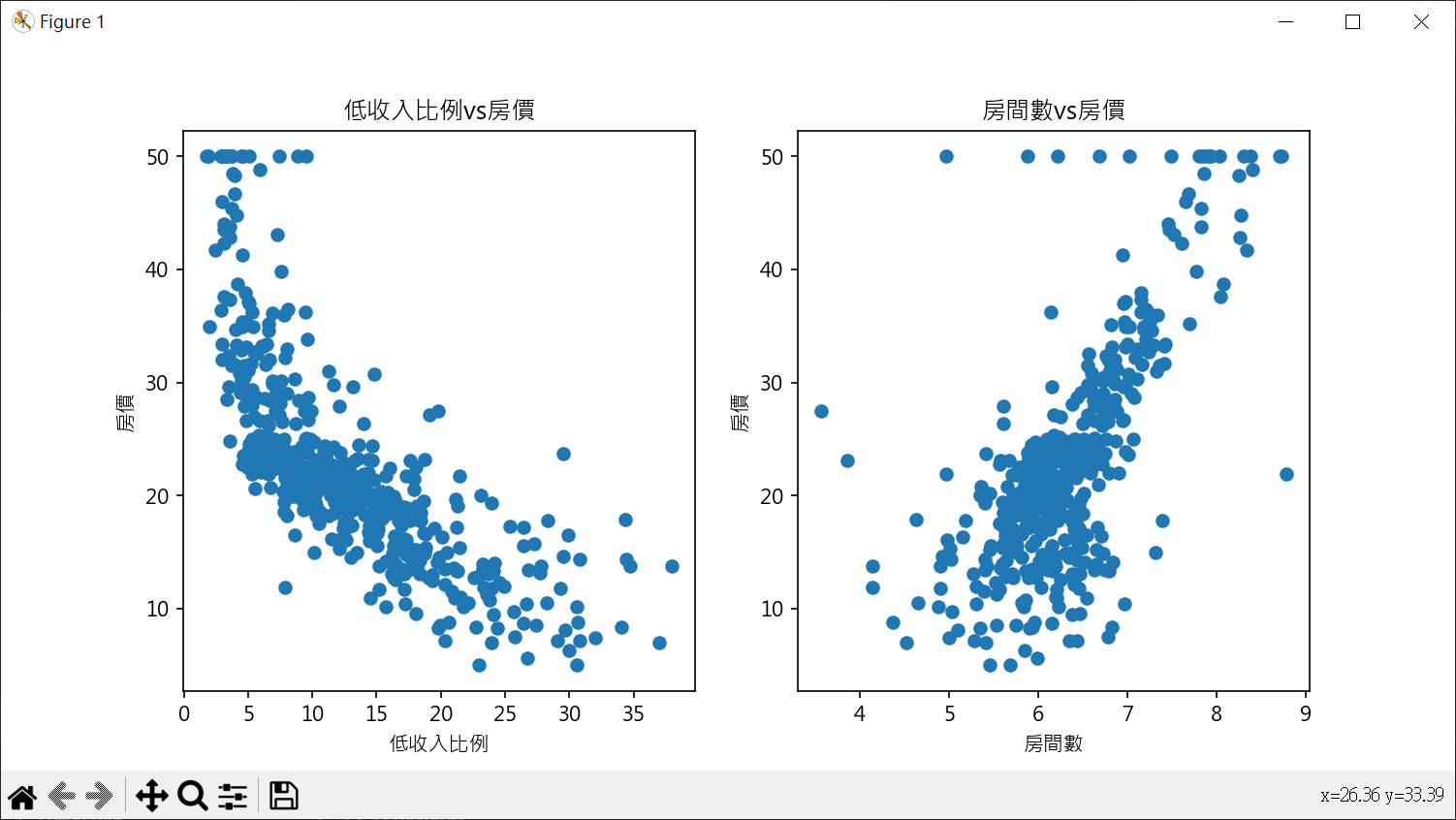
使用最相關特徵做房價預估 繪製散點圖 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 import pandas as pdimport matplotlib.pyplot as pltplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False boston = pd.read_csv("boston.csv" , sep='\s+' ) fig, axs = plt.subplots(nrows=1 , ncols=2 , figsize=(10 ,5 )) axs[0 ].scatter(boston['LSTAT' ], boston['MEDV' ]) axs[0 ].set_title("低收入比例vs房價" ) axs[0 ].set_xlabel("低收入比例" ) axs[0 ].set_ylabel("房價" ) axs[1 ].scatter(boston['RM' ], boston['MEDV' ]) axs[1 ].set_title("房間數vs房價" ) axs[1 ].set_xlabel("房間數" ) axs[1 ].set_ylabel("房價" ) plt.show()
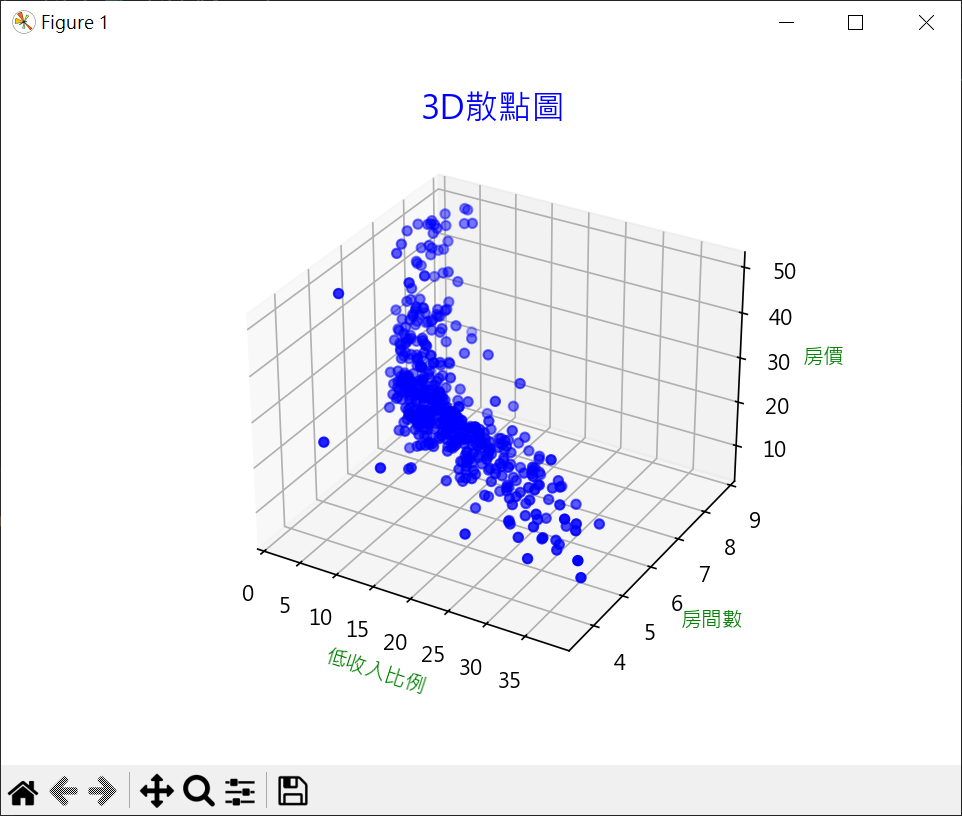
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 import pandas as pdimport matplotlib.pyplot as pltplt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False boston = pd.read_csv("boston.csv" , sep='\s+' ) fig = plt.figure() ax = fig.add_subplot(projection='3d' ) ax.scatter(boston['LSTAT' ], boston['RM' ], boston['MEDV' ], color='b' ) ax.set_title('3D散點圖' , fontsize=16 , color='b' ) ax.set_xlabel('低收入比例' , color='g' ) ax.set_ylabel('房間數' , color='g' ) ax.set_zlabel('房價' , color='g' ) plt.show()
獲得 R平方判定係數,截距與係數 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 import pandas as pdimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LinearRegressionfrom sklearn.metrics import r2_scorefrom joblib import dumpboston = pd.read_csv("boston.csv" , sep='\s+' ) X = pd.DataFrame(np.c_[boston['LSTAT' ], boston['RM' ]], columns=['LSTAT' , 'RM' ]) y = boston['MEDV' ] X_train, X_test, y_train, y_test = \ train_test_split(X, y, test_size=0.2 , random_state=1 ) model = LinearRegression() model.fit(X_train, y_train) intercept = model.intercept_ coefficients = model.coef_ print (f"y截距(b0) : {intercept:.3 f} " )print (f"斜率(b1,b2): {coefficients.round (3 )} " )formula = f"y = {intercept:.3 f} " for i, coef in enumerate (coefficients): formula += f" + ({coef:.3 f} )*x{i+1 } " print ("線性迴歸方程式:" )print (formula)y_pred = model.predict(X_test) print (f"R2_Score:{r2_score(y_test, y_pred):.3 f} " )dump(model, 'boston_model.joblib' )
計算預估房價 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 from joblib import loadimport pandas as pdimport numpy as npmodel = load('boston_model.joblib' ) lstat = eval (input ("請輸入低收入比例 : " )) rooms = eval (input ("請輸入房間數 :" )) data = pd.DataFrame(np.c_[[lstat], [rooms]], columns =['LSTAT' , 'RM' ]) price_pred = model.predict(data) print (f"用模型計算房價 : {price_pred[0 ]:.2 f} " )intercept = model.intercept_ coeff = model.coef_ price_cal = intercept + coeff[0 ] * lstat + coeff[1 ] * rooms print (f"用迴歸公式計算房價 : {price_cal:.2 f} " )
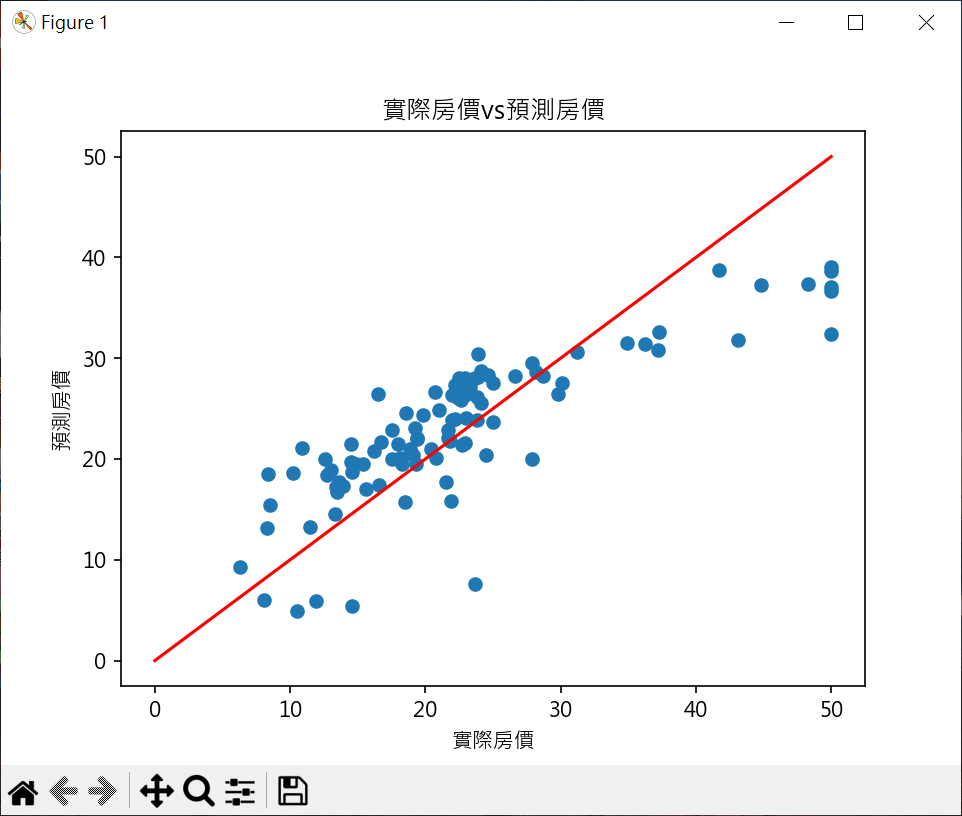
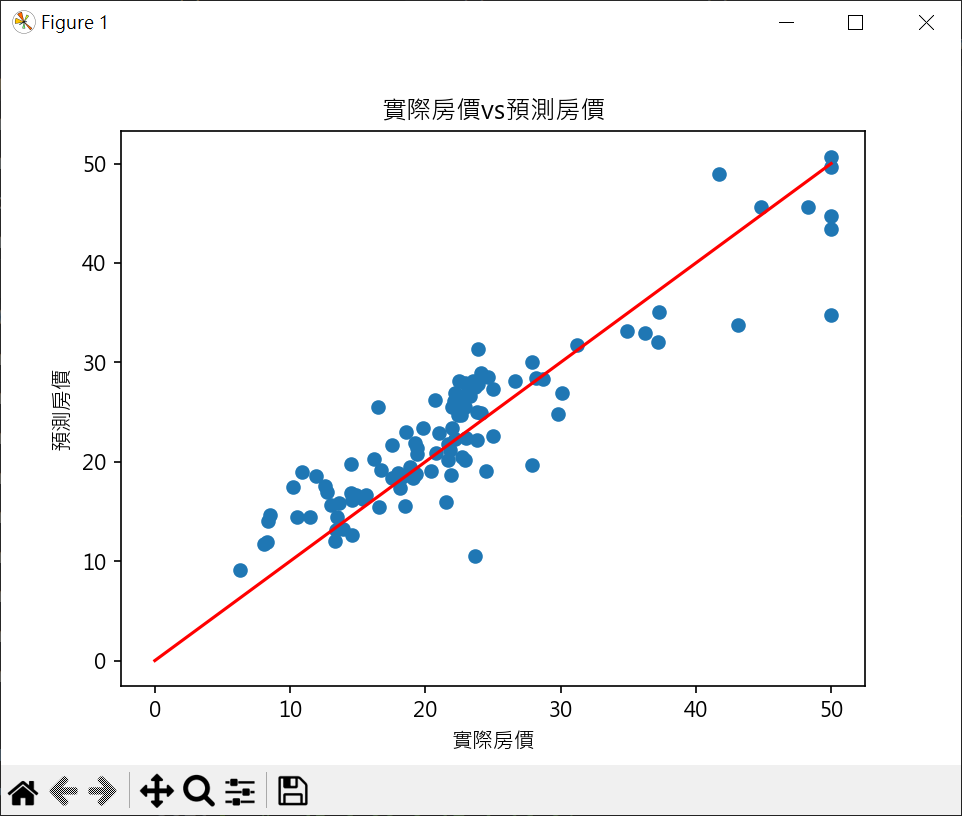
繪製實際房價與預估房價 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 import pandas as pdimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LinearRegressionimport matplotlib.pyplot as pltboston = pd.read_csv("boston.csv" , sep='\s+' ) X = pd.DataFrame(np.c_[boston['LSTAT' ], boston['RM' ]], columns=['LSTAT' , 'RM' ]) y = boston['MEDV' ] X_train, X_test, y_train, y_test = \ train_test_split(X, y, test_size=0.2 , random_state=1 ) model = LinearRegression() model.fit(X_train, y_train) y_pred = model.predict(X_test) print (f"真實房價\n {np.array(y_test.tolist())} " )print ("-" *70 )print (f"預測房價\n {y_pred.round (1 )} " )plt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False plt.scatter(y_test, y_pred) line_x = np.linspace(0 , 50 , 100 ) plt.plot(line_x, line_x, color='red' ) plt.title("實際房價vs預測房價" ) plt.xlabel("實際房價" ) plt.ylabel("預測房價" ) plt.show()
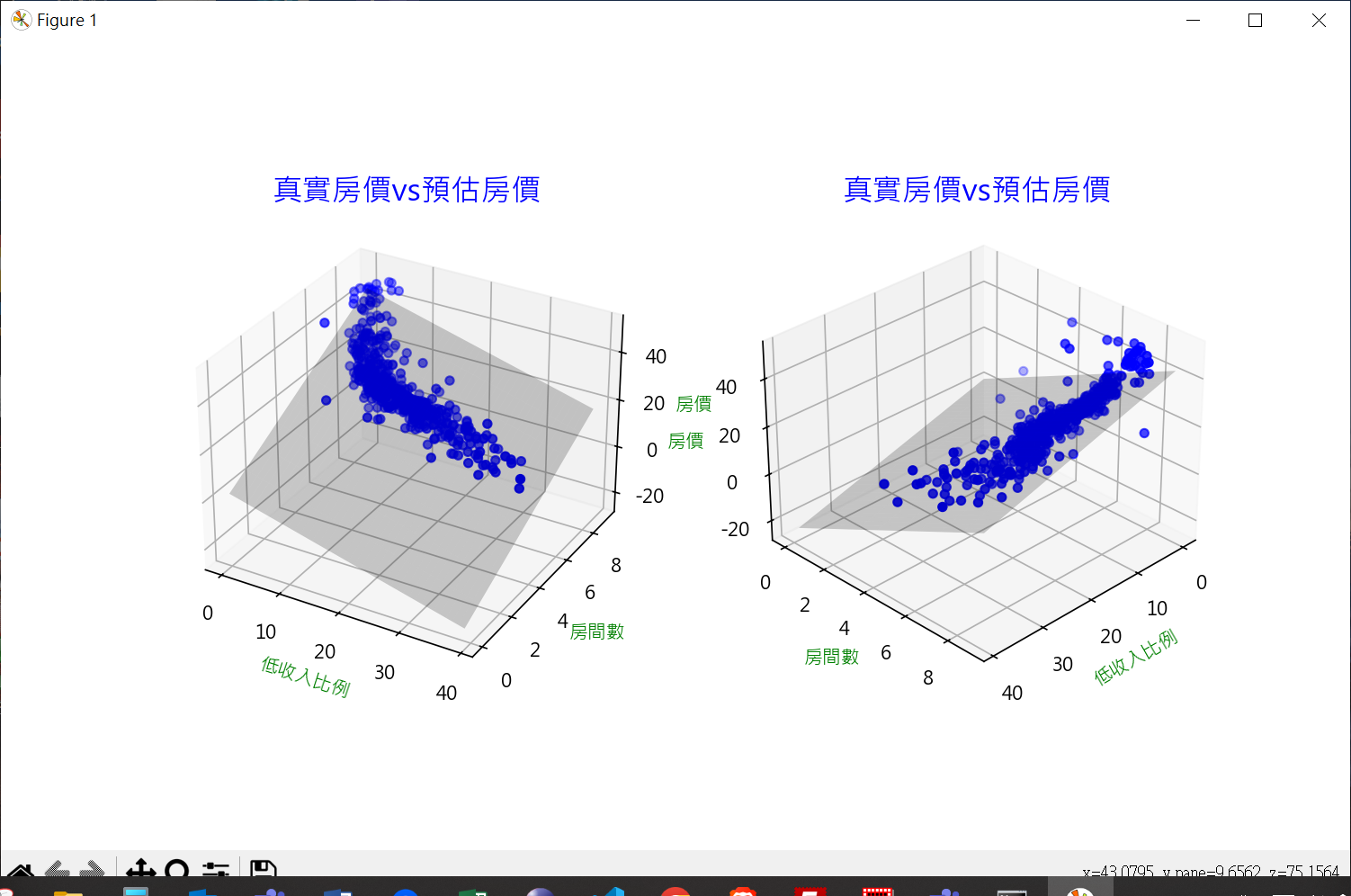
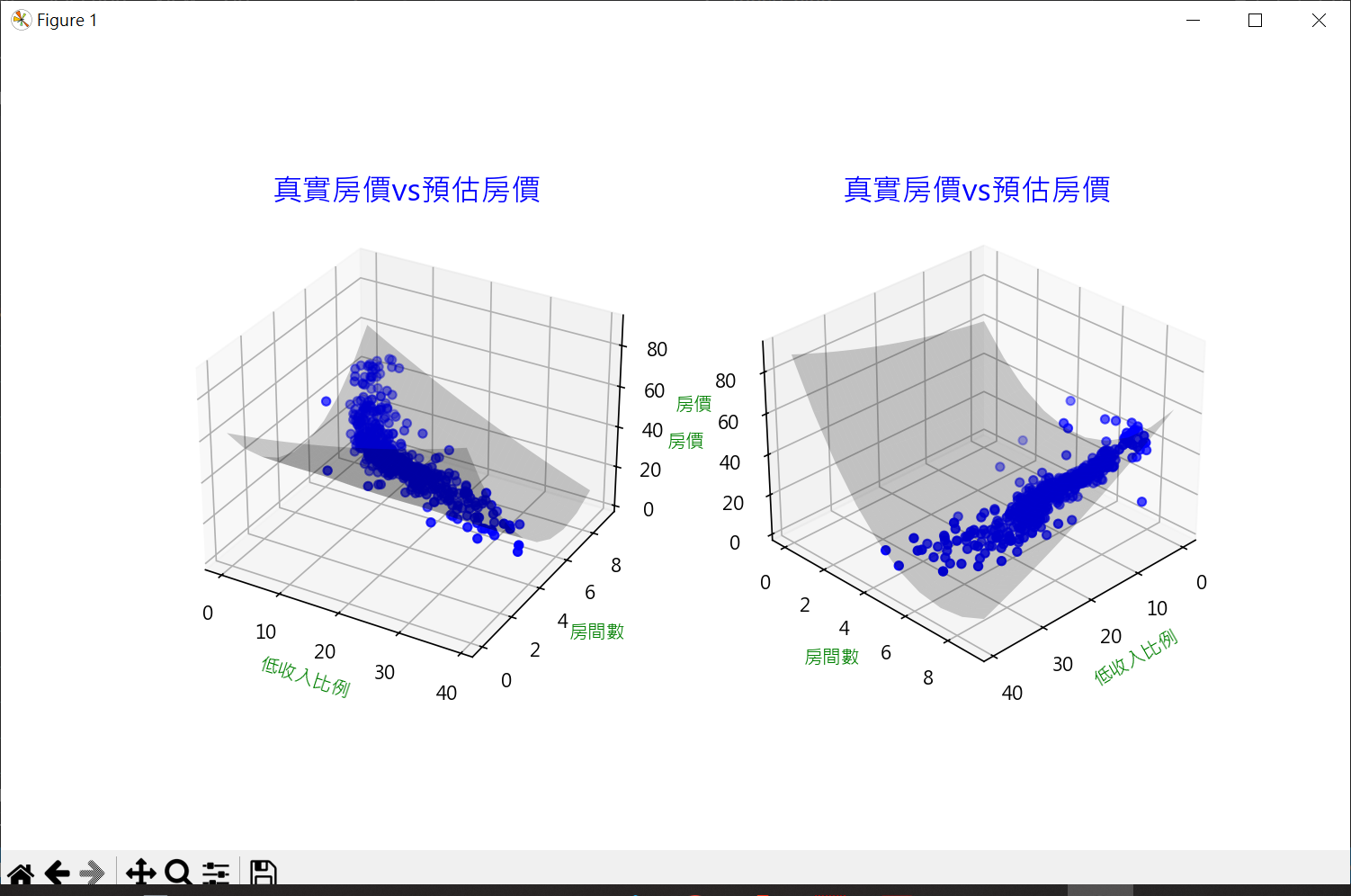
繪製3D實際房價與預估房價 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 import pandas as pdimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LinearRegressionimport matplotlib.pyplot as pltboston = pd.read_csv("boston.csv" , sep='\s+' ) X = pd.DataFrame(np.c_[boston['LSTAT' ], boston['RM' ]], columns=['LSTAT' , 'RM' ]) y = boston['MEDV' ] X_train, X_test, y_train, y_test = \ train_test_split(X, y, test_size=0.2 , random_state=1 ) model = LinearRegression() model.fit(X_train, y_train) y_pred = model.predict(X_test) print (f"真實房價\n {np.array(y_test.tolist())} " )print ("-" *70 )print (f"預測房價\n {y_pred.round (1 )} " )plt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False fig = plt.figure(figsize= (10 , 6 )) ax1 = fig.add_subplot(121 , projection='3d' ) ax2 = fig.add_subplot(122 , projection='3d' ) ax1.scatter(boston['LSTAT' ], boston['RM' ], boston['MEDV' ], color='b' ) x = np.arange(0 , 40 , 1 ) y = np.arange(0 , 10 , 1 ) x_surf1, y_surf1 = np.meshgrid(x, y) z = lambda x, y: (model.intercept_ + model.coef_[0 ]*x + model.coef_[1 ]*y) ax1.plot_surface(x_surf1, y_surf1, z(x_surf1, y_surf1), color='None' , alpha=0.2 ) ax1.set_title('真實房價vs預估房價' , fontsize=16 , color='b' ) ax1.set_xlabel('低收入比例' , color='g' ) ax1.set_ylabel('房間數' , color='g' ) ax1.set_zlabel('房價' , color='g' ) ax2.scatter(boston['LSTAT' ], boston['RM' ], boston['MEDV' ], color='b' ) ax2.plot_surface(x_surf1, y_surf1, z(x_surf1, y_surf1), color='None' , alpha=0.2 ) ax2.set_title('真實房價vs預估房價' , fontsize=16 , color='b' ) ax2.set_xlabel('低收入比例' , color='g' ) ax2.set_ylabel('房間數' , color='g' ) ax2.set_zlabel('房價' , color='g' ) ax2.view_init(elev=30 , azim=45 ) plt.show()
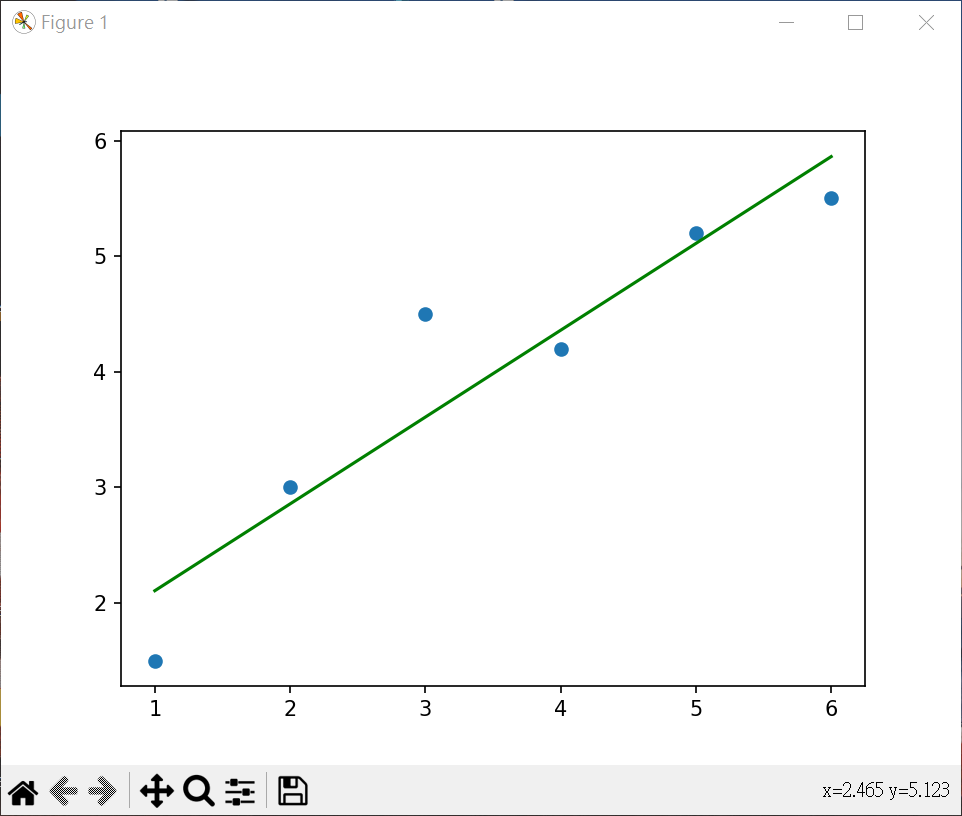
多項式迴歸 繪製散點圖及迴歸直線 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 import pandas as pdimport matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegressiondf = pd.read_csv('data23_19.csv' ) X = pd.DataFrame(df.x) y = df.y print (df)print (X)print (y)model = LinearRegression() model.fit(X,y) y_pred = model.predict(X) print (f"R2_score = {model.score(X, y):.3 f} " )plt.plot(X, y_pred, color='g' ) plt.scatter(df.x, df.y) plt.show()
生成一元二次特徵 fit_transform() 結合 fit() 和 transform():
fit() : 用於學習模型參數
transform() : 利用fit()得到的參數來變換數據
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 import numpy as npfrom sklearn.preprocessing import PolynomialFeaturesX = np.array([[1 ], [2 ], [3 ], [4 ]]) degree = 2 poly = PolynomialFeatures(degree) X_poly = poly.fit_transform(X) print (X)print (poly.get_feature_names_out(input_features=['x' ]))print (X_poly)degree = 4 poly4 = PolynomialFeatures(degree) X_poly4 = poly4.fit_transform(X) print (poly4.get_feature_names_out(input_features=['x' ]))print (X_poly4)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 import pandas as pdfrom sklearn.preprocessing import PolynomialFeaturesdf = pd.read_csv('data23_19.csv' ) X = pd.DataFrame(df.x) print (df)print (X)degree = 2 poly = PolynomialFeatures(degree) X_poly = poly.fit_transform(X) print (poly.get_feature_names_out())print (X_poly)
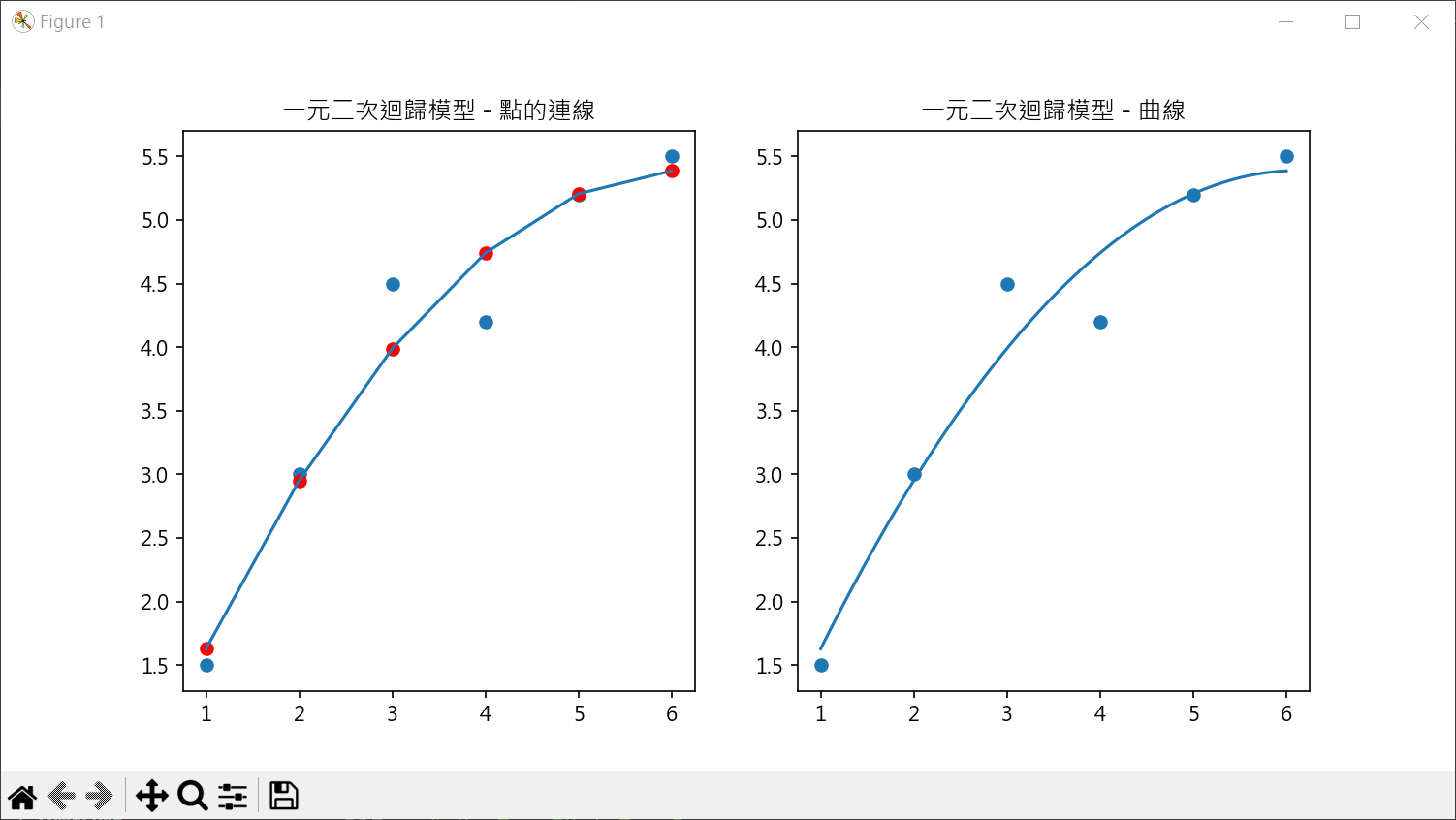
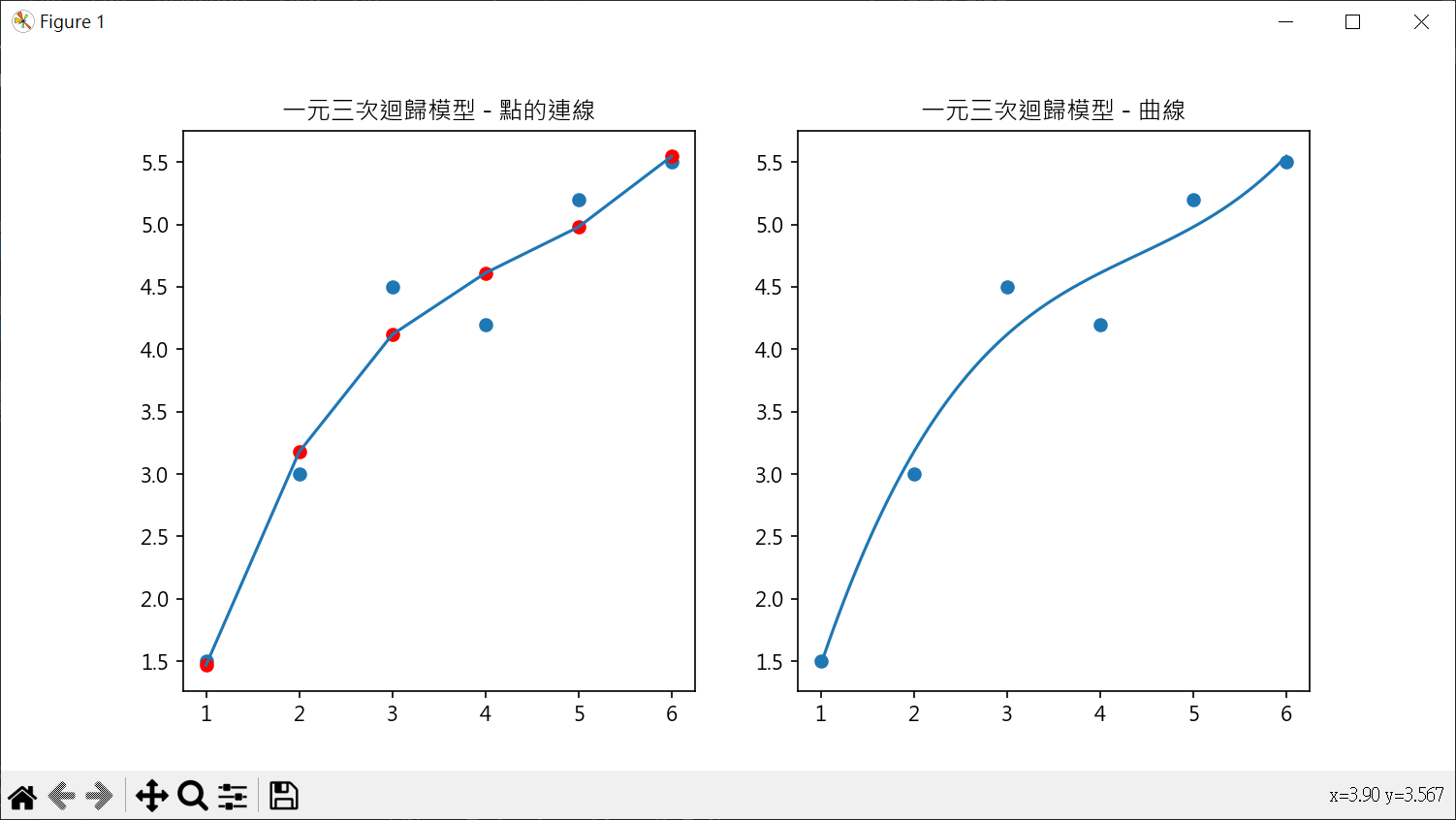
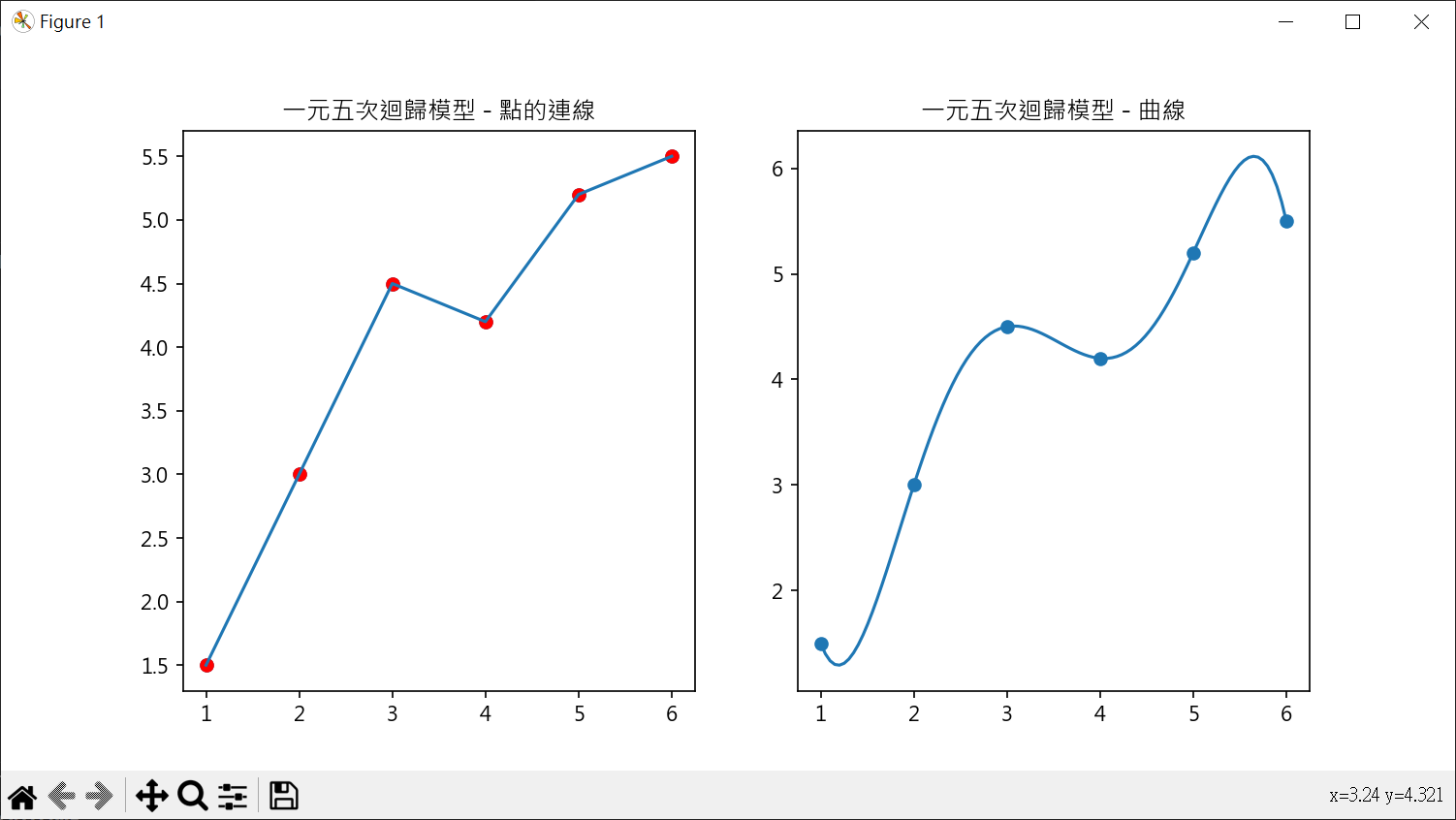
多項式特徵應用在 LinearRegression 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 import pandas as pdimport numpy as npfrom sklearn.preprocessing import PolynomialFeaturesfrom sklearn.linear_model import LinearRegressionimport matplotlib.pyplot as pltdf = pd.read_csv('data23_19.csv' ) X = pd.DataFrame(df.x) y = df.y degree = 5 poly = PolynomialFeatures(degree) X_poly = poly.fit_transform(X) model = LinearRegression() model.fit(X_poly, y) y_poly_pred = model.predict(X_poly) print (f"R2 score = {model.score(X_poly, y):.2 f} " )intercept = model.intercept_ coeff = model.coef_ print (f"截距 : {intercept:.3 f} " )print (f"係數 : {coeff.round (3 )} " )plt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False fig, axs = plt.subplots(nrows=1 , ncols=2 , figsize=(10 ,5 )) axs[0 ].scatter(X, y) axs[0 ].scatter(X, y_poly_pred, color='r' ) axs[0 ].plot(X, y_poly_pred) axs[0 ].set_title("一元五次迴歸模型 - 點的連線" ) xx = np.linspace(1 , 6 , 100 ) y_curf = lambda x: (intercept + coeff[1 ]*x + coeff[2 ]*x**2 + coeff[3 ]*x**3 + coeff[4 ]*x**4 + coeff[5 ]*x**5 ) axs[1 ].plot(xx, y_curf(xx)) axs[1 ].scatter(X, y) axs[1 ].set_title("一元五次迴歸模型 - 曲線" ) plt.show()
機器學習的理想模型
使用二元二次方程式做房價預估 計算 R score 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 import pandas as pdimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LinearRegressionfrom sklearn.preprocessing import PolynomialFeaturesfrom sklearn.metrics import r2_scorefrom joblib import dumpboston = pd.read_csv("boston.csv" , sep='\s+' ) X = pd.DataFrame(np.c_[boston['LSTAT' ], boston['RM' ]], columns=['LSTAT' , 'RM' ]) y = boston['MEDV' ] X_train, X_test, y_train, y_test = \ train_test_split(X, y, test_size=0.2 , random_state=1 ) degree = 2 poly = PolynomialFeatures(degree) X_train_poly = poly.fit_transform(X_train) X_test_poly = poly.transform(X_test) model = LinearRegression() model.fit(X_train_poly, y_train) print (f"R score : {model.score(X_test_poly, y_test)} " )intercept = model.intercept_ coeff = model.coef_ print (f"截距 : {intercept} " )print (poly.get_feature_names_out())print (f"係數 : {coeff} " )
計算預估房價 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 import pandas as pdimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LinearRegressionfrom sklearn.preprocessing import PolynomialFeaturesfrom sklearn.metrics import r2_scorefrom joblib import dumpimport matplotlib.pyplot as pltboston = pd.read_csv("boston.csv" , sep='\s+' ) X = pd.DataFrame(np.c_[boston['LSTAT' ], boston['RM' ]], columns=['LSTAT' , 'RM' ]) y = boston['MEDV' ] X_train, X_test, y_train, y_test = \ train_test_split(X, y, test_size=0.2 , random_state=1 ) degree = 2 poly = PolynomialFeatures(degree) X_train_poly = poly.fit_transform(X_train) X_test_poly = poly.transform(X_test) model = LinearRegression() model.fit(X_train_poly, y_train) y_pred = model.predict(X_test_poly) print (f"實際房價\n{np.array(y_test.tolist())} " )print ("-" *70 )print (f"預估房價\n{y_pred.round (1 )} " )plt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False plt.scatter(y_test, y_pred) line_x = np.linspace(0 , 50 , 100 ) plt.plot(line_x, line_x, color='red' ) plt.title("實際房價vs預測房價" ) plt.xlabel("實際房價" ) plt.ylabel("預測房價" ) plt.show()
繪製3D實際房價vs預估房價 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 import pandas as pdimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LinearRegressionfrom sklearn.preprocessing import PolynomialFeaturesfrom sklearn.metrics import r2_scorefrom joblib import dumpimport matplotlib.pyplot as pltboston = pd.read_csv("boston.csv" , sep='\s+' ) X = pd.DataFrame(np.c_[boston['LSTAT' ], boston['RM' ]], columns=['LSTAT' , 'RM' ]) y = boston['MEDV' ] X_train, X_test, y_train, y_test = \ train_test_split(X, y, test_size=0.2 , random_state=1 ) degree = 2 poly = PolynomialFeatures(degree) X_train_poly = poly.fit_transform(X_train) model = LinearRegression() model.fit(X_train_poly, y_train) intercept = model.intercept_ coeff = model.coef_ plt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False fig = plt.figure(figsize= (10 , 6 )) ax1 = fig.add_subplot(121 , projection='3d' ) ax2 = fig.add_subplot(122 , projection='3d' ) ax1.scatter(boston['LSTAT' ], boston['RM' ], boston['MEDV' ], color='b' ) x = np.arange(0 , 40 , 1 ) y = np.arange(0 , 10 , 1 ) x_surf1, y_surf1 = np.meshgrid(x, y) z = lambda x, y: (model.intercept_ + \ model.coef_[1 ]*x + \ model.coef_[2 ]*y + \ model.coef_[3 ]*x**2 + \ model.coef_[4 ]*x*y + \ model.coef_[5 ]*y**2 ) ax1.plot_surface(x_surf1, y_surf1, z(x_surf1, y_surf1), color='None' , alpha=0.2 ) ax1.set_title('真實房價vs預估房價' , fontsize=16 , color='b' ) ax1.set_xlabel('低收入比例' , color='g' ) ax1.set_ylabel('房間數' , color='g' ) ax1.set_zlabel('房價' , color='g' ) ax2.scatter(boston['LSTAT' ], boston['RM' ], boston['MEDV' ], color='b' ) ax2.plot_surface(x_surf1, y_surf1, z(x_surf1, y_surf1), color='None' , alpha=0.2 ) ax2.set_title('真實房價vs預估房價' , fontsize=16 , color='b' ) ax2.set_xlabel('低收入比例' , color='g' ) ax2.set_ylabel('房間數' , color='g' ) ax2.set_zlabel('房價' , color='g' ) ax2.view_init(elev=30 , azim=45 ) plt.show()
用所有的特徵執行波士頓房價預估
使用所有的特徵值並未得到較好的預估結果
使用2個特徵的二次多項式得到較好的結果
較簡單的模型在預測未出現的數據有時表現得更好
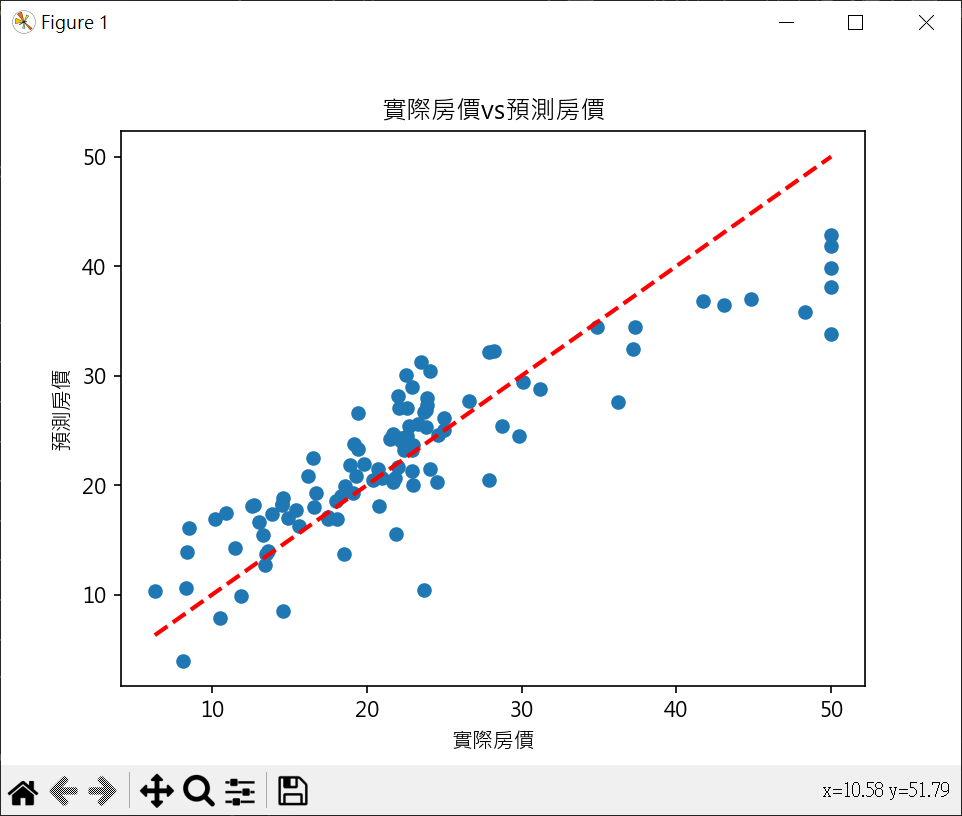
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 import pandas as pdimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LinearRegressionfrom sklearn.preprocessing import PolynomialFeaturesfrom sklearn.metrics import r2_score, mean_squared_errorfrom joblib import dumpimport matplotlib.pyplot as pltboston = pd.read_csv("boston.csv" , sep='\s+' ) X = boston.drop('MEDV' , axis=1 ) y = boston['MEDV' ] X_train, X_test, y_train, y_test = \ train_test_split(X, y, test_size=0.2 , random_state=1 ) model = LinearRegression() model.fit(X_train, y_train) y_pred = model.predict(X_test) r2 = r2_score(y_test, y_pred) print (f"R score : {r2.round (3 )} " )mse = mean_squared_error(y_test, y_pred) print (f"Mean Squared Error(MSE) : {mse.round (3 )} " )intercept = model.intercept_ coeff = model.coef_ print (f"截距 : {intercept:.3 f} " )print (f"係數 : {coeff.round (3 )} " )print ("-" *70 )print (f"實際房價\n{np.array(y_test.tolist())} " )print ("-" *70 )print (f"預估房價\n{y_pred.round (1 )} " )plt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False plt.scatter(y_test, y_pred) plt.plot([min (y_test),max (y_test)], [min (y_test),max (y_test)], color='red' , linestyle='--' , lw=2 ) plt.title("實際房價vs預測房價" ) plt.xlabel("實際房價" ) plt.ylabel("預測房價" ) plt.show()
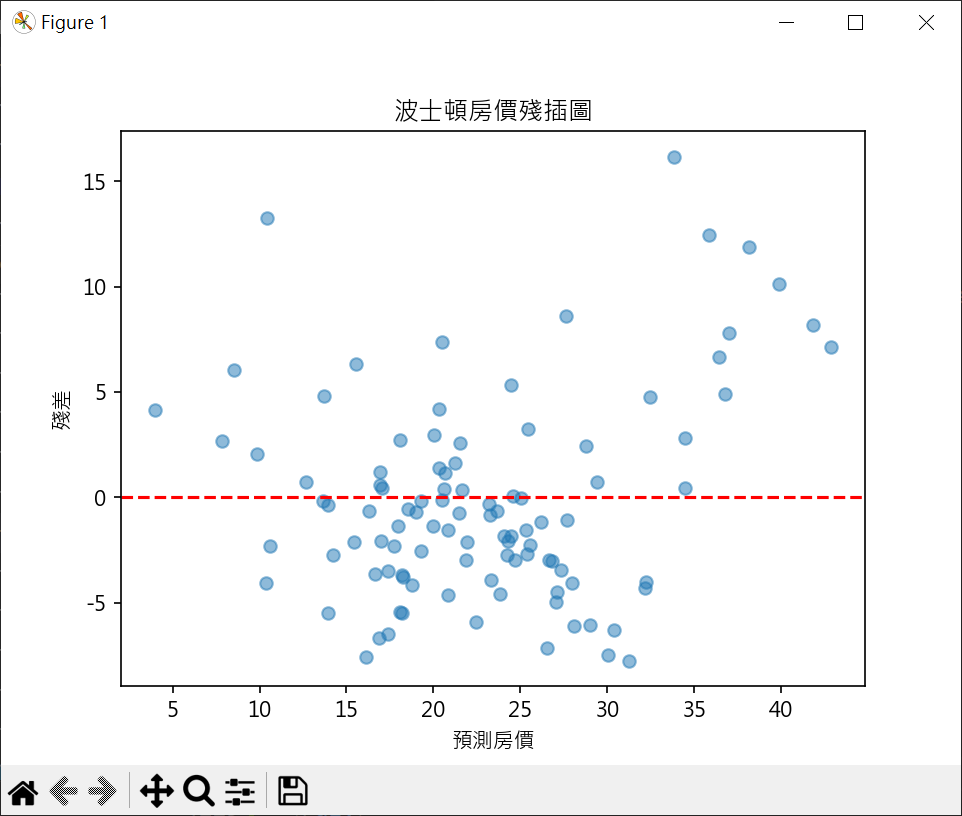
殘差圖(Residual Plot)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 import pandas as pdimport numpy as npfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LinearRegressionfrom sklearn.preprocessing import PolynomialFeaturesfrom sklearn.metrics import r2_score, mean_squared_errorfrom joblib import dumpimport matplotlib.pyplot as pltboston = pd.read_csv("boston.csv" , sep='\s+' ) X = boston.drop('MEDV' , axis=1 ) y = boston['MEDV' ] X_train, X_test, y_train, y_test = \ train_test_split(X, y, test_size=0.2 , random_state=1 ) model = LinearRegression() model.fit(X_train, y_train) y_pred = model.predict(X_test) residuals = y_test - y_pred plt.rcParams["font.family" ] = ["Microsoft JhengHei" ] plt.rcParams["axes.unicode_minus" ] = False plt.scatter(y_pred, residuals, alpha=0.5 ) plt.axhline(y=0 , color='r' , linestyle='--' ) plt.title("波士頓房價殘插圖" ) plt.xlabel("預測房價" ) plt.ylabel("殘差" ) plt.show()
梯度下降迴歸 SGDRegressor()
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 import pandas as pdfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LinearRegressionfrom sklearn.metrics import r2_score, mean_squared_errorfrom sklearn.linear_model import SGDRegressorfrom sklearn.preprocessing import StandardScalerboston = pd.read_csv("boston.csv" , sep='\s+' ) X = boston.drop('MEDV' , axis=1 ) y = boston['MEDV' ] X_train, X_test, y_train, y_test = \ train_test_split(X, y, test_size=0.2 , random_state=1 ) scaler = StandardScaler() X_train = scaler.fit_transform(X_train) X_test = scaler.transform(X_test) sgd_regressor = SGDRegressor(max_iter=1000 , random_state=1 ) sgd_regressor.fit(X_train, y_train) y_pred = sgd_regressor.predict(X_test) y_train_pred = sgd_regressor.predict(X_train) r2_train = r2_score(y_train, y_train_pred) print (f"訓練數據的R平方係數 : {r2_train.round (3 )} " )r2_test = r2_score(y_test, y_pred) print (f"測試數據的R平方係數 : {r2_test.round (3 )} " )mse = mean_squared_error(y_test, y_pred) print (f"模型的性能指標(MSE) : {mse.round (3 )} " )