CS50AI

發表於 更新於 分類於 Disqus：
文章字數： 30k 所需閱讀時間 ≈ 27 分鐘

Term

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
agent
state
initial state
actions
  (s)
transition model
  result(s,a)
path cost
solution
 potional solution

search problems:
 initiation state
 action
 transition model 
 goal test 
 path cost function

node :
 a dat structure that keeps track of
 -  a state
 - a parent (node that generate this node)
 - a action (action applied to parent to get node)
 - a path cost(from initial state to node)

depth-first search (stack)
breadth-first search (queue)

uninformed search
infomed search
  greedy best-first search
  A* search

adversarial search : 對抗性搜索
Minimax
 Max(X) aims to maximize score
 MIN(O)  aimes to minize score
Alpha-Beta Pruning:不要找完下層所有
Depth-Limited Minimax:預估最大深度
  evaluation function

shell

1
2
3
4
5
6
# install
pip3 install -r requirements.txt
python.exe -m pip install --upgrade pip

# select python
Ctrl+Shift+P --> python interpreter --> select ...

project submit

put to github
1
2
3
4
5
6
7
8
9
10
# degress git
git init
git add .
git commit -m "first version"

# github create repository
# push to github
D:\work\run\me50-ai50\degrees>git remote add origin https://github.com/hot5656/cs50ai-degrees.git
git push -u origin master
# add brench ai50/projects/2024/x/degrees from github
submit
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# switch to new brance
git fetch
	From https://github.com/hot5656/cs50ai-p4-nim
	 * [new branch]      ai50/projects/2024/x/nim -> origin/ai50/projects/2024/x/nim

git checkout ai50/projects/2024/x/nim
	Switched to a new branch 'ai50/projects/2024/x/nim'
	branch 'ai50/projects/2024/x/nim' set up to track 'origin/ai50/projects/2024/x/nim'.

git branch -r
  origin/ai50/projects/2024/x/nim
  origin/master

# push for submit
git push -u https://github.com/me50/hot5656 ai50/projects/2024/x/degrees
    Username for 'https://github.com': hot5656
    Password for 'https://hot5656@github.com':
    Enumerating objects: 9, done.
    Counting objects: 100% (9/9), done.
    Delta compression using up to 8 threads
    Compressing objects: 100% (8/8), done.
    Writing objects: 100% (9/9), 3.04 KiB | 445.00 KiB/s, done.
    Total 9 (delta 0), reused 0 (delta 0), pack-reused 0
    remote:
    remote: Create a pull request for 'ai50/projects/2024/x/degrees' on GitHub by visiting:
    remote:      https://github.com/me50/hot5656/pull/new/ai50/projects/2024/x/degrees
    remote:
    To https://github.com/me50/hot5656
    * [new branch]      ai50/projects/2024/x/degrees -> ai50/projects/2024/x/degrees
    branch 'ai50/projects/2024/x/degrees' set up to track 'https://github.com/me50/hot5656/ai50/projects/2024/x/degrees'.
# check submit status
modify then submit
1
2
3
4
# tictactoe
git add .
git commit -m "add action exception"
git push -u https://github.com/me50/hot5656 ai50/projects/2024/x/tictactoe
update my repository
1
2
# push to my repository
git push -u https://github.com/me50/hot5656 ai50/projects/2024/x/tictactoe

knowledge

Term

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Entailment (語義蘊涵也叫做邏輯蘊涵⊨)
α ⊨ β : In every model in which sentence α is true, sentence β is also true.

# inference 推論
P: It is a Tuesday.
Q: It is raining.
R: Harry will go for a run.
KB: (P ∧ ¬Q) --> R 
Inference: R

# Inference Algorithms (推理演算法)
#Model Checking(列舉所有)
• To determine if KB ⊨ α:
	• Enumerate all possible models.
	• If in every model where KB is true, α is true, then
	KB entails α.
	• Otherwise, KB does not entail α.
1
2
3
4
5
6
7
8
9
10
11
12
13
# →
P     Q     P → Q
false false true
false true 	true
true 	false false
true 	true 	true

# ↔
P  		Q  		P ↔ Q
false false	true
false true  false
true 	false false
true	true 	true

example code

rain?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from logic import *

rain = Symbol("rain")
hargrid = Symbol("hagrid")
dombledore = Symbol("dombledore")

sentence = And(rain, hargrid)
print(sentence.formula())	# rain ∧ hagrid

knowledge = Implication(Not(rain), hargrid)
print(knowledge.formula()) # (¬rain) => hagrid

# chaeck rain
knowledge = And(
    Implication(Not(rain), hargrid),
    Or(hargrid, dumbledore),
    Not(And(hargrid, dumbledore)),
    dumbledore
)
# print(knowledge.formula())
print(model_check(knowledge, rain)) # True
# print(model_check(knowledge, hargrid)) # False
# print(model_check(knowledge, dumbledore)) # True
clue
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import termcolor

from logic import *

mustard = Symbol("ColMustard")
plum = Symbol("ProfPlum")
scarlet = Symbol("MsScarlet")
characters = [mustard, plum, scarlet]

ballroom = Symbol("ballroom")
kitchen = Symbol("kitchen")
library = Symbol("library")
rooms = [ballroom, kitchen, library]

knife = Symbol("knife")
revolver = Symbol("revolver")
wrench = Symbol("wrench")
weapons = [knife, revolver, wrench]

symbols = characters + rooms + weapons


def check_knowledge(knowledge):
    for symbol in symbols:
        if model_check(knowledge, symbol):
            termcolor.cprint(f"{symbol}: YES", "green")
        elif not model_check(knowledge, Not(symbol)):
            print(f"{symbol}: MAYBE")

knowledge = And(
    Or(mustard, plum, scarlet),
    Or(ballroom, kitchen, library),
    Or(knife, revolver, wrench),
)

# print(knowledge.formula())

knowledge.add(Not(mustard))
knowledge.add(Not(kitchen))
knowledge.add(Not(revolver))

knowledge.add(Or(
    Not(scarlet), Not(library), Not(wrench)
))

knowledge.add(Not(plum))
knowledge.add(Not(ballroom))

check_knowledge(knowledge)

Inference Rules(推理規則)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# modus ponens 正向思維律
a → B  --> a true so B true
# and Elimination 和消除
a∧B --> a true, B true
# double negation Elimination 雙重否定
¬(¬α)  --> α
# Implication Elimination 暗示消除
α → β --> ¬α ∨ β
# Bicoditional Elimination
α ↔ β --> (α → β) ∧ (β → α)
# De morgan's Law
¬(α ∧ β) --> ¬α ∨ ¬β
¬(α ∨ β) --> ¬α ∧ ¬β
# Distributive Property 分配律
(α ∧ (β ∨ γ)) --> (α ∧ β) ∨ (α ∧ γ)
(α ∨ (β ∧ γ)) --> (α ∨ β) ∧ (α ∨ γ)

Theorem Proving(定理證明)

1
2
3
4
5
• initial state: starting knowledge base
• actions: inference rules
• transition model: new knowledge base after inference
• goal test: check statement we're trying to prove
• path cost function: number of steps in proof

Resolution(歸結原理)

1
2
3
4
(P ∨ Q) (¬P) --> Q
(P ∨ Q1 ∨ Q2 ∨ ...∨ Qn) (¬P) --> Q1 ∨ Q2 ∨ ...∨ Qn
(P ∨ Q) (¬P ∨ R) --> Q ∨ R
(P ∨ Q1 ∨ Q2 ∨ ...∨ Qn) (¬P ∨ R1 ∨ R2 ∨ ...∨ Rm) --> Q1 ∨ Q2 ∨ ...∨ Qn ∨ R1 ∨ R2 ∨ ...∨ Rm

Conversion to CNF

1
2
3
4
5
6
7
# Clauses allow us to convert any logical statement into a Conjunctive Normal Form (CNF), which is a conjunction of clauses, for example: (A ∨ B ∨ C) ∧ (D ∨ ¬E) ∧ (F ∨ G).
# example 
Conversion to CNF
(P ∨ Q) → R
¬(P ∨ Q) ∨ R					# eliminate implication
(¬P ∧ ¬Q) ∨ R					# De Morgan's Law
(¬P ∨ R) ∧ (¬Q ∨ R)	  # distributive law

Inference by Resolution

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
(P ∨ Q) (¬P ∨ R) --> (Q ∨ R)
(P ∨ Q ∨ S) (¬P ∨ R ∨ S) --> (Q ∨ S ∨ R)
P ¬P --> Flase

• To determine if KB ⊨ α:
	• Check if (KB ∧ ¬α) is a contradiction?
	• If so, then KB ⊨ α.
	• Otherwise, no entailment.

• To determine if KB ⊨ α:
	• Convert (KB ∧ ¬α) to Conjunctive Normal Form.
	• Keep checking to see if we can use resolution to
	produce a new clause.
	• If ever we produce the empty clause (equivalent
	to False), we have a contradiction, and KB ⊨ α.
	• Otherwise, if we can't add new clauses, no
	entailment.

# Does (A ∨ B) ∧ (¬B ∨ C) ∧ (¬C) entail A?

First-Order Logic

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
First-Order Logic 
Constant Symbol Predicate Symbol
Minerva					Person
Pomona					House
Horace					BelongsTo
Gilderoy
Gryffindor
Hufflepuff
Ravenclaw
Slytherin
Person(Minerva) 									Minerva is a person.
House(Gryffindor) 								Gryffindor is a house.
¬House(Minerva) 									Minerva is not a house.
BelongsTo(Minerva, Gryffindor)		Minerva belongs to Gryffindor
# Universal Quantification
# ∀表所有人
∀x. BelongsTo(x, Gryffindor) →  ¬BelongsTo(x, Hufflepuff)
# Existential Quantification
# ∃任一存在
∃x. House(x) ∧ BelongsTo(Minerva, x)
∀x. Person(x) → (∃y. House(y) ∧ BelongsTo(x, y)

Uncertainty

Conditional Probability 條件機率

1
2
3
4
5
6
7
8
9
P(a|b) = P(a∧b)/P(b)
	a=red-6, b=blue-6
	P(a∧b) = 1/36
	P(b) = 1/6
	P(a|b) = 1/6

P(a^b) = P(b) * P(a|b)
P(a^b) = P(a) * P(b|a)
P(a) * P(b|a) = P(b) * P(a|b)

Bayes’ Rule(貝葉斯法則)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
	P(a|b) = P(a∧b)/P(b)

	P(a^b) = P(b) * P(a|b)
	P(a^b) = P(a) * P(b|a)
	P(a) * P(b|a) = P(b) * P(a|b)
	P(b|a) = P(b) * P(a|b)/P(a)

- 80% of rainy afternoons start with cloudy mornings, or P(clouds | rain).
- 40% of days have cloudy mornings, or P(clouds).
- 10% of days have rainy afternoons, or P(rain).

P(rain|clouds) = P(clouds|rain) * P(rain)/P(cloud)
               = (.8)(.1)/.4 = 0.2

Knowing 
  P(visible effect | unknow cause)
We can calculate 
  P(unknow cause | visible effect)

Knowing 
  P(medical test result | disease)
We can calculate 
  P(disease |  medical test resul)

Joint Probability(聯合機率)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
C = cloud C = ¬cloud
0.4				0.6
R = rain 	R = ¬rain
0.1				0.9
 
						R = rain 	R = ¬rain
C = cloud		0.08			0.32
C = ¬cloud	0.02			0.58

# , = and 
# p(rain) constant
P(C|rain) = P(C,rain)/P(rain)
					= αP(C, rain)
          = α<0.08, 0.02> = <0.8 0.2>

Probability Rules(機率規則)

1
2
3
4
5
6
7
8
9
Negation: P(¬a) = 1 - P(a). 
Inclusion-Exclusion: P(a ∨ b) = P(a) + P(b) - P(a ∧ b). 
Marginalization: P(a) = P(a, b) + P(a, ¬b). 

# Marginalization formula
P(X = xi) = ∑P(X = xi, Y = yj)
            j
 P(C = cloud) = P(C = cloud, R = rain) + P(C = cloud, R = ¬rain) 
              = 0.08 + 0.32 = 0.4

Bayesian Networks(貝葉斯網絡)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
- They are directed graphs.
- Each node on the graph represent a random variable.
- An arrow from X to Y represents that X is a parent of Y. That is, the probability distribution of Y depends on the value of X.
- Each node X has probability distribution P(X | Parents(X)).

# Rain 
none 	light heavy
0.7		0.2		0.1

# Maintenance 
R    	yes 	no
none	0.4		0.6
light	0.2		0.8
heavy	0.1		0.9

# Train 
R 		M 	on time delayed
none	yes	0.8			0.2
none	no	0.9			0.1
light	yes	0.6			0.4
light	no	0.7			0.3
heavy	yes	0.4			0.6
heavy	no	0.5			0.5

# Appointment is a random variable 
T				attend	miss
on time	0.9			0.1
delayed	0.6			0.4

Inference

1
2
3
4
5
6
7
8
- Query X: the variable for which we want to compute the probability distribution.
- Evidence variables E: one or more variables that have been observed for event e. For example, we might have observed that there is 
	light rain, and this observation helps us compute the probability that the train is delayed.
- Hidden variables Y: variables that aren’t the query and also haven’t been observed. For example, standing at the train station, we 
	can observe whether there is rain, but we can’t know if there is maintenance on the track further down the road. Thus, Maintenance 
	would be a hidden variable in this situation.
- The goal: calculate P(X | e). For example, compute the probability distribution of the Train variable (the query) based on the 
	evidence e that we know there is light rain.

Bayesian Networks

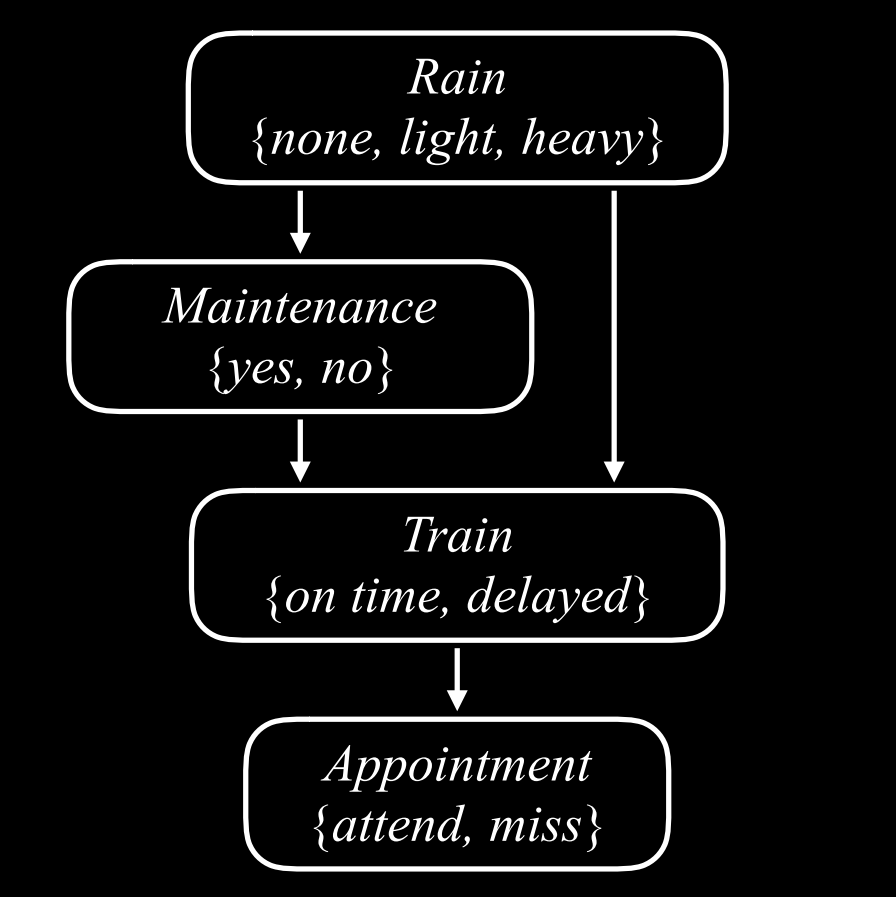
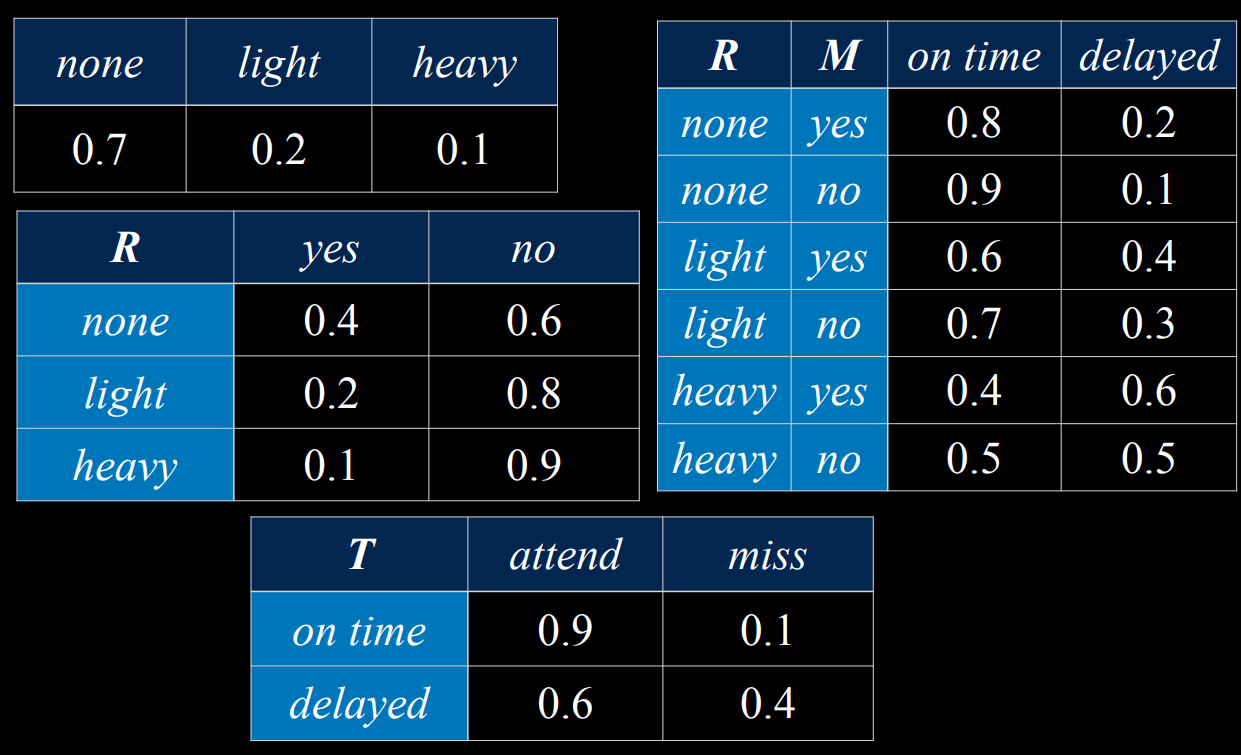
inastall pomegranate (need correct version)
1
pip3 install pomegranate==v0.14.9
Inference by Enumeration列舉 #1 - give condition –> attend/miss probability
model.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from pomegranate import *

# Rain node has no parents
rain = Node(DiscreteDistribution({
    "none": 0.7,
    "light": 0.2,
    "heavy": 0.1
}), name="rain")

......

# Create a Bayesian Network and add states
model = BayesianNetwork()
model.add_states(rain, maintenance, train, appointment)

# Add edges connecting nodes
model.add_edge(rain, maintenance)
model.add_edge(rain, train)
model.add_edge(maintenance, train)
model.add_edge(train, appointment)

# Finalize model
model.bake()
likelihood.py
1
2
3
4
5
6
7
8
from model import model

# Calculate probability for a given observation
probability = model.probability([["none", "no", "on time", "attend"]])
probability_miss = model.probability([["none", "no", "on time", "miss"]])

print("normal attend ", probability)
print("normal miss ", probability_miss)
result
1
2
3
python .\likelihood.py
	normal attend  0.34019999999999995
	normal miss  0.037800000000000014
Inference by Enumeration #2 - train delayed –> predict attend/miss probability
inference.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from model import model

# Calculate predictions
# predictions = model.predict_proba({
#     "train": "delayed"
# })
# rain
#     none: 0.4583
#     light: 0.3069
#     heavy: 0.2348
# maintenance
#     no: 0.6432
#     yes: 0.3568
# train: delayed
# appointment
#     miss: 0.4000
#     attend: 0.6000

predictions = model.predict_proba({
    "rain":"heavy",
    "train": "delayed"
})
# rain: heavy
# maintenance
#     yes: 0.1176
#     no: 0.8824
# train: delayed
# appointment
#     attend: 0.6000
#     miss: 0.4000


# Print predictions for each node
for node, prediction in zip(model.states, predictions):
    if isinstance(prediction, str):
        print(f"{node.name}: {prediction}")
    else:
        print(f"{node.name}")
        for value, probability in prediction.parameters[0].items():
            print(f"    {value}: {probability:.4f}")
Sampling取樣 - approximate inference 近似推理
sample.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import pomegranate

from collections import Counter

from model import model

def generate_sample():

    # Mapping of random variable name to sample generated
    sample = {}

    # Mapping of distribution to sample generated
    parents = {}

    # Loop over all states, assuming topological order
    for state in model.states:

        # If we have a non-root node, sample conditional on parents
        if isinstance(state.distribution, pomegranate.ConditionalProbabilityTable):
            sample[state.name] = state.distribution.sample(parent_values=parents)

        # Otherwise, just sample from the distribution alone
        else:
            sample[state.name] = state.distribution.sample()

        # Keep track of the sampled value in the parents mapping
        parents[state.distribution] = sample[state.name]

    # Return generated sample
    return sample

# Rejection sampling
# Compute distribution of Appointment given that train is delayed
N = 10000
data = []
for i in range(N):
    sample = generate_sample()
    if sample["train"] == "delayed":
        data.append(sample["appointment"])
print(Counter(data))
result
1
2
3
4
python .\sample.py
	Counter({'attend': 1321, 'miss': 868})
python .\sample.py
	Counter({'attend': 1244, 'miss': 867})
Likelihood Weighting 可能性加權
1
2
3
- Start by fixing the values for evidence variables.
- Sample the non-evidence variables using conditional probabilities in the Bayesian network.
- Weight each sample by its likelihood: the probability of all the evidence occurring.

Markov Model

1
2
3
4
- Markov Assumption 馬卡夫假設
	the assumption that the current state depends on only a finite fixed number of previous states
- Markov Chain
	a sequence of random variables where the distribution of each variable follows the Markov assumption
model.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
from pomegranate import *

# Define starting probabilities
start = DiscreteDistribution({
    "sun": 0.5,
    "rain": 0.5
})

# Define transition model
transitions = ConditionalProbabilityTable([
    ["sun", "sun", 0.8],
    ["sun", "rain", 0.2],
    ["rain", "sun", 0.3],
    ["rain", "rain", 0.7]
], [start])

# Create Markov chain
model = MarkovChain([start, transitions])

# Sample 50 states from chain
print(model.sample(50))
result
1
2
python .\model.py
	['rain', 'sun', 'sun', 'rain', 'rain', 'rain', 'sun', 'sun', 'sun', 'sun', 'sun', 'sun', 'sun', 'rain', 'sun', 'rain', 'rain', 'rain', 'sun', 'sun', 'sun', 'sun', 'sun', 'rain', 'rain', 'rain', 'rain', 'rain', 'sun', 'sun', 'rain', 'rain', 'sun', 'sun', 'rain', 'sun', 'sun', 'sun', 'sun', 'sun', 'sun', 'sun', 'rain', 'rain', 'sun', 'sun', 'sun', 'sun', 'sun', 'sun']

Markov Models #2

1
2
3
4
- Hidden Markov Models
  a Markov model for a system with hidden states that generate some observed event
- Sensor Markov Assumption
	the assumption that the evidence variable depends only the corresponding state
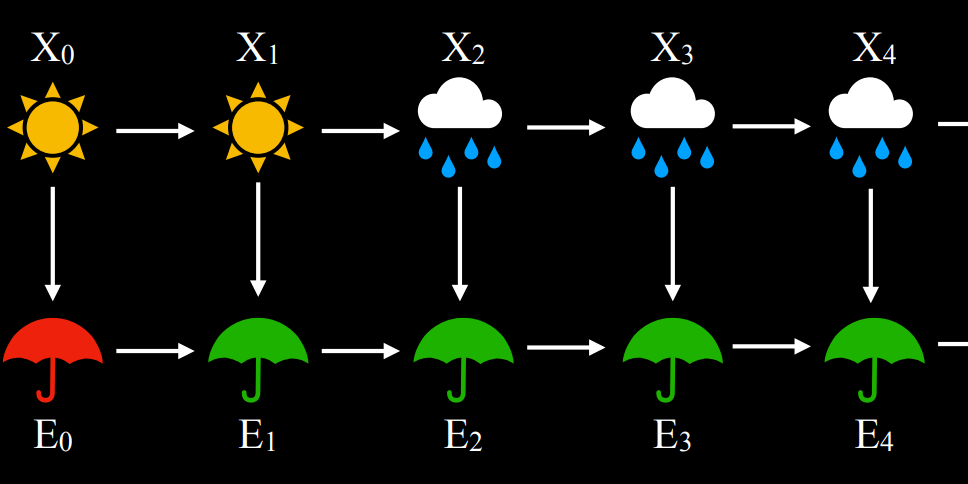
model.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
from pomegranate import *

# Observation model for each state
sun = DiscreteDistribution({
    "umbrella": 0.2,
    "no umbrella": 0.8
})

rain = DiscreteDistribution({
    "umbrella": 0.9,
    "no umbrella": 0.1
})

states = [sun, rain]

# Transition model
transitions = numpy.array(
    [[0.8, 0.2], # Tomorrow's predictions if today = sun
     [0.3, 0.7]] # Tomorrow's predictions if today = rain
)

# Starting probabilities
starts = numpy.array([0.5, 0.5])

# Create the model
model = HiddenMarkovModel.from_matrix(
    transitions, states, starts,
    state_names=["sun", "rain"]
)
model.bake()
sequence.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from model import model

# Observed data
observations = [
    "umbrella",
    "umbrella",
    "no umbrella",
    "umbrella",
    "umbrella",
    "umbrella",
    "umbrella",
    "no umbrella",
    "no umbrella"
]

# Predict underlying states
predictions = model.predict(observations)
for prediction in predictions:
    print(model.states[prediction].name)
result
1
2
3
4
5
6
7
8
9
10
python .\sequence.py
	rain
	rain
	sun
	rain
	rain
	rain
	rain
	sun
	sun

Optimization

Term

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Local search
Hill Climbing

Simulated Annealing

Traveling Salesman Problem

Linear Programming

Constraint Satisfaction

unary constraint 單元
binary constraint 雙元
node consistenc節點一致性 - unary constraint
arc consistency 弧一致性 - 符合 binary constraint

backtracking serach 回溯搜尋

Inference
maintaining arc -consistency

Learning

Term

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
Learning 
	1. Supervised Learning 監督學習 (have label)
	2. reinforcement learning 強化學習
	3. unspervised learnin 無監督學習(no label)

1. Supervised Learning 監督學習
nearest-neighbor classification 鄰近分類
k-nearest-neighbor classification :   k nearest data point  鄰近分類

perceptron learning rule 感知器學習規則

Support Vector Machine 支持向量
maximum margin separator 最大邊距分隔

regression 回歸
Evaluating Hypotheses 評估假設
loss function 

L1 loss function 
L(actial, predicted) = | actual - predicted|
L2 loss function
L(actial, predicted) = (actual - predicted)^2

Overfitting 過度吻合

regularization 正規化
cost(h) = lost(h) + r complexity(h)

holdout cross-validation 保留交叉驗證
k-fold cross validation Y折交叉驗證

python lib: scikit-learn(nearest neighbor)
perceptron  感知機

2. reinforcement learning 強化學習
Markov Decision Process
Q-learning : Q(s,a)
	Q(s, a) <- Q(s, a) + alpha * (new value estimate - old value estimate)

Greedy Decision-Making

Explore vs. Exploit 探索與利用

e-Greedy
Nim game

function approximation

3. unspervised learnin 無監督學習(no label)
Clustering 群聚
 
Some Clustering Applications 一些叢集應用
- Genetic research  基因研究
- image segmentation 影像分割
- market research 市場調查
- medical imaging 醫學影像
- social network analysis 社會網絡分析

k-means clustering

banknotes0.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
import csv
import random

from sklearn import svm
from sklearn.linear_model import Perceptron
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier

# model = Perceptron()
# Results for model Perceptron
# Correct: 541
# Incorrect: 7
# Accuracy: 98.72%

# model = svm.SVC()
# Results for model SVC
# Correct: 545
# Incorrect: 3
# Accuracy: 99.45%

model = KNeighborsClassifier(n_neighbors=1)
# model = KNeighborsClassifier(n_neighbors=1)
# holdout = int(0.40 * len(data))
# Results for model KNeighborsClassifier
# Correct: 548
# Incorrect: 0
# Accuracy: 100.00%

# model = KNeighborsClassifier(n_neighbors=1)
# holdout = int(0.50 * len(data))
# Results for model KNeighborsClassifier
# Correct: 685
# Incorrect: 1
# Accuracy: 99.85%
# can set : model = KNeighborsClassifier(n_neighbors= 3)

# model = GaussianNB()
# Results for model GaussianNB
# Correct: 466
# Incorrect: 82
# Accuracy: 85.04%

# Read data in from file
with open("banknotes.csv") as f:
    reader = csv.reader(f)
    next(reader)

    data = []
    for row in reader:
        data.append({
            "evidence": [float(cell) for cell in row[:4]],
            "label": "Authentic" if row[4] == "0" else "Counterfeit"
        })

# Separate data into training and testing groups
# holdout = int(0.40 * len(data))
holdout = int(0.50 * len(data))
random.shuffle(data)
testing = data[:holdout]
training = data[holdout:]

# Train model on training set
X_training = [row["evidence"] for row in training]
y_training = [row["label"] for row in training]
model.fit(X_training, y_training)

# Make predictions on the testing set
X_testing = [row["evidence"] for row in testing]
y_testing = [row["label"] for row in testing]
predictions = model.predict(X_testing)

# Compute how well we performed
correct = 0
incorrect = 0
total = 0
for actual, predicted in zip(y_testing, predictions):
    total += 1
    if actual == predicted:
        correct += 1
    else:
        incorrect += 1

# Print results
print(f"Results for model {type(model).__name__}")
print(f"Correct: {correct}")
print(f"Incorrect: {incorrect}")
print(f"Accuracy: {100 * correct / total:.2f}%")

banknotes1.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import csv
import random

from sklearn import svm
from sklearn.linear_model import Perceptron
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.neighbors import KNeighborsClassifier

model = Perceptron()
# model = svm.SVC()
# model = KNeighborsClassifier(n_neighbors=1)
# model = GaussianNB()

# Read data in from file
with open("banknotes.csv") as f:
    reader = csv.reader(f)
    next(reader)

    data = []
    for row in reader:
        data.append({
            "evidence": [float(cell) for cell in row[:4]],
            "label": "Authentic" if row[4] == "0" else "Counterfeit"
        })

# Separate data into training and testing groups
evidence = [row["evidence"] for row in data]
labels = [row["label"] for row in data]

# train_test_split 自動分組
X_training, X_testing, y_training, y_testing = train_test_split(
    evidence, labels, test_size=0.4
)

# Fit model
model.fit(X_training, y_training)

# Make predictions on the testing set
predictions = model.predict(X_testing)

# Compute how well we performed
correct = (y_testing == predictions).sum()
incorrect = (y_testing != predictions).sum()
total = len(predictions)

# Print results
print(f"Results for model {type(model).__name__}")
print(f"Correct: {correct}")
print(f"Incorrect: {incorrect}")
print(f"Accuracy: {100 * correct / total:.2f}%")

Neural Networks

Term

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
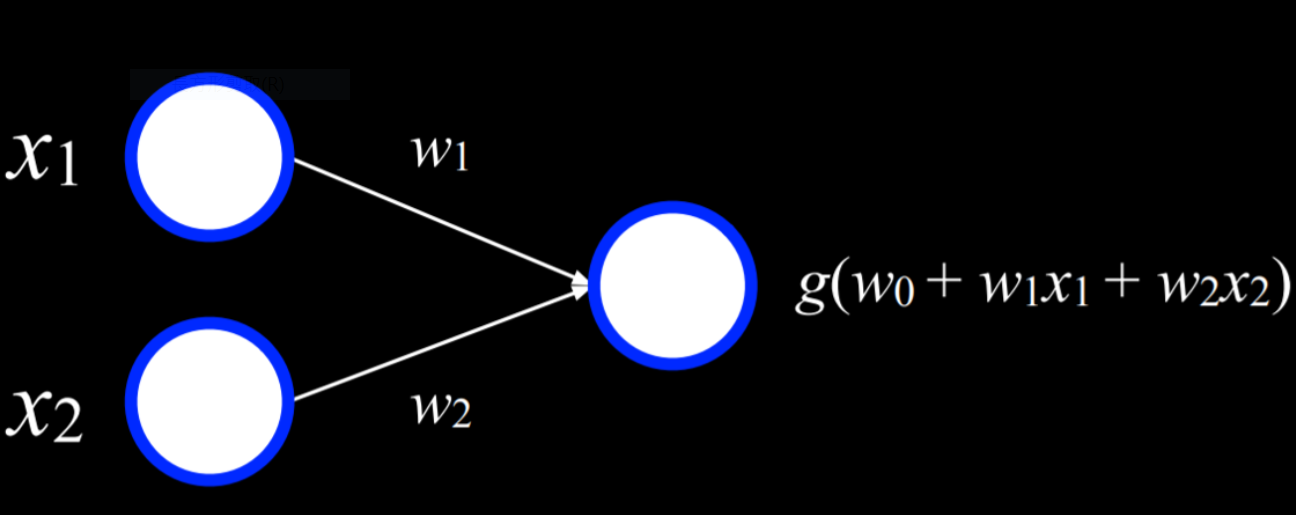
24
artificial neural network(ANN)人工神經網路
gradient descent梯度下降
stochastic gradient descent隨機梯度下降
Mini-batch gradient descent小批量梯度下降
Perceptron 感知器
multilayer neural network多層神經網路
backpropagation 反向傳播
deep neural network深度神經網絡
overfitting 過度擬合

dropout 輟學技術 - random remove some unit

TensorFlow

computer vision 
image convolution 影像卷積(filter)
pooling 池化 - reduce
max-pooling最大值池化

convolutional neural network(CNN) 卷積神經網路
convolution  --> pooling

feed-forward neural network 前饋神經網路
Recurrent Neural Networks 循環神經網路

content

Neural Network Structure
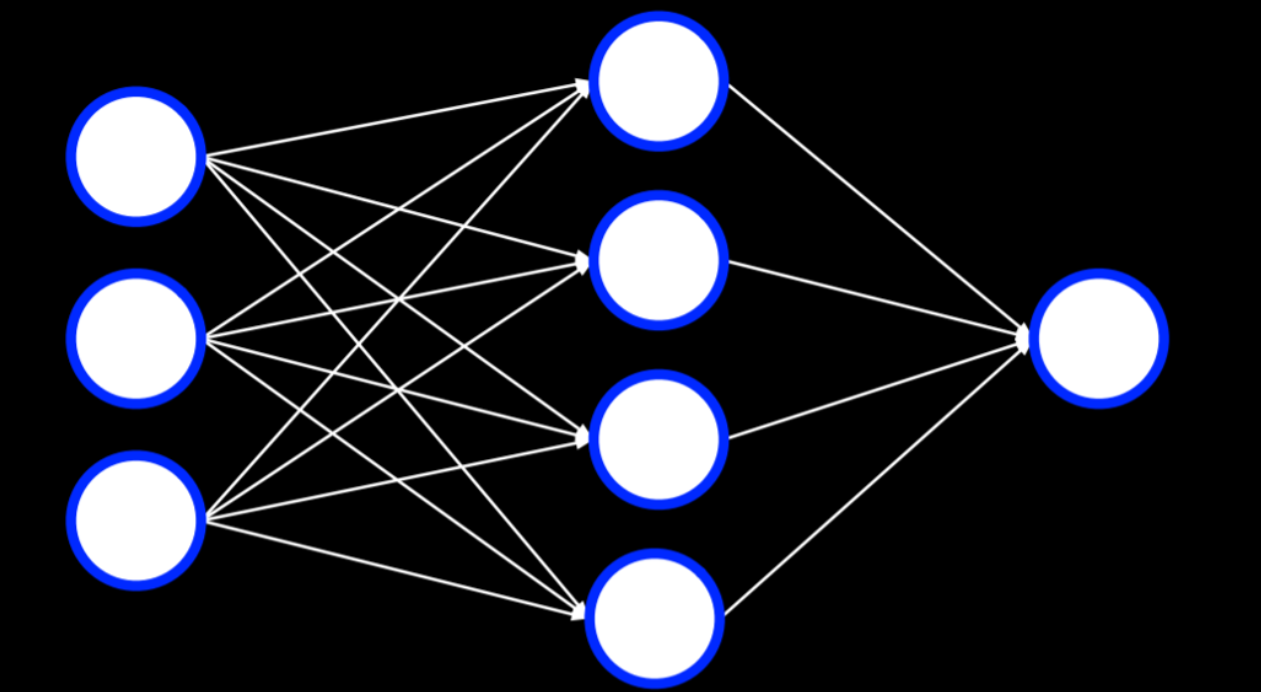
Multilayer Neural Networks
Overfitting
Image Convolution
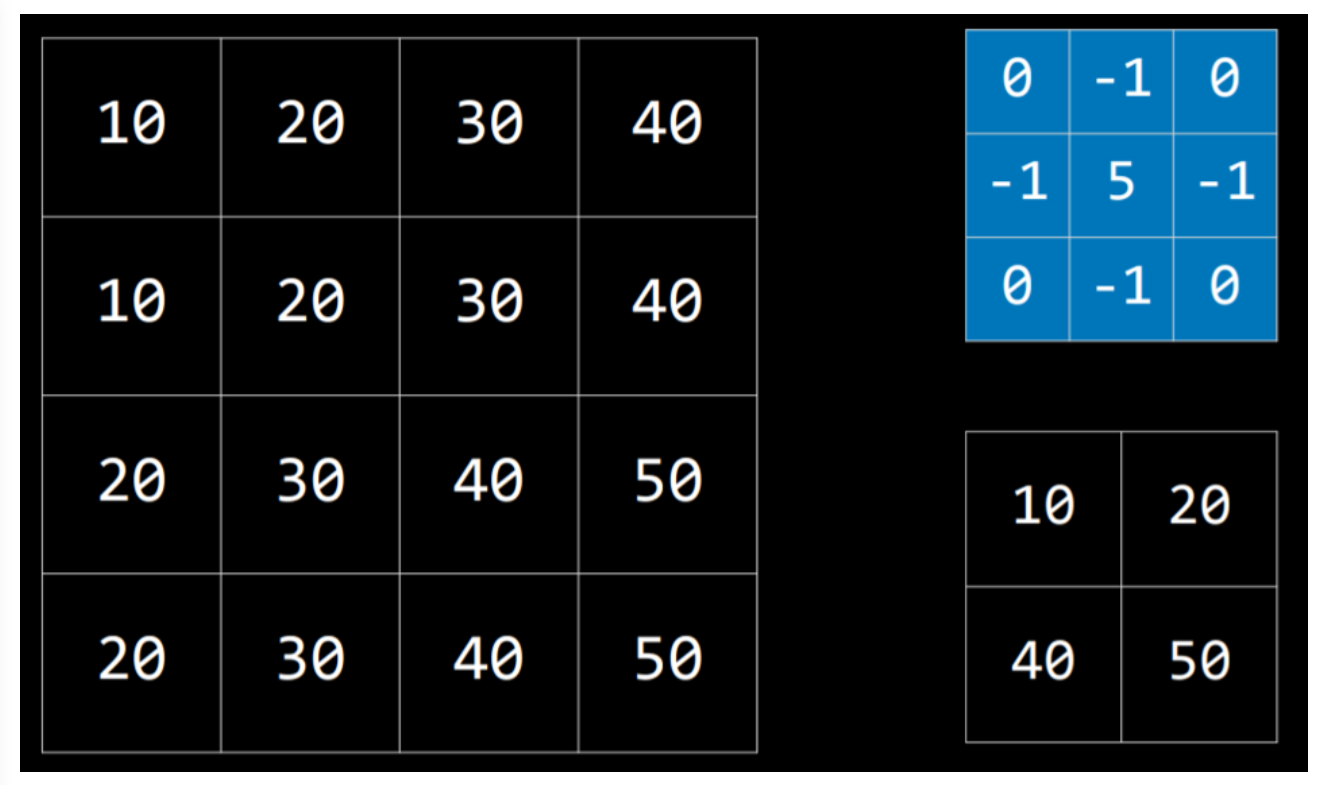
max-pooling
Convolutional Neural Networks
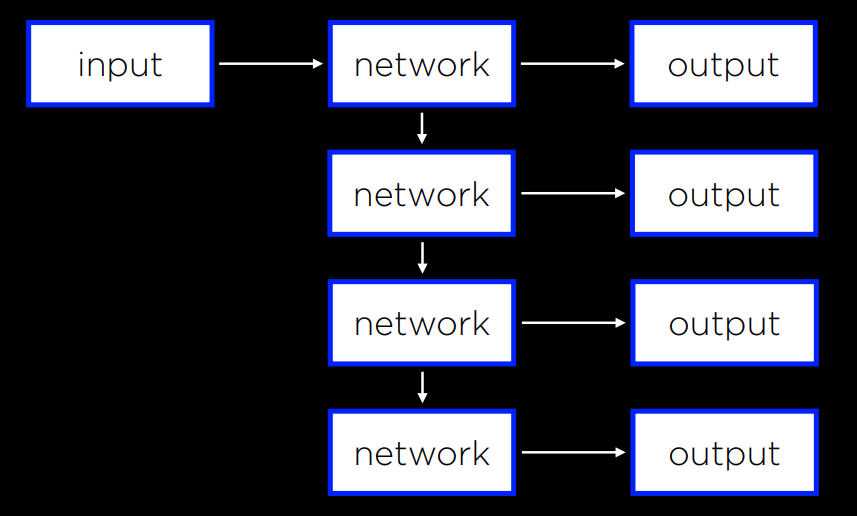
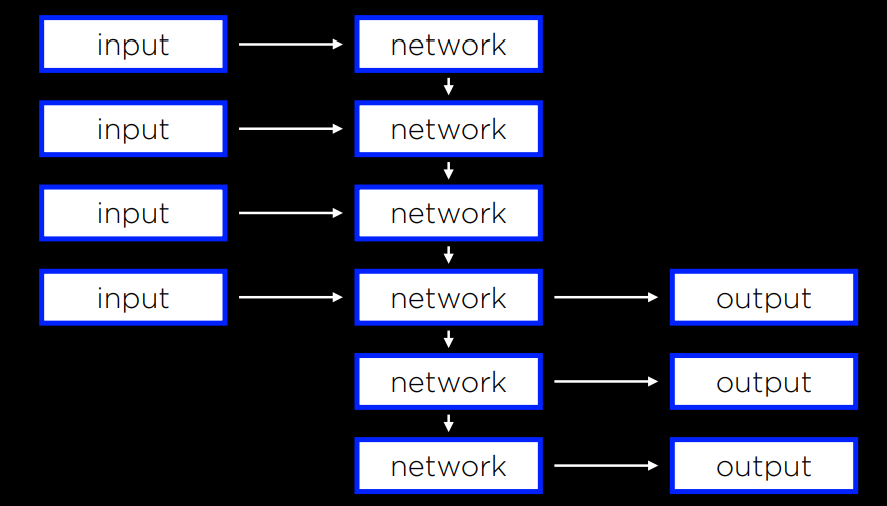
recurrent neural network
CaptionBot
Youtub
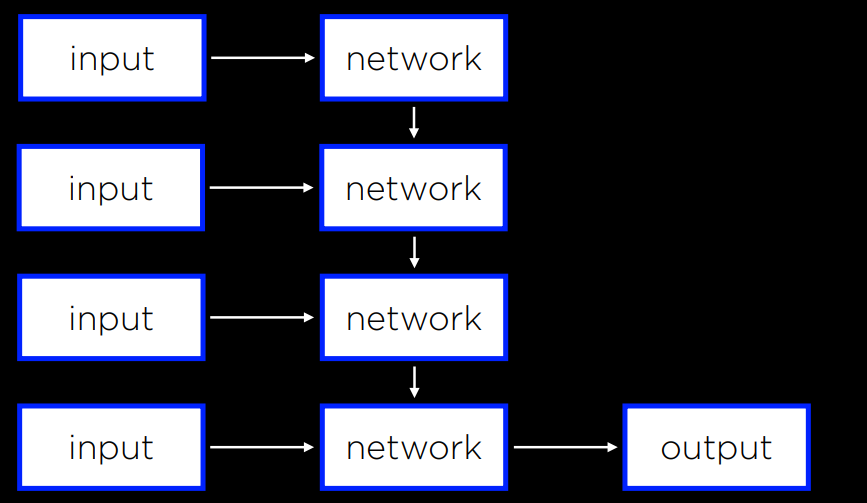
google 翻譯

code

banknotes.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import csv
import tensorflow as tf

from sklearn.model_selection import train_test_split

# Read data in from file
with open("banknotes.csv") as f:
    reader = csv.reader(f)
    next(reader)

    data = []
    for row in reader:
        data.append({
            "evidence": [float(cell) for cell in row[:4]],
            "label": 1 if row[4] == "0" else 0
        })

# Separate data into training and testing groups
evidence = [row["evidence"] for row in data]
labels = [row["label"] for row in data]
X_training, X_testing, y_training, y_testing = train_test_split(
    evidence, labels, test_size=0.4
)

# Create a neural network
# models : one API
# Sequential : 多層
model = tf.keras.models.Sequential()

# Add a hidden layer with 8 units, with ReLU activation
# 8 : 8 hide unit
# 4 : 4 input data
# relu : active function
model.add(tf.keras.layers.Dense(8, input_shape=(4,), activation="relu"))

# Add output layer with 1 unit, with sigmoid activation
# 1 : 1 output
model.add(tf.keras.layers.Dense(1, activation="sigmoid"))

# Train neural network
# optimizer="adam" :　select optimizer model
# loss="binary_crossentropy" : select loss model
# metrics=["accuracy"] : 評估準確性
model.compile(
    optimizer="adam",
    loss="binary_crossentropy",
    metrics=["accuracy"]
)
# training 20 times
model.fit(X_training, y_training, epochs=20)

# Evaluate how well model performs
model.evaluate(X_testing, y_testing, verbose=2)
filter.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import math
import sys

from PIL import Image, ImageFilter

# Ensure correct usage
if len(sys.argv) != 2:
    sys.exit("Usage: python filter.py filename")

# Open image
image = Image.open(sys.argv[1]).convert("RGB")

# Filter image according to edge detection kernel
# 3*3 Kernel for filter
filtered = image.filter(ImageFilter.Kernel(
    size=(3, 3),
    kernel=[-1, -1, -1, -1, 8, -1, -1, -1, -1],
    scale=1
))

# Show resulting image
filtered.show()
handwriting.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
import sys
import tensorflow as tf

# Use MNIST handwriting dataset
mnist = tf.keras.datasets.mnist

# Prepare data for training
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
y_train = tf.keras.utils.to_categorical(y_train)
y_test = tf.keras.utils.to_categorical(y_test)
x_train = x_train.reshape(
    x_train.shape[0], x_train.shape[1], x_train.shape[2], 1
)
x_test = x_test.reshape(
    x_test.shape[0], x_test.shape[1], x_test.shape[2], 1
)

# Create a convolutional neural network
model = tf.keras.models.Sequential([

    # Convolutional layer. Learn 32 filters using a 3x3 kernel
    tf.keras.layers.Conv2D(
        32, (3, 3), activation="relu", input_shape=(28, 28, 1)
    ),

    # Max-pooling layer, using 2x2 pool size
    tf.keras.layers.MaxPooling2D(pool_size=(2, 2)),

    # Flatten units
    tf.keras.layers.Flatten(),

    # Add a hidden layer with dropout
    tf.keras.layers.Dense(128, activation="relu"),
    # 刪掉一半
    tf.keras.layers.Dropout(0.5),

    # Add an output layer with output units for all 10 digits
    tf.keras.layers.Dense(10, activation="softmax")
])

# Train neural network
model.compile(
    optimizer="adam",
    loss="categorical_crossentropy",
    metrics=["accuracy"]
)
model.fit(x_train, y_train, epochs=10)

# Evaluate neural network performance
model.evaluate(x_test,  y_test, verbose=2)

# Save model to file
if len(sys.argv) == 2:
    filename = sys.argv[1]
    model.save(filename)
    print(f"Model saved to {filename}.")

Python

setup

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# check which python 
python -c "import sys; print(sys.executable)"
	D:\app\Python310\python.exe

# chick install package 
pip3 list  
	Package            Version
	------------------ ------------
	apricot-select     0.6.1
	attrs              20.3.0
	....
	
# change env for python
# run by cmd
D:\app\python_env\myenv11_01\Scripts\activate.bat

package

list
1
2
3
4
5
6
7
8
9
10
# SciPy Python : 演算法庫和數學工具包
pip3 install scipy
# python-constraint : 實現對有限域上處理 CSPs（(Constraint Solving Problems -約束求解問題）的支持
pip3 install python-constraint
# scikit-learn : Scikit-learn是用於Python程式語言的自由軟體機器學習庫。它包含了各種分類、回歸和聚類算法，包括多層感知器、支持向量機、隨機森林、梯度提升、k-平均聚類和DBSCAN，它被設計協同於Python數值庫NumPy和和科學庫SciPy。
pip3 install scikit-learn
# TensorFlow : 是一個開源軟體庫，用於各種感知和語言理解任務的機器學習。目前廣泛地用於研究和生產中，比如Google商業產品，如語音辨識、Gmail、Google 相簿和搜尋
pip3 install tensorflow

pip3 install pygame
csv
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
import csv

evidence = []
labels = []
with open(filename) as f:
    reader = csv.reader(f)
		# jump 1st row
    next(reader)

    for row in reader:
        evidence.append([
            int(row[0]),
            float(row[1]),
            int(row[2]),
            float(row[3]),
            int(row[4]),
            float(row[5]),
            float(row[6]),
            float(row[7]),
            float(row[8]),
            float(row[9]),
            abbreviated_month_to_int(row[10]),
            int(row[11]),
            int(row[12]),
            int(row[13]),
            int(row[14]),
            1 if row[15] == 'Returning_Visitor' else 0,
            1 if row[16] == 'TRUE' else 0,
        ])
        labels.append(1 if row[-1] == 'TRUE' else 0)

syntax

anonymous functions
1
2
testGreedy(foods, maxUnits,
           lambda x: 1/Food.getCost(x))
1
2
3
4
5
6
7
8
9
10
11
12
13
>>> f1 = lambda x: x
>>> f1(2)
2

>>> f2 = lambda x,y: x + y
>>> f2("Jery", "Tom")
'JeryTom'

>>> f3 = lambda x,y: 'factor' if (x%y ==0) else 'not factor'
>>> f3(4,2)
'factor'
>>> f3(4,3) 
'not factor'
class print function : string
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Food(object):
    def __init__(self, n, v, w):
        self.name = n
        self.value = v
        self.calories = w
    def getValue(self):
        return self.value
    def getCost(self):
        return self.calories
    def density(self):
        return self.getValue()/self.getCost()
    def __str__(self):
        return self.name + ': <' + str(self.value)\
                 + ', ' + str(self.calories) + '>'
@classmethod
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class MyClass:
    class_variable = "I am a class variable"

    def __init__(self, instance_variable):
        self.instance_variable = instance_variable

    # Regular instance method
    def instance_method(self):
        print(f"Instance method called with instance variable: {self.instance_variable}")

    # Class method decorated with @classmethod
    @classmethod
    def class_method(cls):
        print(f"Class method called with class variable: {cls.class_variable}")

# Creating an instance of MyClass
obj = MyClass("I am an instance variable")

# Calling the instance method
obj.instance_method()

# Calling the class method
MyClass.class_method()

# class_method is a class method decorated with @classmethod. It can only access class variables, not instance variables. The first parameter, conventionally named cls, refers to the class itself.
dict - key by tuple
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
self.q = dict()
self.q[tuple(state), action] = new_q

def get_q_value(self, state, action):
    """
    Return the Q-value for the state `state` and the action `action`.
    If no Q-value exists yet in `self.q`, return 0.
    """
    try:
        return self.q[tuple(state), action]
    except KeyError:
        return 0

# other exception
for move in moves:
    try:
        q = self.q[tuple(state), move]
    except:
        q = 0

function

sorted
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def buildMenu(names, values, calories):
    """names, values, calories lists of same length.
       name a list of strings
       values and calories lists of numbers
       returns list of Foods"""
    menu = []
    for i in range(len(values)):
        item = Food(names[i], values[i], calories[i])
        menu.append(Food(names[i], values[i],
                          calories[i]))
    return menu

def greedy(items, maxCost, keyFunction):
    itemsCopy = sorted(items, key = keyFunction,
                       reverse = True)


names = ['wine', 'beer', 'pizza', 'burger', 'fries',
         'cola', 'apple', 'donut', 'cake']
values = [89,90,95,100,90,79,50,10]
calories = [123,154,258,354,365,150,95,195]
foods = buildMenu(names, values, calories)
testGreedy(foods, 1000, Food.getValue)
zip
1
2
3
4
5
6
7
8
9
10
# example 
a = ("John", "Charles", "Mike")
b = ("Jenny", "Christy", "Monica")
x = zip(a, b)
print(tuple(x))
# (('John', 'Jenny'), ('Charles', 'Christy'), ('Mike', 'Monica'))

# run
for actual, predicted in zip(y_testing, predictions):
    ....
copy
1
2
# copy to new variable
state = game.piles.copy()

items

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# self.q.items() returns a view of the dictionary's key-value pairs,
class MyClass:
    def __init__(self):
        # Assume self.q is a dictionary
        self.q = {'key1': 'value1', 'key2': 'value2', 'key3': 'value3'}

    def iterate_dictionary(self):
        # Using .items() to iterate over keys and values
        for key, value in self.q.items():
            print(f'Key: {key}, Value: {value}')

# Creating an instance of MyClass
obj = MyClass()

# Calling the method to iterate over the dictionary
obj.iterate_dictionary()

tuple - list –> tuple

1
q = self.q[tuple(state), move]

Ref